Matematyka 2 B3

422 VI. Elementy \iuiysiyki niaic/nulu znrj

Gdy dysponujemy próbką (x,.x₂.....x₀) cechy X, to statystyki

G,iG_: w (5 1) przyjmują wartości

g, =h|(x„x₂.....x_n:ct), g₂^sM^xi-^x2.....x_n;u);

wówczas przedział liczbowy (g,,g_:) nazywa się realizacją przedziału ufności (5.1) albo zaobserwowanym przedziałem ufności (5.1).

Współczynnik ufności dotyczy bezpośrednio przedziału ufności (G,,G_?). Nie można natomiast pisać P(g,<0<g_:)=l-a. Powstaje wobec tego pytanie o interpretację współczynnika ufności 1 a w odniesieniu do realizacji (g,,g₂) Odpowiedzi należy szukać w czystościowej interpretacji pr-stwa zdarzenia Otóż. gdybyśmy pobrali 100 n-elementowych próbek i dla każdej z nich wyznaczyli realizację    przedziału ufności (G,.G_:) ze współczynnikiem ufności np.

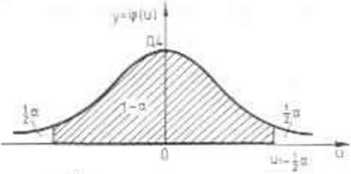
1-a =0,95 oraz każdorazowo twierdzili, że realizacja pokrywa parametr 0, to należy oczekiwać, że 95 razy będziemy mieć rację Na rysunku 5.1 zaznaczono tylko 10 realizacji, z których jedna nie pukrywa parametru 0

*-»i -

Rys 5.1.    Rys 5.2.

Przedziały ufności dla wartości oczekiwanej. Zakładamy, że istnieją wartość oczekiwana p=EX i wariancja

o²=VarX cechy X Przedziałów ufności (G,,G_:) spełniających warunek (5.1) jest nieskończenie wiele. W poniższych tw ierdzeniach będą to najkrótsze przedziały ufności o środku X. a zatem najlepsze przedziały ufności (gdyż EX = p ).

TWIERDZENIE 5.1 Jeżeli cecha X ma rozkład normalny N(u.ct) o znanym odchyleniu standardowym a , to przedział

(5.2)    (X-u _u -?*, X+u _Q -?=)

¹ i vn ¹2 vn

jest przedziałem ufności ze współczynnikiem ufności l-a dla wartości oczekiwanej p; X oznacza lu średnią arylmctyczną PLP (X,,X_2r...Xj cechy X, liczba u,__n,_: jest kwantylem rzędu p = ł-a/2 ZL U o rozkładzie N(0; I).

Dowód. Standardowe postępowanie przy wyznaczaniu przedziałów ufności polega na następujących czynnościach.

I) Wprowadzamy do rozważań "statystykę wyjściową", zależną od estymowunego parametru, której rozkład jednak nie zależy od tego parametru. W naszym przypadku jest to statystyka:

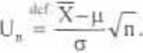
2)    Wyznaczamy rozkład pr-stwa tej statystyki. Przy założeniach twierdzenia średnia arytmetyczna X ma rozkład normalny N(p,a/Vn), (por tw 13). ZL U„ jest zestundaryzowaną ZL X, ma więc rozkład normalny N((J;ł).

3)    Dobieramy liczby a i b tak. aby

P(a < ———Vn < b) = l-a. a

Liczby te można wybrać na dowolną liczbę sposobów Przedział będzie najkrótszy, jeśli a u_a/2=-U|__a/: oraz b= u,(por. rys 5.2):

P(-u „ <<^u. J = i-<*-

• , CJ    ¹ i

4)    Przekształcając tożsamość i owo nierówność podwójną występującą po lewej stronie ostatniej równości, otrzymujemy:

I'(X-u „ -9- < M < X₊u „ -^) = l-a. ^lml Vn    '"T vn

Zgodnie z definicją przedziału ufności, równość ta uzasadnia nazwanie przedziału (5.2) - przedziałem ufności zc współczynnikiem ufności !-a dla wartości oczekiwanej p.    11

PRZYKŁAD 5.1. Niech X oznacza zużycie przędzy na wyprodukowanie jednego metra bieżącego tkaniny płaszczowej. Dokonano n=9 niezależnych, jednakowo dokładnych pomiarów i otrzymano wy niki