skan0033

'-I'

czyli rozwiązanie w\ ma posiać:

Wi

-fi-1		-r
fi	, lub wi =	0
4/3 + 1		1

dla fi =s 0.

■-1'		‘-I’		te-i'
1	+ e*	0	=	t
4		.1		4t +1 _

Stąd wynilca, że odpowiednie rozwiązanie ui jest określone wzorem ua = te^tx^ + e^twy = te*

Należy teraz rozwiązać pierwsze dwa równania z układu (2.10.9). Rozwiązując^ drugie równanie z (2.10.9), mamy

1 i 0	-2		1	1	0 :	-2		1	1	0 :	-2
0 -4 1	2	~	0	-4	1 :	2		0	-4-	1 :	2
.-1 -13 3	8.		.0	-12	3 :	6.		.0	0	0 :	0:

ceyll

‘-7-21    r-2‘

W\ =    7    , lub W\ —    0 dla 7 = 0.

47 +2 J    2

Jego rozwiązaniem. Podobnie, dla pierwszego równania z (2.10.9) mamy

1	1	0 i	-2		1	1	0	-2		1	1	0 :	-2
0	-4	1 :	0		0	-4	1	0		0	-4	1 :	0
.-1	-13	3 :	2.		.0	-12	3	0.		.0	0	0 :	0.

a stąd wynilca, że rozwiązanie ma postać

	-e - 2		'-2'
xua =	e 4c	, lub W2 =	0 0

dla e = 0.

Zgodnie /, wcześniejszymi oznaczeniami, mamy

*-l' 1	+ *<8*	'-2' 0	||	‘-2’ 0		'-t^a -2i ■ 2 i^8
4		2		0		4# «l 2#

Zauważmy, że IbBWl^K&nlft ni,U'j l ^w3 są liniowo niezależne, gdyż rząd macierzy jest równy 3, co pokazują poniższe rachunki:

(	‘-1 1 —t^2 -2t — 2	V (\
r (	1 t t^2	=^r
1	4 4t + l 4t^2+2t	1 i

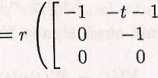
-t² -2t-2 —2t — 2

-t² -2t- 2 —2t — 2 —6t — 8

= 3.

Z powyższych rozważań wynika, że szukane rozwiązanie jest określone następująco:

y(t) = CiUi(t) + C2U2(t) + CiUz(t)

	'-1'		'-t-l'		’ -t^2 -2t-2
Cie^ł	■ -j* 4	+ C2e^4	t 4t +1	|c3e*	t^2 4t^2 + 2t

2.10.2. Metoda uzmiennienia stałych

Powróćmy do równania niejednorodnego (2.10.2). Załóżmy, że znane jest rozwiązanie ogólne

2/0(t) — CiUi(t) + CzU2{t) H-----h CnUnit)

równania jednorodnego (2.10.4). Rozwiązanie to można również zapisać w postaci

yo{t) = X(t)C,    (2.10.10)

gdzie X jest macierzą kwadratową stopnia n, której kolumny są wektorami postaci ui(t),U2(t)y“ •    oraz C = [Ci CV • • • C_n]^T. Macierz X nazywa się ma

cierzą fundamentalną naszego układu. Ponieważ wektory kolumnowe macierzy X są liniowo niezależne, to stąd wynika, że X jest macierzą nieosobliwą, czyli istnieje macierz odwrotna X“¹ w pewnym otwartym przedziale. Pochodną funkcji macierzowej X otrzymujemy poprzoz różniczkowanie każdej funkcji wewnętrznej X, a więc

■ X'(t)C oraz X'{t)C ■ AX{t)C_{