0026

27

§ 4. Dalsze własności i zastosowania liczb rzeczywistych

Łatwo zauważyć, że klasy te nie są puste oraz że X zawiera także liczby dodatnie.

Jeśli wziąć np. liczbę naturalną m tak, żeby było — <a<m, to także jest    < a <m",

m    m

czyli liczba l/m należy do X, a liczba m do X'.

Dalsze wymogi co do przekroju sprawdzamy bezpośrednio.

Niech teraz £ będzie liczbą określoną przekrojem X\X'; pokażemy, że £"=a, tj. że ę=Z/a. Traktując £" jako iloczyn n czynników równych na podstawie definicji iloczynu dodatnich liczb rzeczywistych [14] wnosimy, że

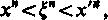
jeżeli x i x' są dodatnimi liczbami wymiernymi, dla których

0<x<^<x'.

Ponieważ oczywiście x należy do klasy X, a x' do klasy X', to z definicji tych klas mamy jednocześnie    _

Ale różnica x'—x może być uczyniona mniejszą niż dowolna liczba e>0 (uwaga z ustępu 9), przy czym możemy przyjąć, że x' jest mniejsze niż pewna najpierw ustalona liczba x'₀. W takim przypadku różnica spełnia nierówność

x"^,—xⁿ=(x'—x)(x"‘~¹+x-x'ⁿ~² + ...+xⁿ~¹)<e-nx'o~ⁱ,

tj. można ją uczynić dowolnie małąC¹). Stąd według lematu 2 wynika równość liczb C i a.

Skoro udowodniono istnienie pierwiastka, w zwykły sposób ustala się pojęcie potęgi o dowolnym wykładniku wymiernym r, i sprawdza się, że potęgi takie spełniają zwykłe reguły, przytaczane w podręcznikach algebry elementarnej:

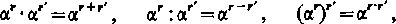
Zauważmy jeszcze, że dla a> 1 potęga oc^r rośnie wraz ze wzrostem wykładnika wymiernego r.

19. Potęga o dowolnym wykładniku rzeczywistym. Przejdźmy do określenia potęgi dowolnej rzeczywistej (dodatniej) liczby a o dowolnym wykładniku rzeczywistym fi. Rozważmy potęgi liczby a

tx^b i a^b

o wymiernych wykładnikach b i b’, spełniających nierówności

b<P<b’.

O Zauważmy, że liczba e • nx'₀ⁿ~¹ jest mniejsza niż dowolna liczba e'> 0, jeśli obierzemy e < —7^—

nx₀