0524

525

Zagadnienie przedłużania funkcji

Przyjmiemy wobec tego następującą umowę. Gdy będziemy mówili o pochodnej cząstkowej pewnego typu ciągłej w obszarze Jt, to w przypadku punktu M₀ leżącego na brzegu będziemy przez tę pochodną rozumieli granicę, do której dąży pochodna tego typu w punkcie wewnętrznym M, gdy M dąży do M₀ (¹). Umowa ta będzie obowiązywać niezależnie od tego, czy ta wartość -graniczna pochodnej będzie rzeczywiście pochodną, czy nie.

Z dalszego wykładu stanie się jasne, że ta wartość graniczna dla szerokiej klasy przypadków jest zarazem naprawdę pochodną, jeżeli tylko położenie punktu M₀ względem obszaru pozwala w ogóle mówić o pochodnej rozpatrywanego typu. Dla najprostszego przypadku obszaru prostokątnego wykażemy to zresztą już teraz.

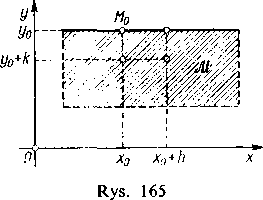
Niech zatem funkcja /(x, y) będzie ciągła wraz ze swoimi pochodnymi aż do rzędu n włącznie («> 1) w pewnym prostokącie .4/. i niech punkt M₀(xo, }'₀) leży na odcinku prostej y=y₀ będącym brzegiem tego prostokąta i należącym do niego (rys. 165).

Dla pochodnej/^ zagadnienie rozstrzyga się łatwo. Według wzoru Lagrange’a [112] stosunek przyrostów wynosi

f(x₀,y₀ + k)-f(x₀,y₀) k

=fy(x₀, y₀ + 9k)

(O<0<1).

Dla k-^0 stosunek ten dąży zatem do wartości granicznej f'_y(x₀, y₀), która jest tym samym także pochodną w zwykłym sensie (porównaj ustęp 113). Dla pochodnej f'_x sam stosunek przyrostów może być rozpatrywany jako granica

f(x₀ + h, y₀)-f(x₀, y₀) f(x₀ + h, y₀ + k)-f(x₀, y₀ + k)

------= lim------.

h    n-o    h

Wyrażeniu, którego granicę trzeba obliczyć, możemy nadać następującą postać, stosując twierdzenie Lagrange’a:

f(x o + h,y₀ + k) -f(x o ,y₀ + k) k

=fx(x_o + 0h, y₀ + k)

(O<0<1).

Gdy /j->0 i k-¹0, wyrażenie to dąży do wartości granicznej f'_x{x₀, y₀). Na podstawie twierdzenia z ustępu 168 ta podwójna granica jest równa granicy iterowanej, bo istnieje granica pojedyncza dla k-¹0. Zatem

fx(x₀, ko) = l™^lim

h->0 k-¹0

f(x₀ + h,y₀ + k)-f(x₀ ,y₀ + k) _ h

= lim

h^+O

f(x₀ + h, y₀)-f(x₀, y₀) h

1

Zachowamy przy tym dla tej pochodnej zwykłe oznaczenie.