0248

1

00

250

XI. Szeregi nieskończone o wyrazach stałych

Szereg

a-l

(<r>0) jest zbieżny wraz z szeregiem

2‘-

1

2*u+«>

X

Szereg £ 1-0

1

n In «

jest rozbieżny, gdyż jest rozbieżny szereg

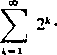
1

2* In 2^Ł

X

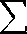
k-1

itd.

W twierdzeniu tym można zastąpić szereg^ 2^ka₁t służący do porównania przez ogólniejszy szereg

00

£    gdzie m jest dowolną liczbą naturalną.

3) Niech (A) będzie dowolnym szeregiem zbieżnym. Co można wnosić o rzędzie małości o„ w stosunku do 1 /«?

Przede wszystkim jest oczywiste, że jeśli wielkości te są ze sobą w ogóle porównywalne [60], tzn. jeśli istnieje granica

lim

a.

Mn

lim na_n = c ,

to musi być koniecznie c — 0, czyli

(13)    o, = o ^ .

Rzeczywiście, w przeciwnym razie — wobec rozbieżności szeregu harmonicznego — dany szereg byłby także rozbieżny [366, twierdzenie 2].

Na ogół jednak granica taka nie musi istnieć, jak widać na przykładzie szeregu

■ + — + — H— --1- ...

8²    9    10²

Zbieżność tego szeregu jest widoczna z porównania z szeregiem    —r ■ Tymczasem, jeżeli n nie jest

n«l **

pełnym kwadratem, to dla niego jest na„ = 1/n; w przeciwnym razie na„ = 1.

Zresztą jeżeli wyrazy szeregu maleją monotonicznie, to warunek (13) jest jednak konieczny dla zbieżności szeregu. Rzeczywiście dla dowolnych m i n>m jest

(n — m) u„ <    + ... +a„ < a,„ ,

gdzie y,„ jest resztą szeregu. Stąd

na„ < ---a,„.

n—m

Weźmy najpierw m tak duże, by było mniejsze od dowolnie przyjętej liczby «>0. Jeżeli założymy teraz, że ;i jest takie duże, że

n

n — m

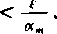
to jest jednocześnie na,<e, c.b.d.o.