0427

429

§ 4. Dodatkowe wiadomości o szeregach potęgowych

stronie nie może być zbieżny dla .v = ±7t i tym bardziej dla |jt| >7t. Promień zbieżności szeregu jest dokładnie równy 7t(‘).

Stąd między innymi jest oczywiste, że taki sam promień zbieżności będzie miał szereg (13), podczas gdy szereg wyjściowy (12) ma promień zbieżności 2n.

Korzystając z tożsamości

tg x = ctg Ar- 2 ctg 2a:

i stosując (15), łatwo można na nowo otrzymać rozwinięcie

(16)

tg -v =

OD

s

2^ł,(2^ł"—1) (2«)!

B„x²

Jest ono równoważne z otrzymanym wcześniej wzorem [patrz (11)], lecz najczęściej używana jest ta jego postać, ponieważ liczby Bernoulliego są dobrze zbadane i istnieją obszerne tablice tych liczb. Promień zbieżności szeregu przedstawiającego tg x jest równy tt/2, co widać już teraz z samego sposobu otrzymywania tego szeregu.

Z liczbami Bernoulliego związane są także inne pożyteczne rozwinięcia. Na przykład, ponieważ

(ln

sin x

cos x sin x

x

— (*ctg x— 1) = —

X

£

H-l

2 ²"B_n

(2 «)!

_v2łl — J

ł

więc całkując wyraz za wyrazem otrzymujemy (dla |jcl <tt)

ln iii* ₌ _ V" 2²"B, . x^_

" .*    Zj (2/7)!    2/i '

K»> 1

Analogicznie, z rozwinięcia (16) po scałkowaniu otrzymujemy (dla [a] <tc/2)

ln cos Ar

n-i

2²"(2²"-l )B„ (2//)!

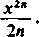
tR X

Z tych rozwinięć łatwo otrzymamy rozwinięcie ln —— . Z szeregów tych korzysta się przy sporządzaniu

tablic logarytmów funkcji trygonometrycznych.

Powróćmy na zakończenie do szeregu rozbieżnego

£ (-1)"(«+1)\ n= 0

który rozpatrywaliśmy w zadaniu 6) ustępu 425. Tam ustaliliśmy sumowalność tego szeregu metodą Ce-sary rzędu k, lecz samej sumy uogólnionej (oznaczamy ją przez /ś^(k>)nie otrzymaliśmy; zrobimy to teraz. Zresztą obliczymy tę sumę metodą Poissona-Abela, co jak wiemy [424, 2)], powinno dać ten sam wynik. Dla / >0 mamy 0<e~'<l i obliczając sumę szeregu otrzymujemy

V (_])» _ri.d)i ₌ f¹ _ i ₌ _J___2_₌ 1 . _L___L . ^2t

„    l—e-t e' — l e’ — l e²' — l t e‘ — l t e²' — 1

n-0

(*) Nawiasem mówiąc wszystkie zagadnienia dotyczące wyznaczenia promienia zbieżności szeregu potęgowego łatwo dają się rozwiązać, gdy skorzystamy z twierdzenia Cauchy’ego-Hadamarda [380], Na przykład w przypadku szeregu (15) mamy;

P,,-. - 0, _P2B = 5/gŁ =    . _J2„ ₌ ± ^

\ (2/0! V (2 /;)!    (27t)²ⁿ    tt ^r

R

lim p„, = — ,