1954 Geometria 040

Pritom yyrok ,,utvary sa neprekryvaju“ ma vel’mi jednoduchy vy-znam, ked ide o obdlżniky a śtvorce, a znamena, że obidva utvary móżu mat spolocnu najviac iba ćast obvodov.

rn^r'><r>

Priklad 4. Mamę dokazat, że vzorec pre obsah obdlżnika P = ab plati i y pripade, że niektóry z rozmerov a, b alebo obidva su cisla iraeionalne; napr. a = 5 cm, 6 = |/3 cm.

Riesenie. Podia tabulky je

1,73 < |/3 < 1,74.

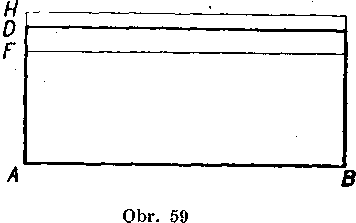
Zostrojime obdlżniky ABCD, ABEF a ABGH (obr. 59) s rozmermi a = AB = 5 cm, 6₁ = BE = 1,73 cm, b — BG = |/3 cm, b₂ = BG = = 1,74 cm.

Podia ylastnosti (6) pre obsahy obd!żnikov plati:

ABCD = ABEF + FECD, ABGH = ABCD + DCGH,

preto

ABEF < ABCD < ABGH.

Pretoże rozmery obd!żnikov ABEF, ABGH su racionalne cisla, su ich obsahy (v cm²)

ABEF = 5.1,73; ABGH = 5.1,74.

Pre obsah obdlżnika ABCD teda plati

5.1,73 < ABCD < 5.1,74.

Móżeme vśak vyjsf a j zo vztahov

1,732 < ]/3 < 1,733;

potom rovnakou uvahou ako predtym dójdeme ku vzfahom

5.1,732 < ABCD < 5.1,733.

Takymto sposobom dostaneme dalśie nerovnosti, napr.

5.1,732 05 < ABCD < 5.1,732 06

atd. Ż algebry viete, źe jedine cislo, które vyhovuje vsetkym tymto vztahom, je ćislo 5.]/3. Preto

ABCD = 5.1/3,

co sme chceli dokazat.

Priklad 5. Mamo dokazat, ze Yzorec pre obsah trojuholnika P = | av plati aj v tom pripade, ked’ vel’kosti strany a a Yyśky v su vyjadrene luboYoiiiymi realnymi ćislami (aj iracionalnymi). Mamę Yykonat dokaż napr. pre ostrouhły trojuholnik ABC, ak a — BC =

= yi3, v_m = y7.,

Riesenie (obr. 60). Zo- f    A    D

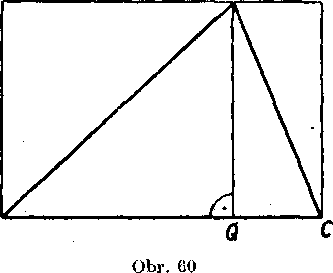
strojime v trojuholniku ABC vyśku AQ; pata vysky Q padnę na usecku BC, pre-toże obidva uhly <£ ABC a <XBOA su ostre. Trojuhol-nikMBCsaskladaz trojuhol-nikov ABQ, ACQ, które sa.

,.neprekryvaju", preto pre jeho obsah plati

&.ABC = A ABQ + g

+ A ACQ.

Trojuholniky ABQ, ACQ doplnime na obdlżniky AEBQ, ADCQ (obr. 60). Ich obsahy podia predchadzajuceho prikladu su

AEBQ = BQ. AQ, ADCQ = CQ.AQ.

Podia vety sus o zhodnosti trojuholnikov je vśak

A aeb a a AQB, AADC A a aqc.

Podia vlastnosti (5), (6) pre obsah utvaru plati

AEBQ = 2. A ABQ, ADCQ = 2. A ACQ,

41