MATEMATYKA128

246

V. Całka oznaczona

Chcemy określić pole |D| trapezu krzywoliniowego D lak, aby określenie to było zgodne z intuicyjnym rozumieniem pola figury' płaskiej oraz dostarczyło efektywnego narzędzia obliczania tego pola Postawione zadanie realizujemy za pomocą następującego postępowania, zachowuje przy tym dotychczasowe oznaczenia

Przedział <a,b> dzielimy na n przedziałów częściowych <x_i_,,x_j > o długościach AXj. W każdym przedziale częściowym obieramy dowolny punkt x, i budujemy prostokąty o postawach Ax, i wysokościach h, ss f(Xj). Suma (w sensie dodawania zbiorów) tych n prostokątów tworzy' zakreskowaną na rysunku 1.2 figurę schodkową D„. Niech |D_n| oznacza jej pole. Pole to jest sumą pól rozważanych prostokątów:

l^Dnl=Z^h»^Axi = Z^f^*^)Axi‘-

i=l    i=l

Rozważamy granicę ciągu (|D_n|) pól |D_n| figur schodkowych D„. odpowiadającego normalnemu ciągowi podziałów przedziału <a,b> Wobec założonej ciągłości funkcji f granica ta istnieje i ma tę samą wartość przy każdym normalnym ciągu podziałów' i przy każdym wyborze punktów pośrednich x, w przedziałach częściowych Ze wzrostem n figury schodkowe D_n coraz dokładniej przy legają do trapezu D. Postąpimy więc naturalnie przyjmując następującą definicję.

Niech f będzie funkcją ciągłą i nicujemną na przedziale <a,b>. Polem |D| trapezu krzywoliniowego D={(x,y)eR^:: aśx<,b,0£y£f(x)> nazywamy granicę ciągu (|D_n|) pól |D_n| figur schodkowych D_n, odpowiadającego dowolnie wybranemu normalnemu ciągowi podziałów przedziału <a,b> i dowolnemu wyborowi punktów pośrednich x₍ w przedziałach częściowych tych podziałów: dci'    n

(1.2)    |D|* lim |DJ-- hm YfO^.

n-*»    n->»    ,

(Ą-HJ)    (S,-+ O)¹"¹

b

Ostatni człon równości (1.2) jest całką oznaczoną Jf(x)dx. Mamy

o

zatem następującą interpretację geometry czną całki oznaczonej.

1. Określenie całki oznaczonej i jej interpretacje

247

(1)    Jeśli f jest funkcją ciągłą i tucujemną na przedziale < a, b >, to

b

i alka oznaczona Jf(x)dx jest polem |D| trapezu krzywoliniowego a

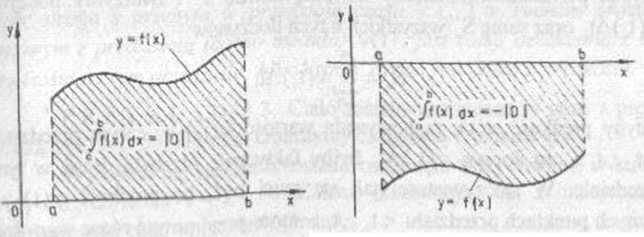
I) {(x,y)eR^z: a£x£b, ()śy£f(x)}, (por rys 1.3):

b

(1.3)    Jf(x)dx =|D|.

a

(2)    Jeśli f jest funkcją ciągłą i niedodatmą na przedziale <a,b >. I) _;{(x,y)eR²:aśxśb. f(x)£y*0}, (por. rys 1.4), to

(14)

jf(x)dx = -|Di.

Rys 1.3    ^1 ⁴

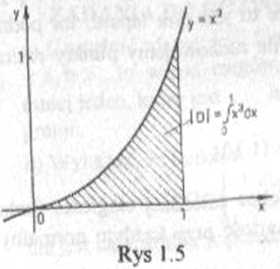
PRZYKł.AD 1.2 Pole figury

»

D^^yJeR^O^kOsy:^}

(rys 15), wyraża się całką :

i

|D|=jx^Jdx

0

Występującą tu całkę oznaczoną, korzystając z definicji , obliczyliśmy w przykładzie 1.1. Zatem |D|= 1/4. ’    ■