83028 PC043366

Rozdział 3. Funkcje jednej zmiennej

Definicja 3.24 obejmuje jedynie przypadek, gdy a < b. Wygodnie jest |$| szerzyć definicję symbolu (3.30) na inne przypadki. Przyjmujemy, że

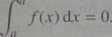
Przykład 3.60.

Pokażemy, że funkcja stała f(x) = o. x e (a,b), jest całkowalna. Suma całkowa (3.28) przyjmuje postać

S(f,P,c) = ,/(ęj)fo - ą-i) = a    .ir/_|.) = a(b - a).

Jej wartość jest niezależna od sposobu podziału i wybieranych punktów c. Jej grania przy Ó(P) -» 0 jest zawsze równa a(b — a). Wymogi całkowalności są zatem spełniona

y «'/(*)

Rys. 3.9. Jeśli funkcja / przyjmuje wartości nieujemne, to suma całkowa jest przybliżeniem pola powierzchni obszaru D Źródło: opracowanie własne

Badanie całkowalności funkcji na podstawie samej definicji jest bardzo uciążliwe, nawet w przypadkach „prostych” funkcji. Na szczęście zachodzi następujący fakt.

Twierdzenie 3.45.

Niech a,b e R, a < b. Jeśli ograniczona funkcja /: (a,b) -* R jest ciągła poza skończoną liczbą punktów, to / jest całkowalna. W szczególności, jeśli / jest ograniczona i monofoniczna na (a, b), to jest tam całkowalna.

Przykład 3.61.

Niech a,b £ R, gdzie a < b. Każda z funkcji: f(x) = |x|, g(x) = sgnx, gdzie x f {a,b), spełnia założenia twierdzenia 3.45, zatem jest całkowalna.

Twierdzenie 3.46.

Załóżmy, że funkcje f,g są całkowalne na przedziale (a,b). Wtedy: a) Dla dowolnych a,fi | R funkcja af + fig jest też całkowalna oraz

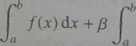
(«/(»> +fig(,x))    = a    g(x) dx.

h) jeśli (c.d) C (a, b). to / Jest całkowalna na (c,d).

_c)    Jeśli c 6 (a,b)_t to £ f(x)óx = £ f(x)dx + £ f(x)dx.

d)    Jeśli wartości funkcji / oraz g są równe poza, być może. skończoną liczbą punktów, to f(x)dx = Jr g(x)d*.

_e)    Jeśli /(.v) < g(x) dla x e (a,b), to /(jc)djc < jf gt*)d*. W szczególności funkcja |/| jest całkowalna i zachodzi nierówność

| /(x)dr| < | |/(x)|d*.

I %Ja    I Ja

Jeśli m < /(*) < M dla x € (a, b>, to

m(b — a) < I f(x) dx < M(b - a).

Twierdzenie 3.47. (Wzór Newtona)

Jeżeli / jest ciągła na przedziale (a, b), to

(3.31)

\f(x) dx - F(b) - F(a),

gdzie F jest dowolną funkcją pierwotną funkcji /.

Uwaga. Różnicę F(f>) - F(a) oznacza się często symbolem F(*)£.

Przykład 3.62.

Obliczymy całki oznaczone wybranych funkcji. Ich funkcje pierwotne wyznaczaliśmy w przykładach 3.35 i 3.36. Mamy:

r/4    J

tgxd.v = In|smx||^ = -ln 2,

J x sin xdx = (—x cos x + sin .r)£ =

Geometryczna interpretacja całki oznaczonej

Niech f:(a,b)—*R będzie funkcją ciągłą o wartościach nieujemnych. Całka £ f(x) dbc jest równa polu powierzchni obszaru

D = {(x, y): x e (a, b), 0 < y < /(*)),

a więc zbioru ograniczonego prostymi x — a, x — b, osią OX oraz wykresem fiinkcjt / (p. rys. 3.10). Uogólnimy ostatni wynik. Niech f,g będą funkcjami ciągłymi na (a, b), spełniającymi warunek g < /. Pole obszaru

{(*,30: * e (a, b), g(x) < y < /(*)}

143