wykład 8

DYNAMIKA

Układy odniesienia poruszające się ruchem jednostajnym prostoliniowym względem absolutnie nieruchomego układu odniesienia, w którym słuszne są podstawowe prawa dynamiki, nazywamy układami Galileusza (bezwładnościowymi, inercjalnymi)

Galileusz przyjmował Ziemię za absolutny układ odniesienia

Kopernik związał ten układ ze słońcem.

W zagadnieniach technicznych przyjmuje się za układ odniesienia Ziemię, czasami Słońce.

PRAWA NEWTONA

Prawo pierwsze.

Każde ciało trwa w spoczynku lub ruchu jednostajnego prostoliniowego, dopóki siły nań działające tego stanu nie zmienią.

Prawo drugie.

Zmiana ilości ruchu (pędu) jest proporcjonalna względem siły działającej i ma kierunek prostej, wzdłuż której ta siła działa.

P V

m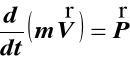
(1)

gdzie mV wektor pędu, m masa,

V wektor prędkości, P wektor siły

Jeśli m = const. to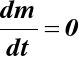
i równanie ( 1) ma postać

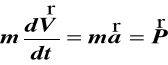
(2)

Prawo trzecie

Każdemu działaniu towarzyszy równe i wprost przeciwne oddziaływanie, czyli wzajemne działanie dwóch ciał są zawsze równe i skierowane przeciwnie.

ciało 1 ciało 2

P₁ P₂ Rys.2 P₁ = - P₂

Prawo czwarte

Jeśli na punkt materialny o masie m działa jednocześnie kilka sił, to każda z nich działa niezależnie od pozostałych, a wszystkie razem działają tak, jak jedna tylko siła równa wektorowej sumie wektorów danych sił.

Prawo czwarte nazwano prawem superpozycji i zapisano

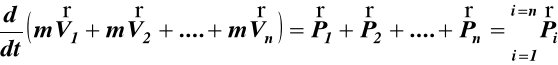
(3)

P₁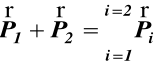

m

P₂ Rys.3

Prawo piąte

Każde dwa punkty materialne przyciągają się wzajemnie z siłą wprost proporcjonalną do iloczynu mas (m₁, m₂) i odwrotnie proporcjonalnie do kwadratu odległości r między nimi. Kierunek siły leży na prostej łączącej te punkty. Prawo to nazywamy prawem grawitacji

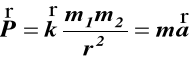
m₁ m₂ (4)

P

r

k stała grawitacji Rys.4

Dynamika swobodnego punktu materialnego

Z drugiego prawa Newtona (1)

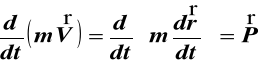
dla m = const.

w prostokątnym układzie współrzędnych mamy

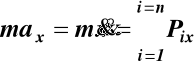
dynamiczne równania różniczkowe

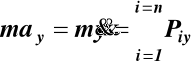
ruchu punktu materialnego w układzie

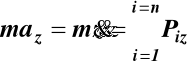
współrzędnych prostokątnych (5)

Przykład 1

Punkt materialny o masie m = 2 kg porusza się po linii prostej określonej równaniem x = t³- 5t²- 12t + 3 m. Wyznaczyć wartość siły działającej na punkt dla t = 1.5 s.

Rozwiązanie

Prędkość i przyśpieszenie punktu wynoszą:

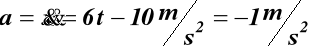
Wartość siły wywołującej ruch punktu

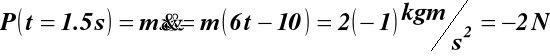
W układzie współrzędnych naturalnych

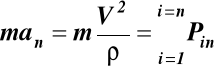
na oś normalną

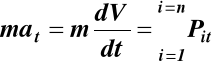
na oś styczną (6)

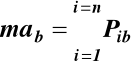
na oś binormalną

Przykład 2

Punkt materialny o masie m = 3.4 kg porusza się po okręgu o promieniu R = 1.1 m zgodnie z równaniem ruchu punktu po torze s = 2m + R(t² + 2t) m. Wyznaczyć wartość siły działającej na punkt jako funkcję czasu oraz wartość tej siły dla t = 3.2 s.

Rozwiązanie

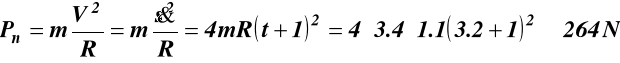
Wartość siły P

P_t

Dynamika nieswobodnego punktu materialnego

Ruch takiego punktu możemy rozpatrywać jako ruch punktu swobodnego pod wpływem sił czynnych P i biernych R. Równanie wektorowe nieswobodnego punktu materialnego o stałej masie m ma postać

(7)

W układzie naturalnym równanie (7) przyjmuje postacie

,

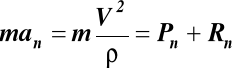
(8)

Przykład 3

Punkt materialny o masie m zsuwa się w dół równi nachylonej do poziomu pod kątem α = 25⁰. Wyznaczyć przyśpieszenie a punktu materialnego w przypadku gdy między powierzchnią równi a zsuwającym się punktem współczynnik tarcia wynosi μ =0.4. Przyśpieszenie ziemskie g = 9.81 m/s².

Rozwiązanie y

N R

0 F m N

x a

F

G =mg α

x

Rys.5 N + F = R

Wzór (7) ma postać ma = G + R

Rzutując siły: na oś x mamy
(a)

na oś y

siła F jest siłą tarcia a więc równa się

(b)

podstawiając (b) do (a) i skracając przez m mamy

Ruch punktu pod działaniem siły stałej co do wartości i kierunku

Z drugiego prawa Newtona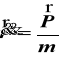

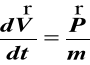
(c)

całkując (c) dwukrotnie otrzymujemy

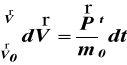
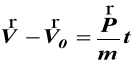
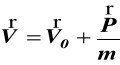
ponieważ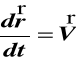

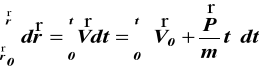
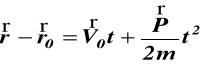
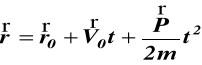
(d)

Przykład 4

Punkt materialny o masie m kg spada pionowo z prędkością początkową V₀ ms^-1. Znaleźć równanie ruchu punktu materialnego jeśli (x)_{t = 0} = x₀, (V_x)_{t = 0} = V₀,

g przyśpieszenie ziemskie

Rozwiązanie 0

P_x = G = mg x₀

Równanie różniczkowe ruchu m

x V₀

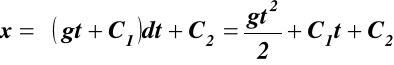
m

po podstawieniu warunków brzegowych G =mg

C₂ = x₀, C₁ = V₀

Rys.7

Otrzymujemy ostatecznie

,
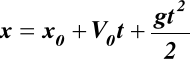
(e)

Ruch punktu pod działaniem siły zależnej od czasu

Równanie (2) ma postać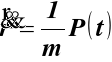
,
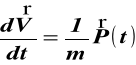
(f)

całkując (f) otrzymamy prędkość V w funkcji czasu

,
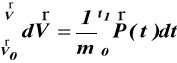
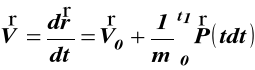
(g)

całkując (g) otrzymamy wektor opisujący położenie punktu r (t)

,
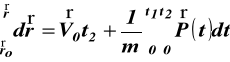
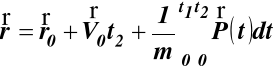
(h)

Przykład 5

Na znajdujący się w spoczynku punkt materialny o masie

m zaczęła w pewnej chwili działać siła P o stałym kierunku i wartości proporcjonalnej do czasu. Należy wyznaczyć równanie ruchu punktu, jeżeli wiadomo, że po upływie czasu t₀ siła osiągnęła wartość równą P₀.

Rozwiązanie

W rozpatrywanym przypadku miara siły P względem osi

0x (rys.8) jest funkcja czasu t. Jeżeli czas będziemy mierzyć od chwili, w której siła zaczęła działać na punkt materialny, to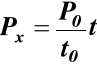

0 m P

x m x Rys.8

Równanie różniczkowe ruchu (f) ma postać

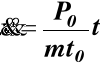
całkując dwukrotnie to równanie znajdujemy

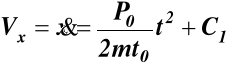
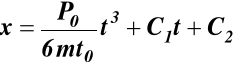
W chwili t = 0 prędkość punktu materialnego była równa zeru. Jeżeli początek 0 osi 0x obierzemy w położeniu początkowym badanego punktu materialnego, to w chwili

t = 0 mamy również x = 0. W rozpatrywanym przypadku muszą być spełnione następujące warunki:

,

Po podstawieniu tych warunków do wyrażeń (i)

C₁ = C₂ = 0

Odpowiedz: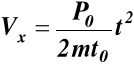
,

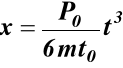
1dyn

2dyn

3dyn

4dyn

R

P_n

5dyn

6dyn

7dyn

(i)

---