CCF20140608003

26 2. Układ iterowanych odwzorowań (IFS)

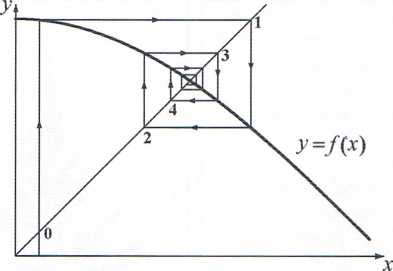
Rys. 2.2. Geometryczna interpretacja zbieżności ciągu rekurencyjnego xq, x\, xi,..., gdzie x_n+1 = f(x„) metrycznych itp). Jeżeli każdej parze elementów X\, x^ jest przyporządkowana liczba nieujemna p(x 1,3:2) w taki sposób, że spełnione są warunki (tzw. aksjomaty metryki)

p(x 1/^2) =0 wtedy i tylko wtedy, gdy x\ = x-i

p(x 1,^2) = p(x2,xi)    - warunek symetrii

p{x\,x2) + p(x2,0:3) ^ p(xi, *3)    - nierówność trójkąta

to funkcjonał p nazywamy metryką, a jego wartość p(x 1,^2) nazywamy odległością między punktami X\ i X2-

Definicja 2.1. Zbiór X wraz z określoną na nim metryką p nazywamy przestrzenią metryczną i oznaczamy przez (X,p).

Mówimy, że ciąg X\, xi, M, elementów przestrzeni metrycznej (X,p) jest ciągiem Cauchy'ego, jeżeli dalekie wyrazy tego ciągu są sobie bliskie

p(x_n,x_m)-> o przy u, m —> 00    (2.6)

Definicja 2.2. Jeśli dla każdego ciągu Cauchy'ego x\, xi, *3,... istnieje w przestrzeni metrycznej (X,p) element x_ęX) taki, że p(x_n, Xoo) —* 0 przy n —> co, to mówimy, że przestrzeń metryczna (X,p) jest zupełna, a Xoo nazywamy granicą tego ciągu.

Na przykład zbiór liczb rzeczywistych z metryką p(x\, ^2) = |Xi — X\ jest przestrzenią zupełną, ale zbiór liczb wymiernych z tą samą metryką nie jest przestrzenią zupełną, bo granica ciągu liczb wymiernych nie musi być liczbą wymierną.

Zbiór wszystkich ciągłych funkcji x(t) określonych dla t € [0,1] i przyjmujących wartości w zbiorze liczb rzeczywistych, z metryką p(x 1,^2) =