456 2

456

12. Rozwiązania zadań

8. (a) c=(a² + b² — lab cos O¹'². c - wyznacza się w przybliżeniu za pomocą twierdzenia Pitagorasa.

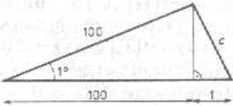
c² = l²+(100-0.01745)² *4.045.

dc _a—bco&C ___ de 6 —ncosC

da c

i . i dc

M^+:ib

-0.49,

*H+

ab

dc

ać

0.51.

c*2.01,

dc ab sin C

dC * 7 '

•M^cl

<0.49 0.1+0.51 -0.1+88-0.01 0.01745<0.12.

(b) Niech cos C=*, gdzie *=0.9998 ±0.5* 10“ *.

c=(a²+b²-2*bx)^ł'^a .

dc

dx

ab _ 100-101

7    2.01

0.5-10*.

?l

|djci<0.5 10⁴ 0.5 10"*=0.25

|^c«*UbljS

skąd |^j<0.37.

(c) cosC=l —2sin² jC=s>c=(a² + b²-2ad+4cbsin²łC)^l/2“(0— Niech sin iC=^, gdzie |dy|<0.5-10^-4.

e*=((a - b)² +4aby²)¹'² ,

175,

dc _4nby 4■ 100-101 0.00873

_r_    2.01

dc

inXMbl\ź\_dy

• |4k|< 175-0.5-10“*<0.009 <0.2-0.12.

Osiągnięto pełną dokładność.

9. (c) *=546.849, j² = 22-10~*.    I M

(d) Dziesięć cyfr. Późniejsze odejmowanie nic obniża dokładności. Informację

się zaokrąglając xf.

(g) " " ‘ Z *<\W-(x-a)(p- P) •

10.    /₇ = [0.0212, 0.0214];    /₈ = [0.0242. 0.0244].

11.    Aby zbadać, w jakiej mierze zależność / od a i b jest liniowa, obliczamy, te

1(0.40 , 0.34) —/(0.39. 0.34)= -0.0266.