65 (94)

3.2. Funkcja kwadratowa

3.2.5. Równania stopnia drug

| a) Wprowadzenie. Wzór funkcji liniowej: y = ax + b można traktować jako równanie stopnia pierwszego (zmienne występują w co najwyżej potędze pierwszej) z dwiema niewiadomymi x i y. Wykresem funkcji liniowej jest prosta, więc związek y = ax + b nazywa się równaniem prostej. Równanie prostej można przekształcić do postaci: Af + By + C — 0.

Analogicznie, wzór funkcji kwadratowej v = ax' + bx + c (a 0 ) jest przykładem równania stopnia drugiego (jedna ze zmiennych występuje w co najwyżej drugiej potędze) z dwiema niewiadomymi x iy. Wykresem funkcji kwadratowej jest parabola, więc związek y = ar' + bx + c nazywa się równaniem paraboli, a parabolę — krzywą stopnia drugiego.

b)    Definicja. Ogólnie równanie stopnia drugiego z dwiema niewiadomymi .v i y jest to równanie postaci: Ar² + Bxy + Cy² + Dx + Ey + F = 0, gdzie A.B.C.D.E.D e R oraz A²+B²+C²# 0 (czyli przynajmniej jeden ze współczynników A, B, C jest różny od zera).

Obraz graficzny tego równania to krzywa stopnia drugiego.

c)    Przy kłady niektórych równań drugiego stopnia Ax²+ Cy²+ F= 0;B = D = E=0

Ar' + Dx + Ey + F=0;B = C = 0 Cy² + Dx = O, A - B = E = F = 0 Bxy + F= 0;A = C = D = E=0

d)    Rozwiązanie równania stopnia drugiego z dwiema niewiadomymi jest to każda para liczb ( x; y ) spełniająca to równanie. Graficznie są to punkty o współrzędnych (x;y) należące do krzywej stopnia drugiego.

e)    Obrazem graficznym zbioru rozwiązań równania drugiego stopnia z dwiema niewiadomymi mogą być na przykład (patrz tabela obok).

Uwaga: Zbiorem rozwiązań równania stopnia drugiego z dwiema niewiadomymi może być zbiór pusty, na przykład równanie x² + y²+ 4 = 0 nie ma rozwiązania.

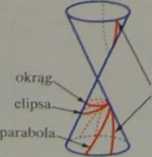
f)    Krzywe stożkowe można otrzymać na powierzchni stożkowej wskutek przecięcia jej płaszczyznami różnic nachylonymi do osi tej powierzchni:

iego z dwiema niewiadomymi

Nazwa

krzywej

Postać równania stopnia drugiego z dwiema niewiadomymi

Obraz graficzny rozwiązania

Parabola

Okrąg

Elipsa

Hiperbola

y = ax~ + bx + c (równanie ma nieskończenie wiele rozwiązań)

x = ay + by + c (równanie ma nieskończenie wiele rozwiązań)

x + y — 2 ax — -2by + c = 0 (równanie ma nieskończenie wiele rozwiązań)

*- + Z_ ₌ i a b a,b>0,a*b (równanie ma nieskończenie wiele rozwiązań)

2 ,2 *» a b a, b > 0 (równanie ma nieskończenie wiele rozwiązań)

xy = k,k^0 (równanie ma nieskończenie wiele rozwiązań)

jO

3. WIELOMIANY I FUNKCJE WYMIER

hiperbola (dwie gałęzie)

Suma prostych (przecinających się

V

pokrywających się)

(a.j + fc.y + c,) • (_aix + b,y + c,) = (równanie ma nieskończenie wiele rozwiązań)

(ax+by+c)²=0 (równanie ma nieskończenie wiele rozwiązań)

Punkt

0(0; 0)

a: +y = 0 (równanie ma jedno rozwiązanie * = o, y = 0)