(RYSUNEK)

Przykład:

dane:

dla

dla

dla

dla

dla
(ostatnia kolumna)

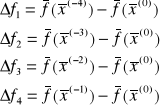
(ostatnia kolumna)

Macierze
i
muszą być nieosobliwe.

Zbieżność ciągu
do
wymaga dostatecznie silnej osobliwości wszystkich macierzy
, czyli:

stała

odpowiednio zmodyfikowana macierz

(modyfikację pomijamy)

sens:
ma istotnie różnić się od 0.

Uwaga:

1. Metoda (n+1)-punktowa - do wyznaczania kolejnego punktu w ciągu
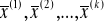
   potrzeba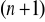
   poprzednich punktów i wartości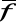
   w tych punktach.

2. Jeśli
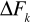
   jest osobliwa to inaczej dobieramy punkty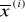
   np. korzystając lokalnie z dyskretnej metody Newtona.

UKŁADY RÓWNAŃ LINIOWYCH

1. metody dokładne (np. wzory Cramera)

2. metody iteracyjne

Układy równań z macierzą trójkątną:

(1)

.............................................

Algorytm podstawiania wstecz dla

Wzór rekurencyjny:

(2)

dla

dla wyznaczenia x :

mnożeń i dzieleń

dodawań

(liczba działań, jak przy znanej macierzy odwrotnej)

Metoda eliminacji Gaussa:

Etap 1

Sprowadzenie do macierzy trójkątnej (A - macierz pełna, nieosobliwa)

Dany:

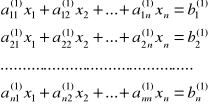
(3)

odejmuję od i-tego wiersza
, wiersz pierwszy pomnożony przez

.....................................

eliminuję z wierszy

po
eliminacjach otrzymamy układ trójkątny górny

Etap 2

Rozwiązujemy układ trójkątny górny stosując wzory (2)

Ilość działań:

mnożeń i dzieleń

dodawań

Bez porównania mniej działań niż wyznaczanie wzorami Cramera.

Przykład:

(był jakiś mętny, pisany na tablicy i nie mam go w całości więc nie zamieszczam, by nie wprowadzać zbędnego zamieszania)

Rozkład LU

A - macierz kwadratowa

Poszukujemy macierzy trójkątnych L i U takich, aby
.

Metoda Gaussa umożliwia:

Zauważmy przekształcenie (
do
)
pomnożeniu obu stron układu (3) przez macierz
.

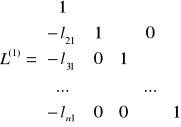
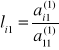
czyli:

następnie:

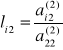
a więc:

macierz trójkątna górna

macierze
,gdzie
- nieosobliwe

a więc:

L

Dzięki specyficznej postaci

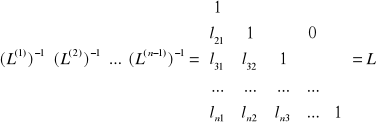
macierz trójkątna dolna

zatem

Mogą istnieć macierze nieosobliwe, których nie da się rozłożyć na
.

---