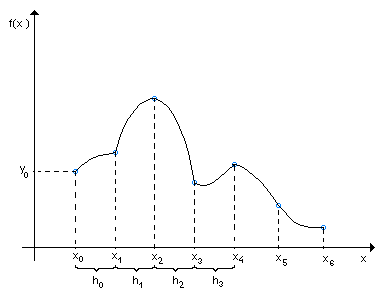
INTERPOLACJA FUNKCJAMI SKLEJANYMI:

- ilość węzłów

- N - ty węzeł

s - układ punktów
dzielących przedział
na N - części

W każdym
przybliżamy f wielomianem ustalonego (niskiego) stopnia, tak aby funkcja przybliżająca była ciągła wraz z pochodnymi na odcinku
.

DEFINICJA

Funkcję rzeczywistą s nazywamy sklejaną (spline) stopnia m z węzłami

jeśli:

1. w każdym przedziale
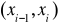
   dla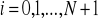
   

s jest wielomianem stopnia nie wyższego niż m

2. s i jej pochodne rzędu
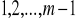
   są ciągłe na całej osi rzeczywistej;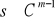
   

dla m = 1 - łamana

wielomiany są szczególnym przypadkiem funkcji sklejanych

Wyznaczanie funkcji sklejanych:

Na każdym
;

jest wielomianem stopnia co najwyżej m

;

Mamy
dowolnych stałych

Żądanie ciągłości pochodnych
w każdym węźle wewnętrznym
;
daje
warunków.

Czyli
zależy od parametrów

wartości funkcji

(NIE JEDNOZNACZNE !!!)

DEFINICJA

Funkcją sklejaną stopnia
nazywamy naturalną, jeśli w przedziałach
dana jest wielomianem stopnia
.

TWIERDZENIE:

Jeżeli węzły
są różne dla
oraz
, to dla dowolnych wartości
istnieje dokładnie jedna naturalna funkcja sklejana
interpolująca punkty
, tzn.
.

Funkcja sklejana okresowa - jednoznaczność interpolacji:

DEFINICJA

Funkcją sklejaną s stopnia m nazywamy okresową o okresie
jeśli
dla
.

Klasę funkcji sklejanych stopnia m z węzłami
oznaczamy
okresowych
naturalnych stopnia
.

Wykazano: (TWIERDZENIE)

Interpolacyjna naturalna funkcja sklejana jest „najgładszą” funkcją interpolującą punktu

Gładkość:

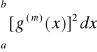
osiąga minimum w klasie funkcji g interpolujących punktu
i takich, że
, a
jest przedziałami ciągła.

przykład:

Wyznacz naturalną funkcję interpolującą, sklejaną stopnia 3 tzn.

w węzłach s

...............................

W każdym z podprzedziałów:

(1)

gdzie:
dla
;

współczynnik
:

bo dla
,
trzeba jeszcze wyznaczyć
współczynników

Korzystamy z warunków, że:

mają być ciągłe w węzłach
dla
otrzymujemy stąd
równań

brakujące warunki otrzymamy z założenia, że s jest funkcją naturalną

Z ciągłości
w węzłach

mamy równość:

gdzie
,

koniec poprzedniego przedziału

w następnym punkcie
gdzie
zaś
, a więc:

(3)

Z ciągłości funkcji s w punkcie
i warunku interpolacyjnego
dostajemy dla
:

(4)

(5)

Z ciągłości
w węzłach

otrzymujemy:

(6)

Podstawiając w miejsce
oraz
zależność (5) oraz (3) po przekształceniu otrzymujemy:

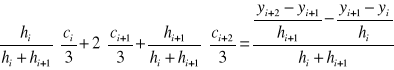
Jeśli szukana funkcja jest funkcją naturalną, to:

---