2048738914

Twierdzenie 4. Rozwiązanie równania stanu (4la) z warunkami brzegowymi (47) ma postać

i+/łi-l    j+n 2-1

⁼    "i^- yi

(48)

(49)

(50a)

(50b)

fc=0    i=0

t+/ti—ii+#t2-i

+    ^2 Ti-k-\j-i-\Buki,

fc=0 J=0

gdzie

£=[& E₂],    «!€R“’,

a macierze tranzycji opisane są zależnościami

Too = In

Tpq = 0    dla p > —/zi, p 7^ 0 oraz q> P2, 9^0

T_pq = 0 (macierz zerowa) dla q < p\ oraz/lub q < P2

T„ = [E₁ 0 ]    c_ai(k)T_P-k,_q-i^j

+ [ 0 E₂ ] ^Tp-l_tq+ *22 ^Ca₂Wp-_hq-}j ~ AT_p_i,₉-dla p > —pi oraz q > —p2-

Zauważmy, że do wyznaczenia wartości wektorów stanu xx\- w dowolnym obszarze 0 < i < N\ oraz 0 < j < N2 (N\, 7V₂ € Z+) wymagana jest znajomość wartości warunków brzegowych oraz wymuszenia spoza tego obszaru, tj. Xqj, x^viQ oraz u# z obszaru 0 < i < N\ + pi — 1 oraz 0 < j < N2 + p.2 — 1.

Przykład 3. (ciąg dalszy Przykładu 1) Weźmy pod uwagę dwuwymiarowy układ ciągły (16) o niecałkowitych rzędach aą = 0.8, ot2 = 0.4 oraz danych macierzach (22).

W wyniku dyskretyzacji układu ciągłego, korzystając z (43), otrzymujemy dyskretny dwuwymiarowy układ niecałkowitego rzędu (41) o macierzach

E =	hf*	K^0A'	, A =	12'
	0	0		0 1
C =	1 0 0 1	, D	= [0],

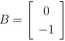
przy czym h\, h₂ są odpowiednio małymi krokami dyskretyzacji.

20

(51)