MIARY EFEKTYWNOŚCI OBLICZEŃ RÓWNOLEGŁYCH
Efektywność zależy od:
- wielkości problemu obliczeniowego
- użytego algorytmu (podobnie jak w obliczeniach rekurencyjnych)
- liczby procesorów
- modelu programowania (model z pamięcią wspólną lub rozproszoną)
- rodzaju architektury
n - wielkość zadania (albo liczba instrukcji albo rozmiar danych)
p - liczba procesorów
T(n,p) - czas wykonania programu realizującego ten sam algorytm dla zadania o wielkości n na komputerze o liczbie procesorów p
S(n,p) - przyspieszenie realizacji zadania o wielkości n dzięki zrównolegleniu na p procesorach
S(n,p) = T(n,1)/T(n,p) <= p
S(n,p) = p , gdy zadanie można podzielić na dokładnie p różnych zadań i przydzielić je do dokładnie p procesorów
procesor p
n
nie da się tego zrównoleglić
dla jednego procesora dla p procesorów
część sekwencyjna część równoległa
ts tr nic nie zrównoleglamy ts tr
T(n,1) ts tr/p
czas wykonania części równoległej
S(n,p) = (ts+tr) / (ts+tr/p)
ts = f(n)T(n,1)
tr = (1-f(n))T(n,1)
S(n,p) = 1 / (f(n)+(1-f(n) / p)) = p / (1+(p-1)f(n)) Prawo Amdahla
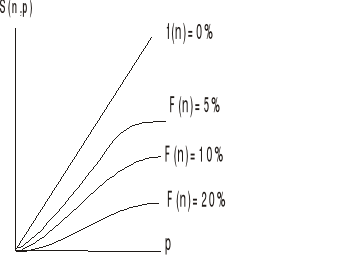
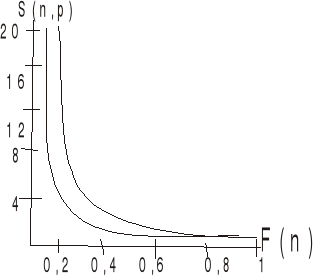
limS(n,p)=1/f(n)
Ułamek stanowiący o części sekwencyjnej decyduje o przyspieszeniu.
Żeby przyspieszenie było duże ułamek musi być bardzo mały.
WYDAJNOŚĆ - stosunek przyspieszenia rzeczywistego do przyspieszenia idealnego
η(n,p) = S(n,p)/p
KOSZT OBLICZEŃ = czas obliczeń * liczba użytych procesorów
Koszt obl. Sekwencyjnych = T(n,1)
Koszt obl. Równoległych = T(n,p)*p = (T(n,1)/S(n,p))*p = T(n,1)/ η(n,p)
SKALOWALNOŚĆ - własność systemu (sprzętu i oprogramowania) polegająca na elastycznym dostosowaniu się do zwiększonej liczby procesorów tzn. na zachowaniu w przybliżeniu tej samej wydajności systemu (η)
η(n,p) = S(n,p)/p = 1 / (1+(p-1)f(n))
Wydajność maleje jeżeli nie zmieniamy n a rośnie p.
FUNKCJA STAŁEJ SKALOWALNOŚCI FISO
- jest miara skalowalności systemu
- podaje jaki musi być rozmiar zadania żeby wydajność była taka sama
FISO
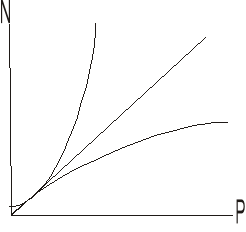
KOMPUTERY MACIERZOWE
Klasa SIMD
Procesor macierzowy=array processor
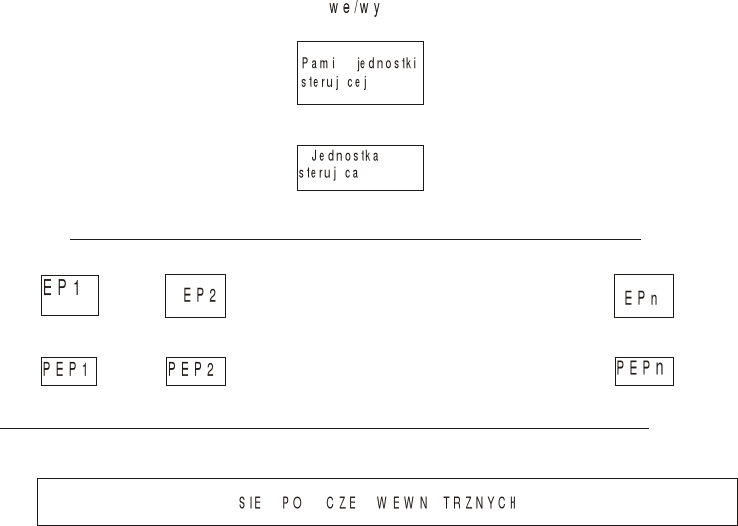
PRZYKŁADY ALGORYTMÓW REALIZOWANYCH W PROCESORACH MACIERZOWYCH
1. Algorytm wyznaczania ciągu sum
for i:=0 to n do A[i+1]:=B[i]+A[i]
A[1]:=B[0]+A[0]
A[2]:=B[1]+A[1] czyli A[2]:=B[0]+B[1]+A[0]
A[3]:=B[0]+B[1]+B[2]+A[0]
A[n+1]:=B[0]+…..+B[n]+A[0]
Sk = Σ B[i]
Wyznaczanie ciągu sum w procesorze macierzowym
EP0 B[0] 0 0 0 S[0]
EP1 B[1] 0+1 0+1 0+1 S[1]
EP2 B[2] 1+2 0+2 0+2 S[2] np. 2+5=2+3+4+5
EP3 B[3] 2+3 0+3 0+3 S[3] złożoność 0(n) / 0(logn) czyli log2
EP4 B[4] 3+4 1+4 0+4 S[4]
EP5 B[5] 4+5 2+5 0+5 S[5]
EP6 B[6] 5+6 3+6 0+6 S[6]
EP7 B[7] 6+7 4+7 0+7 S[7]
Krok 1 krok 2 krok 3
2. Algorytm sortowania bąbelkowego
9 7 4 1 0 -2
-2 9 7 4 1 0 C=(n(n-1))/2
-2 0 9 7 4 1
-2 0 1 9 7 4 C2n=(n2)
-2 0 1 4 9 7
-2 0 1 4 7 9
Elementy przetwarzające
EP0 EP1 EP2 EP3 EP4 EP5
1) 9 7 4 1 0 -2
2) 9 4 7 0 1 -2
3) 4 9 0 7 -2 1
4) 4 0 9 -2 7 1 kroki sortowania
5) 0 4 -2 9 1 7
6) 0 -2 4 1 9 7 połączenie aktywne
0 -2 1 4 7 9
wynik końcowy
Ułamek, część sekwencyjna algorytmu
Jest to 20 krotne przyspieszenie
Dla p=256
Dla p=24
Lepsza skalowalność
Magistrala sterowania
Magistrala danych
Wyszukiwarka
Podobne podstrony:
Przetwarzanie Równoległe i Rozproszczone Szczerbińskiego, wykład 3, SIEĆ PRZETASOWANA (perfect shuff
Przetwarzanie Równoległe i Rozproszczone Szczerbińskiego, wykład 5, PROGRAMOWANIE SYSTEMÓW WIELOPROC
Przetwarzanie Równoległe i Rozproszczone Szczerbińskiego, wykład 2, GRANULACJA PROCESÓW
wyklad 4, przetwarzanie rownolegle i rozproszone - Szczerbinski
wykład 4, przetwarzanie rownolegle i rozproszone - Szczerbinski
[tomko] Progr Rozpr Pytania egzaminacyjne, przetwarzanie rownolegle i rozproszone - Szczerbinski
przyklady na egzamin, szkola, przetwarzanie rownolegle i rozproszone - Prof Szczerbinski
[ tycjan ] - PRIR zadania, szkola, przetwarzanie rownolegle i rozproszone - Prof Szczerbinski
Teoria, przetwarzanie rownolegle i rozproszone - Szczerbinski
[mycek] szczerba, przetwarzanie rownolegle i rozproszone - Szczerbinski
Wyk ad 8 sciaga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
Wyk ad 1 sciaga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
Wyk ad 4 sciĄga, Studia - Automatyka, Przetwarzanie równoległe i rozproszone, egzamin, ściąga
więcej podobnych podstron