AGH, Wydział EAIiE KATEDRA METROLOGII |
Imiona, nazwiska 1. Piotr Bajorowicz 2. Karol Łukiewicz 3. Łukasz Tyrcha |
||
LABORATORIUM METROLOGII |
Semestr: 2 |
||
Rok szkolny 2007/2008 |
Rok studiów: I |
Grupa studencka: 3 |
|
Kierunek: Elektronika i Telekomunikacja |
Zespół: B |
||
Temat ćwiczenia: Zastosowanie pomiarowe oscyloskopu: Pomiary, czasu, częstotliwości, fazy i obserwacja charakterystyk statycznych |
Numer ćwiczenia: 7 |
||
Data wykonania ćwiczenia: 12.04.2008 |
Data zaliczenia sprawozdania |
||
Przygotowanie oscyloskopu do pomiaru
-skompensowanie sondy pomiarowej
Sonda RC o tłumieniu 1:10
a) schemat ideowy;
b) układ zastępczy słuszny dla małych i średnich częstotliwości
Wierne przeniesienie impulsu wymaga równomiernej charakterystyki częstotliwościowej dzielnika R1, C1 i R2, Cz, co występuje wtedy, kiedy jest spełniony warunek R1C1 =R2 Cz.
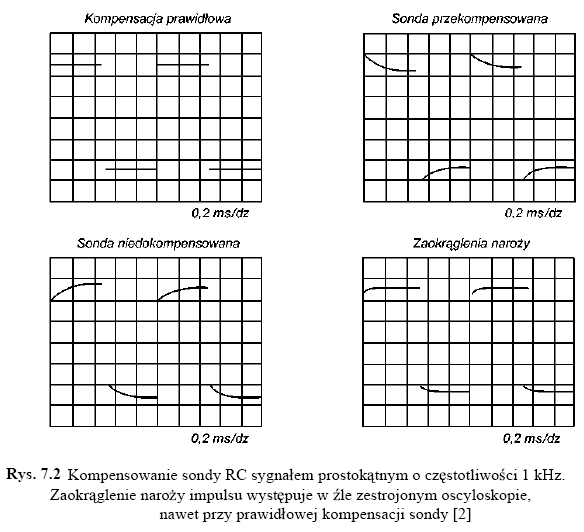
Ponieważ pojemność zastępcza Cz nie jest ściśle określona, to skompensowanie dzielnika uzyskuje się przez strojenie pojemności C1. Sondę stroi się, doprowadzając do jej wejścia sygnał prostokątny z generatora impulsów lub własnego kalibratora oscyloskopu.
Mimo prawidłowej kompensacji sondy na początku impulsu otrzymaliśmy lekkie zafalowania, podobne jak na zamieszczonej ilustracji. Mogło być ono spowodowane złą kompensacją wewnętrznych układów toru Y albo zawilgoceniem elementów czoła sondy.
Pomiar częstotliwości i okresu przebiegów okresowych
za pomocą oscyloskopu
- pomiar metodą bezpośrednią
Układ do pomiaru częstotliwości za pomocą oscyloskopu metodą bezpośrednią,
W metodzie tej częstotliwość fx (lub okres Tx ) wyznaczane są na podstawie
zależności
![]()
gdzie:
lx - długość odcinka na ekranie odpowiadająca okresowi przebiegu Tx ,
Ctx - aktualnie nastawiona wartość stałej podstawy czasu
Pomiary |
Obliczenia |
|||||
|
lx |
Ctx |
fx [Hz] |
Δfx [Hz] |
Tx |
ΔTx |
f1 |
5,7 |
20 μs |
8 771,93 |
±307,79 |
114 μs |
±4 μs |
f2 |
6,8 |
50 μs |
2 941,18 |
±86,51 |
340 μs |
±10 μs |
f3 |
6,9 |
0,1ms |
1 449,28 |
±42,01 |
0,69 ms |
±0,02 ms |
f4 |
7,1 |
0,2 ms |
704,23 |
±19,84 |
1,42 ms |
±0,04 ms |
Błąd pomiaru okresu oraz częstotliwości tej metody można wyznaczyć z prawa przenoszenia błędu:
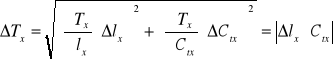
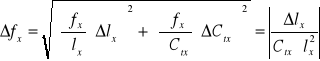
gdzie: ΔCtx - ponieważ nie ustaliliśmy poprawki dla wartości stałej podstawy czasu, wiec przyjmujemy, że jest to wartość rzeczywista, czyli jej błąd przyjmujemy ΔCtx=0
Δlx - błąd odczytu długości odcinka na ekranie oscyloskopu, przyjmujemy go jako najmniejszą możliwą do odczytu jednostkę na podziałce oscyloskopu Δlx=0,2
- pomiar metodą porównawczą - krzywe Lissajous
Układy do pomiaru częstotliwości za pomocą oscyloskopu metodą porównawczą (krzywych Lissajous)
W metodzie tej częstotliwość fx wyznaczana jest z zależności: ![]()
gdzie: f y - częstotliwość sygnału z wzorcowego generatora, dołączonego do wejścia Y oscyloskopu,
Nx , Ny -liczby przecięć figury Lissajous na ekranie oscyloskopu z liniami: poziomą (x) i pionową (y), nie przechodzącymi przez węzły uzyskanej figury
|
Nx |
Ny |
fw [Hz] |
f [Hz] |
Δf [Hz] |
δf [%] |
f1 |
1 |
1 |
8100 |
8 100 |
860 |
10,62 |
f2 |
1 |
1 |
3050 |
3 050 |
7 |
0,23 |
f3 |
6 |
2 |
4450 |
1 483 |
7 |
0,45 |
|
1 |
1 |
1510 |
1 510 |
20 |
1,32 |
f4 |
6 |
2 |
2200 |
733 |
1 |
0,18 |
|
1 |
1 |
740 |
740 |
8 |
1,08 |
Zauważamy, iż różnice wynikające z doboru krzywych Lissajous są nie wielkie. Co oznacza, że wpływ oscyloskopu na niedokładność pomiaru jest znikomy. Błąd metody wynikać z braku możliwości ustawienia nieruchomej figury Lissajousa, co spowodowane jest rozdzielczością generatora wzorcowego (małe przesunięcie pokrętła na generatorze powoduje widoczną zmianę prędkości i kształtu figury)
Błąd ten można oszacować przyjmując jako wartość poprawną częstotliwości tą zmierzoną częstościomierzem. Błąd bezwzględny: ![]()
Błąd względny: 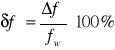
Pomiar częstotliwości przebiegów okresowych za pomocą częstościomierza cyfrowego
- pomiar częstotliwości z automatycznym i ręcznym wyborem zakresu
Pomiary wykonaliśmy są za pomocą częstotliwościomierza cyfrowego typu PFL30 o zakresie częstotliwości mierzonej: 1 Hz-50 MHz; napięciu wejściowe sinusoidalnym: min 50 mV, max 50 V oraz poziomie wyzwalania automatycznym.
Pomiary: |
|
|
f [Hz] |
f1 |
8960 |
f2 |
3057 |
f3 |
1490 |
f4 |
732 |
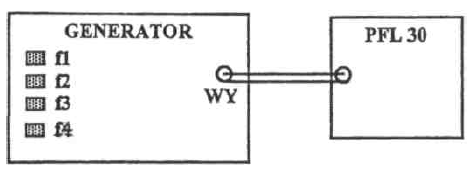
Schemat układu do pomiaru częstotliwości
za pomocą częstościomierza PFL30
fx [Hz] |
Metoda bezpośrednia |
Metoda porównawcza |
|
|
Częstościomierz PFL30 |
Oscyloskop |
|
f1 [Hz] |
8960 |
8 771,93 |
8 100 |
Δ f1 [Hz] |
- |
307,79 |
860 |
f2 [Hz] |
3057 |
2 941,18 |
1 483 |
Δ f2 [Hz] |
- |
86,51 |
7 |
f3 [Hz] |
1490 |
1 449,28 |
1 510 |
Δ f3 [Hz] |
- |
42,01 |
7 |
f4 [Hz] |
732 |
704,23 |
740 |
Δ f4 [Hz] |
- |
19,84 |
20 |
Wnioski z pomiarów częstotliwości:
Wyniki pomiarów metodą bezpośrednią i metodą krzywych Lissajous dały podobne wyniki, jednak pomiar bezpośredni jest bardziej dokładniejszy. Na błędy metody bezpośredniej wpływa przede wszystkim błąd generatora podstawy czasu, a na pomiar metodą Lissajous - błędy generatora częstotliwości wzorcowej oraz trudnością uzyskania idealnie nieruchomego obrazu (im większa częstotliwość badana tym bardziej jest to trudne).
Pomiar przesunięcia fazowego za pomocą oscyloskopu
-metoda bezpośrednia
Układ pomiarowy
Pomiary |
Obliczenia |
|||
f [Hz] |
Ctx [mS] |
lφ |
Δt |
φ |
100 |
1 |
0,6 |
0,6 |
21,6 |
150 |
1 |
0,6 |
0,6 |
32,4 |
200 |
0,5 |
1 |
0,5 |
36,0 |
250 |
0,5 |
1 |
0,5 |
45,0 |
300 |
0,5 |
0,9 |
0,45 |
48,6 |
350 |
0,5 |
0,8 |
0,4 |
50,4 |
400 |
0,2 |
2 |
0,4 |
57,6 |
450 |
0,2 |
1,9 |
0,38 |
61,6 |
500 |
0,2 |
1,8 |
0,36 |
64,8 |
550 |
0,2 |
1,7 |
0,34 |
67,3 |
600 |
0,2 |
1,6 |
0,32 |
69,1 |
650 |
0,2 |
1,5 |
0,3 |
70,2 |
700 |
0,2 |
1,4 |
0,28 |
70,6 |
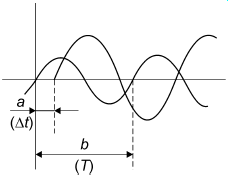
Obserwując na ekranie oscyloskopu sygnały wejściowy i wyjściowy filtru można wyznaczyć przesunięcie fazowe między nimi z zależności: ![]()
Na błąd metody składa się głównie błąd odczytu długości. Błąd ten można było zredukować stosując kursory jednak zespół popełnił błąd grupy przy pomiarach
-metoda elipsy
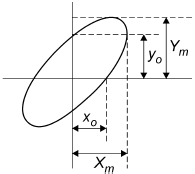
Pomiar przesunięcia fazowego sygnału metodą elipsy również wykorzystuje zjawisko powstawania krzywych Lissajous. Na jedno z wejść oscyloskopu podawany jest sygnał o danej częstotliwości, a na drugie - ten sam sygnał o tej samej częstotliwości, lecz przesunięty w fazie (za przesunięcie odpowiada włączony w tor sygnału czwórnik liniowy powodujący opóźnienia zależne od częstotliwości). Ponieważ na wejściach jest ta sama częstotliwość powstaje elipsa (krzywa Lissajous dla![]()
), która jest całkowicie nieruchoma. W zależności od przesunięcia fazowego podawanych sygnałów elipsa ta może być obrócona. Na podstawie jej wymiarów można wyznaczyć przesunięcie fazowe między sygnałami z zależności: ![]()
f [Hz] |
x0 |
xM |
y0 |
yM |
φx |
φy |
101 |
1,8 |
4,4 |
0,6 |
2 |
24,1 |
17,5 |
147 |
2,3 |
4,3 |
0,8 |
1,7 |
32,3 |
28,1 |
196 |
2,8 |
4,1 |
0,8 |
1,5 |
43,1 |
32,2 |
252 |
3,1 |
4 |
0,9 |
1,4 |
50,8 |
40,0 |
301 |
3,3 |
3,9 |
0,9 |
1,1 |
57,8 |
54,9 |
349 |
3,4 |
3,8 |
0,8 |
1 |
63,5 |
53,1 |
397 |
3,5 |
3,8 |
0,8 |
1 |
67,1 |
53,1 |
448 |
3,6 |
3,7 |
0,75 |
0,8 |
76,6 |
69,6 |
Wyznaczenie przesunięcia fazowego metoda elipsy jest obarczone znacznym błędem (3%±10%). Błąd ten zależy głównie od niedokładności pomiaru odpowiednich odcinków na ekranie oraz różnicy przesunięć fazowych wprowadzanych przez tor X i Y, stanowiącej błąd fazowy oscyloskopu.
Charakterystyki fazowo-częstotliwościowa czwórnika liniowego, który jest filtrem dolnoprzepustowy II-go rzędu
Wnioski z pomiarów przesunięcia fazowego:
Dokładniejszą metodą wyznaczenia przesunięcia fazowego z zastosowanych przez nasz zespół okazała się metoda bezpośrednia. Powodem mniejszej dokładności pomiarów metodą elipsy jest błąd fazowy oscyloskopu. Błąd ten można określić podając na oba wejścia Y i X ten sam sygnał sinusoidalny. Jeśli błąd by nie występował otrzymalibyśmy odcinek linii prostej.
Wnioski ogólne:
Na każdy z pomiar oscyloskopem mają wpływ: niedokładna kalibracja generatora podstawy czasu i wzmacniacza w torze X (rzędu 2% - 3%), niedokładności wzmacniaczy i dzielników napięciowych toru sygnału badanego, negatywny wpływ impedancji przewodów doprowadzających na kształt sygnału. Niektóre z tych niepewności można zmniejszyć stosując kompensację za pomocą sondy i kalibrację podstawy czasu wzorcową częstotliwością. Oprócz tego na pomiar mają wpływ niedokładność wykonania podziałki na ekranie oscyloskopu.
Mimo tych błędów oscyloskop okazał się w miarę dokładnym przyrządem pomiarowym. Jego największym plusem okazała się jego uniwersalność. Dzięki niemu mogliśmy zmierzyć: napięcie, okres i częstotliwość sygnału oraz jego przesunięcie fazowe względem innego sygnału.
Wykaz aparatury
oscyloskop HUNG CHANG typu 5604;
częstościomierz cyfrowy PFL-30;
generatory: RC typ PO-20 i KZ1118;
zasilacz typu KP16102;
źródło czterech mierzonych częstotliwości;
czwórnik liniowy;
Wyszukiwarka
Podobne podstrony:
Sprawko metro, Mechatronika AGH IMIR, rok 2, sprawozdania, metrologia, METROLOGIA
EAP Sprawozdanie Lab7, AGH, Semestr IV, Podstawy automatyki[Ornacki,Pakuła,Łukomski,Snamina], EAP Sp
Metro-jakas sciaga, AGH, Semestr IV, Metrologia[Nieciąg], Ściągi, Ściągi
sprawko10, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMiR, Au
sprawko6, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMiR, Aut
sprawko z pneumatyki, AGH, semestr 5, Metrologia (Jastrzębski), z chomika, pneumatyka sprawko, z dc,
PKM-wały, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMiR, Aut
sprawko M4, AGH Imir materiały mix, Studia
sprawko M4 (1), AGH Imir materiały mix, Studia
Sprawko z wymywalnosci, agh, ochrona środowiska
Sprawko poprawione, AGH, semestr 5, MIUT, miut, liny tarcie
Metro pyt. I kolos, ZiIP, ZiIP, R2, SI, Metrologia
sprawko 5, Politechnika Wrocławska, W-5 Wydział Elektryczny, Fizyka G2, fiza laborki, fiza kalit, fi
tabelka air mt, Akademia Górniczo-Hutnicza AGH, Wydział Inżynierii Mechanicznej i Robotyki WIMiR IMi
sprawko temat2, AGH, Nowoczesne technologie badania deformacji, Temat2
Ćwiczenie M 5 - Oscyloskop - Sprawozdanie, Energetyka AGH, semestr 4, IV Semestr, Metrologia, LABO
Tmm sprawko 1, Mechatronika AGH IMIR, rok 2, TMM
więcej podobnych podstron