Laboratorium Elektrotechniki
Nazwisko i Imię: Romanowski Daniel					Grupa: ED 3.5
Data wykonania: 1998.11.26		Ćwiczenie nr: 8	Temat: Stany nieustalone w obwodach RC.
ZALICZENIE		Ocena	Data		Podpis

Skład grupy:

Firlej Tomasz

Gontarz Grzegorz

Romanowski Daniel

Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z warunkami panującymi podczas ładowania i rozładowywania kondensatora i praktyczne sprawdzenie stanu nieustalonego w obwodzie RC.

Układ pomiarowy zestawiliśmy na podstawie poniższego schematu:

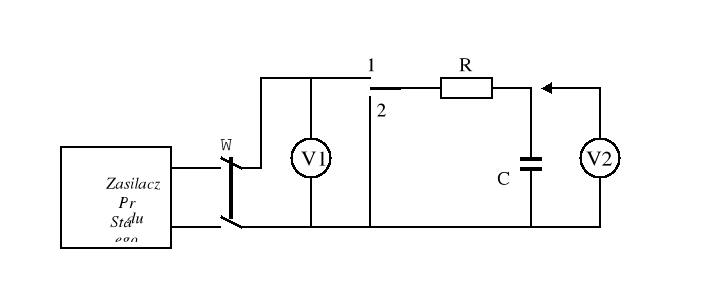
Oznaczenia elementów:

1. woltomierz magnetoelektryczny;

2. woltomierz lampowy;

18. rezystor;

C- kondensator.

1. Ładowanie kondensatora:

Lp.	C1=18μF R1=4MΩ τ1 = 72s					C2=10μF R2=1MΩ τ2 = 10s				C3=10μF R3=4M τ3 = 40s
		t	u	uc	uR	i	u	uc	uR	i	u	uc	uR	i
		[s]	[V]	[V]	[V]	[μA]	[V]	[V]	[V]	[μA]	[V]	[V]	[V]	[μA]
1	0	1,25	0	1,25	0,313	0,95	0	0,95	0,950	1,25	0	1,25	0,313
2	30			0,39	0,86		0,215		0,82		0,13	0,130		0,57	0,68	0,170
3	60			0,61	0,64		0,160		0,90		0,05	0,050		0,88	0,37	0,093
4	90			0,77	0,48		0,120		0,91		0,04	0,040		1,03	0,22	0,055
5	120			0,87	0,38		0,095		0,92		0,03	0,030		1,10	0,15	0,038
6	150			0,95	0,30		0,075		0,92		0,03	0,030		1,14	0,11	0,028
7	180			1,00	0,25		0,063							1,16	0,09	0,023
8	210			1,04	0,21		0,053							1,18	0,07	0,018
9	240			1,07	0,18		0,045							1,18	0,07	0,018
10	270			1,10	0,15		0,038							1,19	0,06	0,015
11	300			1,11	0,14		0,035
12	330			1,12	0,13		0,033
13	360			1,13	0,12		0,030
14	390			1,13	0,12		0,030

Przykładowe obliczenia:

τ₁ = R₁C₁ = 18μF ^. 4MΩ = 72s

τ₂ = R₂C₂ = 10μF ^. 1MΩ = 10s

τ₃ = R₃C₃ = 10μF ^. 4MΩ = 10s

Charakterystyki zależności u_C = f(t), u_R = f(t), i = f(t) ładowania kondensatora dołączyłem wykonane na papierze milimetrowym.

2. Rozładowanie kondensatora

Lp.	C1=10μF R1=4MΩ τ1 = 40s			C2=18μF R2=4MΩ τ2 = 72s
		t	uc	i	t	uc	i
		[s]	[V]	[μA]	[s]	[V]	[μA]
1	0	0,17	-0,043	0	1,20	-0,300
2	40	0,50	-0,125	72	0,51	-0,128
3	80	0,22	-0,055	144	0,23	-0,058
4	120	0,10	-0,025	216	0,12	-0,030
5	160	0,05	-0,013	288	0,07	-0,018
6	200	0,03	-0,008	360	0,03	-0,008

Charakterystyki zależności u_C = f(t), i = f(t) rozładowania kondensatora dołączyłem wykonane na papierze milimetrowym.

Wnioski:

Otrzymane wyniki mogą być obarczone błędem wynikającym z faktu, iż przy obliczeniach nie uwzględniłem rezystancji wewnętrznej użytych woltomierzy.

Stałe czasowe τ były wyznaczane jako czas, po którym napięcie na kondensatorze (podczas ładowania) osiągnęło 63,2% napięcia na kondensatorze w stanie ustalonym, oraz przy badaniu rozładowania kondensatora jako 36,8% napięcia na kondensatorze w chwili t = 0s. Jak widać stałe te mają wartości zbliżone do wartości teoretycznych obliczonych z wartości użytych elementów (R i C).

Czas ładowania jak i rozładowania zgodnie z teorią rośnie wraz ze wzrostem stałej czasowej τ .

---