Wydział Inżynierii Środowiska	Dzień/godz. Środa 11.15 - 14.00			Nr zespołu
		Data 14.03.2007			1
Nazwisko i Imię	Ocena z przygotowania		Ocena z sprawozdania		Ocena
1. Cichecka Agnieszka	5		5-
2. Miecznikowski Kamil	5		5-
3. Mróz Marta	5		5-
Prowadzący:		Podpis
dr Urszula Laudyn		prowadzącego

SPRAWOZDANIE

TEMAT: Wyznaczanie współczynnika lepkości.

1. Cel ćwiczenia

Celem doświadczenia jest wyznaczenie lepkości oleju i gliceryny poprzez wyznaczenie wartości pośredniej a mianowicie prędkości granicznej wrzucanych do powyższych cieczy kulek.

2. Podstawy teoretyczne

Lepkość cieczy jest miarą jej tarcia wewnętrznego, które jest spowodowane przekazywaniem pędu przez warstwy płynu poruszające się szybciej warstwom wolniejszym. Dla opisania zjawiska najlepiej posłużyć się prostym doświadczeniem.

Płaską deseczkę leżąca na powierzchni cieczy w szerokim, płytkim naczyniu, ciągniemy siłą F, nadając jej stałą prędkość V₀. Warstwa cieczy przylegająca do deseczki ma prędkość taką samą jak deseczka a kolejne, leżące coraz głębiej warstwy, mają prędkości coraz mniejsze. Warstwa cieczy przylegająca do dna jest nieruchoma. Zatem im płytsze naczynie, tym szybciej maleje wraz z głębokością prędkość cieczy.

Z doświadczenia wynika, że wielkość tych zmian powiązana jest z działającą siłą zależnością:

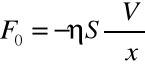
η - współczynnik lepkości charakteryzujący płyn [jednostka:

S - powierzchnia deski

- gradient prędkości przesuwanych warstw cieczy

Istnieje wzór na wyznaczenie tzw. stałej Raynoldsa charakteryzującej przepływ.

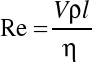
V - prędkość ciała

ρ - gęstość ciała

l - wymiar liniowy

η - współczynnik lepkości charakteryzujący płyn

Re << 1 - przepływ jest laminarny - bezwirowy

Re > 1 - przepływ jest turbulentny

Przepływu laminarnego dotyczy prawo o podobieństwie przepływów:

Przepływy dwóch cieczy o różnych lepkościach są podobne, jeżeli odpowiada im taka sama liczba Raynoldsa.

Na ciało spadające w pojemniku z cieczą działają trzy siły:

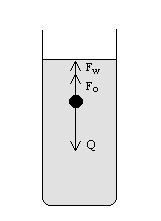
Q - siła grawitacji

F_w - siła wyporu

F_a - siła lepkości

Siła wypadkowa w trakcie opadania kulki w pewnym momencie stabilizuje
się i zachodzi wyrównanie się sił F_w + F_o = Q , a siła wypadkowa wynosi zero.

Graficzne przedstawienie prędkości:

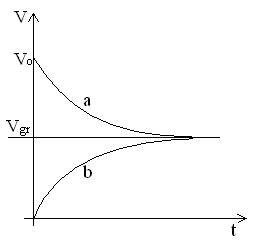
Linie a i b są zależne od V_o.

a - V_o > V_gr

b - V_o = 0

3. Przebieg doświadczenia

Na początku dokonaliśmy pomiarów mas i średnic kulek. Dysponowaliśmy 5 kulkami małymi, 5 średnimi i 3 dużymi. W celu zmniejszenia błędu zważyliśmy kulki danego wymiaru razem (Jako, że kulki ważyliśmy na bibułce, musieliśmy odjąć jej masę od wyniku.) i przyjęliśmy średnią jako masę jednej kulki. Następnie wykorzystując jedną kulkę dużą i jedną małą określiliśmy dla każdego z cylindrów drogę, na której ruch kulek uznaliśmy za jednostajny. Dla ustalonych dróg zmierzyliśmy czas opadania każdej z kulek. Wyniki pomiarów przedstawiają poniższe tabele.

Kulki małe Kulki średnie

średnica [mm]		czas [s]			średnica [mm]		czas [s]
							olej	gliceryna				olej	gliceryna
2,53			8,16		56,00			2,99		6,09	20,84
2,54			8,15		52,25			3,00		6,02	21,50
2,54			8,22		52,62			2,99		6,07	20,40
2,53			8,22		57,62			2,99		5,94	21,12
2,54			8,19		51,97			2,99		5,94	22,16

Kulki duże

średnica [mm]		czas [s]
				olej	gliceryna
3,10			4,82	16,25
3,05			4,65	15,78
3,05			4,56	16,22

W przypadku jednej z kulek średnich otrzymaliśmy czas opadania w glicerynie wynoszący 37,63s. Pominęliśmy ten pomiar w dalszych obliczeniach jako obarczony błędem grubym.

Dane potrzebne do obliczeń:

gęstość cieczy [g/cm^3]	gliceryna	1,473
		olej	0,867
	średnica wewnętrzna rury [mm]	gliceryna	(28,0±0,1)
		olej	(27,2±0,1)
	długość słupa cieczy [cm]	gliceryna	(84,0±0,1)
		olej	(75,0±0,1)
przyspieszenie ziemskie [m/s^2]		9,81

4. Wyniki i obliczenia

Błędy pomiaru masy i średnicy:

• Kulka mała:

∆m= 0,01 mg

d_śr = 2,54 mm

∆d = 0,005 mm

r = 1,27 mm

∆r = 0,003mm

• Kulka średnia:

∆m = 0,01 mg

d_śr = 2,99 mm

∆d = 0,004 mm

r = 1,50 mm

∆r = 0,002 mm

• Kulka duża:

∆m= 0,01 mg

d_śr = 3,07 mm

∆d = 0,029 mm

r = 1,53 mm

∆r = 0,014 mm

Błędy pomiaru średnic są obliczone na podstawie odchylenia standardowego. Obliczenie w ten sposób błędu pomiaru masy nie było możliwe, ponieważ nie ważyliśmy każdej kulki oddzielnie. W związku z tym jako błąd pomiaru masy przyjęliśmy błąd systematyczny.

Błędy pomiaru czasu:

błąd systematyczny stopera = 0,01s

błąd refleksu = 0,2s

∆t = (0,01+0,2)s = 0,21s

Błąd pomiaru drogi:

∆S=0,1cm

Wyniki obliczeń prędkości:

Błąd wyznaczenia prędkości wyznaczamy za pomocą odchylenia standardowego.

• Kulki małe:

olej
S[cm]		t[s]		V[cm/s]
75,0±0,1		8,16±0,21		9,191176±0,248793
75,0±0,1		8,15±0,21		9,202454±0,249388
75,0±0,1		8,22±0,21		9,124088±0,245263
75,0±0,1		8,22±0,21		9,124088±0,245263
75,0±0,1		8,19±0,21		9,157509±0,247018
gliceryna
S[cm]		t[s]		V[cm/s]
84,0±0,1		56,00±0,21		1,500000±0,007411
84,0±0,1		52,25±0,21		1,607656±0,008375
84,0±0,1		52,62±0,21		1,596351±0,008271
84,0±0,1		57,62±0,21		1,457827±0,007049
84,0±0,1		51,97±0,21		1,616317±0,008455


V_śr=9,159863 V_śr=1,55563

∆V_śr=0,036605 ∆V_śr=0,071951

• Kulki średnie:

olej
S[cm]		t[s]		V[cm/s]
75,0±0,1		6,09±0,21		12,31527±0,441085
75,0±0,1		6,02±0,21		12,45847±0,4451209
75,0±0,1		6,07±0,21		12,35585±0,443942
75,0±0,1		5,94±0,21		12,62626±0,463218
75,0±0,1		5,94±0,21		12,62626±0,463218
gliceryna
S[cm]		t[s]		V[cm/s]
84,0±0,1		20,840±0,21		4,030710±0,045415
84,0±0,1		21,500±0,21		3,906977±0,042812
84,0±0,1		20,400±0,21		4,117647±0,047290
84,0±0,1		21,120±0,21		3,977273±0,044282
84,0±0,1		22,160±0,21		3,790614±0,040435


V_śr=12,47642 V_śr=3,964644

∆V_śr=0,146402 ∆V_śr=0,124043

• Kulki duże:

olej
S[cm]		t[s]		V[cm/s]
75,0±0,1		4,82±0,21		15,56017±0,698679
75,0±0,1		4,65±0,21		16,12903±0,749913
75,0±0,1		4,56±0,21		16,44737±0,779374
gliceryna
S[cm]		t[s]		V[cm/s]
84,0±0,1		16,25±0,21		5,169231±0,072956
84,0±0,1		15,78±0,21		5,323194±0,077178
84,0±0,1		16,22±0,21		5,178792±0,073215




V_śr=16,04552 V_śr=5,223739

∆V_śr=0,449458 ∆V_śr=0,086263

Obliczenie lepkości:

Lepkość obliczamy dla każdej wielkości kulki ze wzoru:


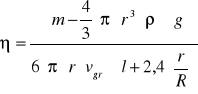
m- masa kulki

r - promień kulki

ρ - gęstość cieczy

g - przyspieszenie ziemskie

R - promień cylindra

l - długość słupa cieczy

Następnie obliczamy średni wynik dla każdej cieczy. Błędy obliczamy za pomocą różniczki zupełnej:




Olej
Współczynnik lepkości [ ]	0,0000381±0,0000043
Gliceryna
Współczynnik lepkości [ ]	0,0149561±0,0005693

5. Wnioski

Celem naszego ćwiczenia było wyznaczenie współczynnika lepkości oleju i gliceryny. Zauważyliśmy, że w trakcie obliczeń dużą rolę odgrywają błędy. Przy wyznaczaniu czasu musieliśmy uwzględnić także refleks osoby mierzącej.

W przypadku naszego ćwiczenia V₀>V_gr, więc kulka z biegiem czasu zmniejszała swoją prędkość aż osiągnęła V_gr. Następowało to w górnej części cylindra.

Udało nam się wyznaczyć prędkości graniczne V_{gr oleju} i V_{gr gliceryny} oraz współczynniki lepkości
_oleju i
_gliceryny.

1
















---