F I Z Y K A 2

1. Pole elektryczne. Prawo Coulomba. Natężenie pola elektrostatycznego E.

q⁽⁺⁾ q^(-) e - ład. elementarny

1C = 1A ⋅ 1s

e ≅ 1,602 ⋅ 10^-19 C

Prawo Coulomb-a

r(w.)

a₁ a₂

ε₀ ≅ 8,85 ⋅ 10^-12 F/m - przenikalność elektryczna próżni

zasada superpozycji

Natężenie pola elektrycznego

Niech Q - wytwarza pole

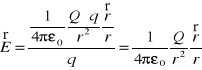
Q₊ - linie na zewn. Q_- - linie do wewn.

- zasada superpozycji

Ładunek rozciągły

1. Ładunek liniowy λ - gęstość liniowa ładunku

λ [λ] = [C/m]

2. Ładunek powierzchniowy σ - gęstość powierzchniowa ładunku [σ] = [C/m²]

3. Ładunek objętościowy (przestrzenny).

ρ - gęstość objętościowa ładunku

[ρ] = [C/m³] ρ = dQ/dV

gdy E(w.) ⊥ S => Φ_E = E ⋅ S

2. Strumień wektora natężenia pola elektrostatycznego. Prawo Gaussa.

Tw. Gauss-a

Całkowity strumień nat. pola E(w.) przez pow. zamkniętą S = całkowity ład. zawarty wewnątrz pow. S / ε₀

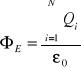
E(w.) ⊥ S

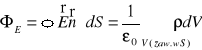
Równanie całkowe - prawo Gaussa

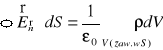
3. Praca sił pola elektrostatycznego.

Energia potencjalna elektrostatyczna.

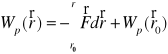
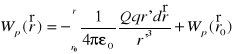
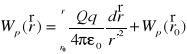
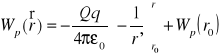
r₀ -> ∞ W_p(∞) = 0

Praca na przeniesienie ład. z r₀ do r

W = W_p(r) - W_p(r₀)

4. Potencjał elektrostatyczny. Związek między potencjałem i natężeniem pola.

Potencjał elektryczny.

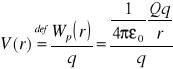
- skalar V(∞) = 0

W_p(r) = q ⋅ V(r)

W = W_p(r) - W_p(r₀) = q V(r) - q V(r₀)

W = q [ V(r) - V(r₀) ] = q ⋅ ΔV

Ogólnie

=>

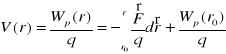
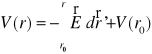
Poten-cjał el. od ładunku rozcią-głego

Różnicowy związek między nat. pola E(w.) a potencjałem V.

(1) dr'(w.)

r₀(w.)

(2)

r(w.)

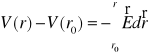
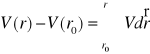
E(w.) = -∇V

W układzie kartezjańskim:

E(w.) = -∇V = [-∂V/∂x , -∂V/∂y , -∂V/∂z ] =

= - [ ∂V/∂x , ∂V/∂y , ∂V/∂z ] ∇ϕ

E_X E_Y E_Z

5. Dipol elektryczny. Moment dipolowy. Potencjał i natężenie pola od dipola.

Dipol elektryczny.

p (w.) moment dipolowy

p(w.) =(df) q l(w.)

+q l -> 0 |

q -> ∞ | => p(w.) = const

l (w.)

-q

Potencjał i natężenie pola elektr. E(w.) od dipola elektr.

p(w.)

α r₁ (w.) P

+q r (w.)

α

l 90⁰

r₂ (w.)

-q

1. Obliczamy V(P)

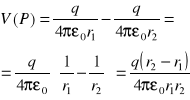
r² - r₁ = l cosα α = ∠( p(w.) , r(w.) )

r₁ r₂ ≅ r²

V ∼ 1/r² Dla ład. punktowego V ∼ 1/r

Dla dipola V ∼ 1/r²

q l=|p(w.)|

2. Obliczamy nat. pola E(w.) (od dipola)

E_r

p (w) P

r (w.)

+q ∂s E

dα E_α

-q

E(w.) = -gradV = -∇ V

E(w.) = [E_r , E_α ] ; E_r = -∂V/∂r ; E_α = -∂V/∂s,

∂s = r ∂α ; E_α = - ∂V / r∂α

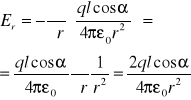
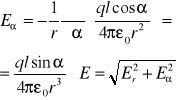
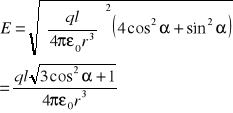
Dla ładunku punktowego E ∼ 1/r²

Dla dipola E ∼ 1/r³

Gdy α=0 E_r=2ql / 4πε₀r³ , E_α=0

α=π/2 E_r=0 E_α=ql / 4πε₀r³

6. Dipol w zewnętrznym polu elektrycznym. Moment siły i energia dipola.

Dipol elektryczny w zewnętrznym polu E(w.)

1. Energia dipola p(w.) w polu E(w.)

-q r₂(w.) +q

R(w.)+r₁(w.) R

R(w.)+r₂(w.)

R(w.), r₂(w.), r₁(w.)

W_d = qV(R+r₂)-qV(R+r₁)=q[V(R+r₂)-V(R+r₁)]

W_d = q|r₂-r₁| ⋅ ΔV/|r₂-r₁|= -q|r₂-r₁| ⋅ (- ΔV/|r₂-r₁|)

p

W_d = - p(w.) E(w.) E_p -s. pola (na kier. P(w.)

a) ↑E(w.) ↑p(w.) W_d = -E⋅ p < 0

b) ↑E(w.) →p(w.) W_d = 0 α = π/2

c) ↑E(w.) ↓p(w.) W_d = p E > 0

2. Obliczam moment siły działającej na dipol przez pole elektr. (E(w.) )

y

r

F₁(w.) P(w.)

x

M (w.) = r(w.) x F(w.) M = ∂W / ∂α

α=∠( p(w.) , E(w.) ) M= ∂/∂α (-p ⋅ E cosα)

= p E sinα M(w.) = p(w.) x E(w.)

Liczenie dokładne dla dowolnego pola E(w.)

M(w.) = p(w.) x E(w.) + R(w.) x (p(w.) ⋅ V(w.))

V=[∂/∂x ; ∂/∂y ; ∂/∂z]

7. Metale w polu elektrycznym.

Metale (przewodniki)

1. Bardzo duża liczba ład. swobodnych.

- +

E_z - + V = const.

- + dla metali

E = - ∇V = 0

2. Natężenie pola E(w.) przy powierzchni metalu. E = σ/ε₀

E(w.) ⊥ do pow. metalu

σ - gęst. pow. ład w

metal metalach

E = 0 Obliczam E przy pow.

met.

σ z tw. Gaussa

Φ_E = SE = Sσ / ε₀

3. Fale elektryczne we wnęce metalu.

( Γ - kontur zamknięty ) Niech na pow. wewn. będzie ładunek.

S - zamknięta powierzchnia Gaussa

Φ_E = 0 = Q_C / ε₀

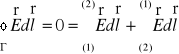
Wniosek: E(w.) - we wnęce = 0 => Q we wnęce = 0

4. Gromadzenie się ładunku na ostrzach metalu.

σ_R σ_r

≡ R r

Szuk. powiązania między „σ_R” „σ_r” „a” „R” i „r”

Całkowite ładunki na kulach wynoszą:

Q_R = σ_R 4πR² Q_r = σ_r 4πr²

Potencjały kul wynoszą:

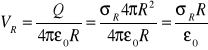
Ale V_R = V_r

8. Kondensatory. Pojemność elektryczna kondensatora. Energia kondensatora.

Pojemność elektryczna. Kondensatory.

Pojemność elektryczna.

metal

+Q -Q

ΔU = U

Q wywołuje powstanie różnicy potencjałów ΔV

ΔU = U - napięcie U ∼ Q => U = 1/C Q

1/C - wsp. poj.

C - pojemność elektryczna układu 2-óch elektrod C =(df) Q / U

Kondensator - układ dwóch elektrod metalowych

1. Kondensator płaski. (d - odl. okł. S - pow. okładki) C=Q/U ; E=σ/ε₀ ; σ=Q/S ;

C = σ⋅S / E⋅d = σS / (σ/ε₀ ⋅ d) = ε₀S / d

Napięcie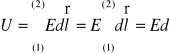

2. Kondensator walcowy.

a - promień wewn.

b - pr. zewn.

l - wys.

3. Kondensator kulisty. (r - wewn, R- zewn.)

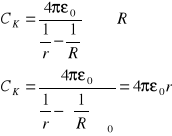
Energia kondensatora (elektrycz.)

(przeniesienie ład. z okładki na drugą)

U' = Q' / C , dW_C = U' dQ'

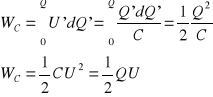
Jednostki pojemności

Jednostka C [C] = [F] (farad) 1F=1C/1V =

= 1A⋅1s / 1V

9. Energia pola elektrycznego.

Energia układu N ładunków punktowych.

a) gdy N=2

q₂

r₁₂

q₁

W_C = W₁₂ = q₁q₂/4πε₀r₁₂

b) N=3

W_C = W₁₂ + W₁₂₃ = q₁q₂/4πε₀r₁₂ + q(V₁ + V₂)

W_C = q₁q₂/4πε₀r₁₂ + q₁q₂/4πε₀r₁₃ + q₁q₂/4πε₀r₂₃

c) N - ładunków W_C = ½ (1 / 4πε₀ ∑a_iq_i/r_ij)

Energia potencjalna jednorodnie naładowanej kuli ładunku Q i promieniu R.

dW_p = Q_rdQ / 4πε₀r ; Q_r = 4/3 πr³ρ

ρ = Q / (4/3 πR³) ; dQ = 4πr²ρdr

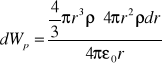
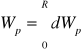
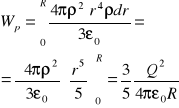
Energia pole el. w próżni i dielektryku.

1.

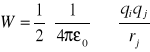
2.

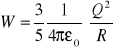
3.

4.

5.

10. Pole elektryczne w dielektrykach.

metal+ + + + + + + + σ_sw

- - - - - - ↑↓P σ_pol

↓ E=E₀-E_pol

- - - - - - - - σ_pol

+ + + + + + + + σ_sw

Szukamy natęż. pola el. E w dielektryku korzystając z tw. Gaussa

E₀ = σ_sw / ε₀ Φ_E = SE = (Sσ_sw - Sσ_pol) / ε₀

E = σ_sw / ε₀ - σ_pol / ε₀ => E = σ_sw / ε₀ - P / ε₀

P ∼ E

E= σ_sw / ε₀ - (ε₀ χ E / ε₀) χ - podatn. el. diel.

E = E₀ - χ E => E + χ E = E₀ => E(1+χ) = E₀

ε = 1 + χ - wzgl. przenik. el. dielektryka

E = E₀ / ε

11. Wektor polaryzacji P. Polaryzowalność.

Chociaż w dielektrykach ładunki nie mogą się poruszać po przyłożeniu pola elektrycznego, to jednak ich położenie ulega wówczas niewielkiemu przemieszczeniu, zgodnemu z kierunkiem przyłożonego pola.

To przemieszczenie to polaryzacja dielektryka.

↑P S

+ + + + + + + Q σ_pol

E(w.)↑ - - - - - - -

↑P σ_pol

Średni moment dipolowy w jednostce objętości.

P(w.) =(df.) 1/V ∑ P_i(w.) P = np = nqυ

n - ko... elem. dipoli

σ_pol = Q_pol / S = Sυnq / S = nqυ = P

σ_pol = P(w.) n(w.)

n(w.) || P(w.) to σ_pol = P

n(w.) ⊥ P(w.) to σ_pol = 0

12. Podatność dielektryczna χ i względna przenikalność elektryczna ε.

Polaryzacja dielektryka powoduje powstanie pola przeciwnie skierowanego w stosunku do pola zewnętrznego. Wartość tego pola jest dla większości materiałów proporcjonalna do istniejącego pola w dielektryku:

E(w.) = E_o(w.) - χ E(w.)

Gdzie E - natężenie pola w dielektryku, E₀ - nat. pola w nieobecn. diel. ,

χ jest współczynnikiem proporcjonalności, zwanym podatnością elektryczną dielektryka.

=> E + χE = E₀ => E ( 1+χ ) = E₀

Pole w dielektryku ulega osłabieniu 1+χ = ε razy. Czynnik ten nosi nazwę względnej stałej dielektrycznej (przenikalności elektrycznej).

13. Związek pomiędzy natężeniem pola, wektorem polaryzacji i wektorem indukcji.

Trzy wektory elektryczne:

D(w.) - w. indukcji elektryczn. (przesunięcia)

E(w.) - w. natężenia pola el.

P(w.) - w. polaryzacji

W dielektrykach wektory E(w.) , P(w.), D(w.) są współliniowe

P = ε₀ (ε - 1) E D = ε₀ ε E

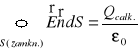
14. Pole elektryczne we wnękach dielektryka. Wzór Claussiusa - Massottiego.

1. Wnęka podłużna.

E↑

↑E₀

E₀ = E

2. Wnęka poprzeczna

E↑ σ_pol

P↑

σ_B z tw. Gaussa otrzym.:

E₀S - ES = σ_polS / ε₀ E₀ = E + σ_pol / ε₀

σ_pol = P E₀ = E + P/ε₀

3. Wnęka kulista

= +

↑E₀ ↑E E_KUL

↑E

↑P

E₀ = E - (- P / 3ε₀) = E + P /3ε₀

E₀ = E + P / 3ε₀

Równanie Claussiusa - Massottiego dla dielektryków niepolarnych

p = α_e ε₀ E₀ (1) P ≈ n ⋅ p = n α_e ε₀ E₀ ­ ale

(2) P = ε₀ (ε - 1) E

E₀ = E + P / 3ε₀ = F + (ε₀ (ε - 1) E) / 3ε₀ =

= E (1 + (ε - 1)/3) = E (ε + 2)/3

Porównanie wzorów (1) i (2)

ε₀ (ε - 1) E = n α_e ε₀ E (ε + 2)/3

ε - 1 = (n α_e (ε + 2)) / 3

(ε - 1) / (ε + 2) = n α_e / 3

n = ρ/m m = μ/N_A

n = ρN_A / μ

ρ - gęstość dielektryka;

równ. C -M dla diel. m - masa jądra atomu ;

niepol. μ - masa molowa ;

N_A - liczba Avogarda

Równanie C - M dla diel. polarnych

Dielekt. Polarn. Mają trwały moment dipolowy p₀ nawet bez obecn. zewnętrznego pola el. Po włączeniu zewn. pola el. E w dielektryku polarnym występują 2 procesy:

- pierwszy polegający na porządkowaniu ustawienia trwał. mom. dipolowych równolegle do pola el. , któremu to ustawianiu przeciwstawiają się drgania termiczne cząsteczek;

- drugi polegający na indukowaniu się dodatk. mom. dipolowych (jak w diel. niepolarn.) pod wpływem zewn. pola el.

15. Ferroelektryki. Prawo Curie - Weissa.

Budowa domenowa ferroelektryka (w jednej domenie identycznie ustawione momenty):

1. Trwałe momenty dipolowe p₀ - b. duże.

2. Bliskie położenie sąsiednich momentów

dipolowych.

Własności te wykazują: BaTiO₃ , NaTuO₃ , KH₂PO₄ , WO₃

W temp. T_C - temp Curie - ferroelektryk przechodzi w dielektryk

λ

λ = A / (T-T_C)

Prawo Curie - Weissa

ferro-

elektryk

T_C

16. Prąd elektryczny. Gęstość prądu. Różniczkowe prawo Ohma.

Prąd elektryczny - uporządkowany ruch elektronów swobodnych.

Prawo Ohma: I = U / R

Różniczkowe prawo Ohma:

σ = 1 / ρ

gęstość prądu: j = (S V_d 1s n e)/(S 1s) = n e V_d

17. Teoria przewodnictw metali Drudego - Lorenza,

gaz elektronowy

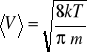
T = 300 K

<V> ≈ 1 ⋅ 10⁷ cm/s

Pojawia się prędkość dryfu (lub unoszenia) elektronu związana z działaniem pola el.

Średnia prędkość el.

V_dds

S

j = J / S ; Q = S V_d 1s n ⋅ e ;

j = S V_d ds n e / Sds = n e V_d

j = n e V_d j = σ E

Szukamy wyrażenia na przewodnictwo właściwe metalu jako funkcję parametrów opisujących elektrony swobodne w metalu.

σ = ? j = σ E j = n e V_d

porównując otrzymujemy:

σ E = n e V_d

V_d = a τ a = F_el / m = eE / m V_d = eEτ / m

τ = l / < V+ V_d> = l / ( <V> + V_d)

V_d = eEl / (m<V>)

j = n e V_d = n e² l E / (m <V>) =>

σ = n e² l / (m <V>)

j = σ E

m <V²> / 2 = E_K(w.) ≈ m <V>² / 2 = 3/2 k T

m = skT / <V>² σ = n e² l <V> / 3kT

18. Prawo Wiedemana - Franza.

λ = 1/3 n<V> lG C_V = 3k

λ = n<V> ek λ/σ = (n<V>lk3kT)/(ne²l<v>) = 3k²T/e² = L ⋅ T L - liczba Lorenza

wg metody kwant.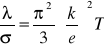

Ruchliwość elektronów

j = σE = neV_d

σ = ne V_d/E

μ = V₀/E

σ = neμ

19. Pole magnetyczne w próżni. Siła Lorenza. Wektor indukcji magnetycznej B.

(źródło pola magn. - prąd el.)

Siła Lorenza

F_L = q( V(w.) × B(w.) )

B(w.) - wektor indukcji magnetycznej

F(w.) ⊥ V(w.) , F(w.) ⊥ B

F = qVB sin (∠ V(w.),B)

gdy V(w.) ⊥ B(w.) to F = qVB

E = F / q

B = F / (qV) [B] = [T] (tesla)

Kiedy F_L = 0 V(w.) = 0 i V(w.) || B

Siła Lorenza nie może zmienić E_KIN. (nie wpływa na prędkość)

H - wektor natężenia pola magnetycznego w próżni

B = μ₀ H

μ₀ - przenikaln. magnet. próżni

μ₀ ε₀ = 1 / C² => μ₀ = 1 / (ε₀ C²)

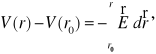
fghgf

---
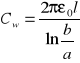
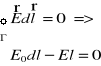