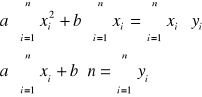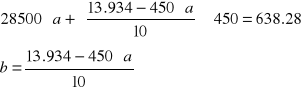|
|
Wyznaczanie współczynnika załamania światła refraktometrem Abbego.
|
|
|
|
|
|
Ćwiczenie polegało na wyznaczeniu przy użyciu refraktometru Abbego współczynników załamania światła dla wodnych roztworów gliceryny a następnie na sporządzeniu zależności tego współczynnika od stężenia danego roztworu . Przy przejściu przez granicę dwóch ośrodków światło zmienia swój kierunek ruchu . Zjawisko to, nazywane załamaniem światła zostało przedsta na rysunku1.1. 
Ilustracja 1 .Załamanie światła na granicy dwóch ośrodków
Promień biegnący ze środowiska 1 doznaje załamania na granicy AB .Kąt zawarty między promieniem padającym a prostopadłą do granicy dwóch ośrodków , nazywa się kątem padania .
Stosunek sinusa kąta padania do sinusa kąta załamania jest dla danej pary ośrodków wielkością satłą . Wartość tego stosunku nazywa się współczynnikem załamania . Współczynnik załamania można również wyrazić przez stosunek prędkości rozchodzenia się światła w tych ośrodkach :
gdzie: n - względny współczynnik załamania ośrodka 2 względem ośrodka 1
v1-v2 - prędkość światła w odpowiednich ośrodkach .
W ćwiczeniu należy wyznaczyć stężenie dwóch roztworów o znanych współczynnikach załamania światła na podstawie znanych i odczytanych wartości stężeń i współczynników załamania dziesięciu roztworów gliceryny.
Do obliczeń wykorzystam metodę najmniejszych kwadratów, co daje mi następujący układ równań :
gdzie n to liczba pomiarów = 10. Do rozwiązania tego układu wykorzystam wartości x i y
Po podstawieniu i obliczeniu sum otrzymujemy :
Z równania drugiego obliczam b i podstawiam do równania pierwszego :
Po rozwiązaniu układu równań otrzymuję ostatecznie wartość a i b :
Czyli wykresem ilustrującym wykonane ćwiczenie będzie wykres funkcji :
Tak więc wartości współczynników dla poszczególnych stężeń przyjmą wartości:
Błąd wartości stężenia roztworu wynosi:
Dla poszczególnych stężeń błędy te wynoszą:
Δc10% = 0,05 * 10% = 0,5%
Δc30% = 0,05 * 30% = 1,5%
Δc70% = 0,05 * 70% = 3,5%
Z wykresu funkcji y = 0.0014 x + 1,3304 możemy odczytać wartość stężenia roztworów nieznanych,
Δc32% = 0,05 * 20% = 1,6%
Niepewność wzorowania refraktometru wynosi ud(n) = 0,001
Niepewność eksperymentatora wynosi ue(n) = 0,003
Celem ćwiczenia było wyznaczenie współczynnika załamania światła refraktometrem Abbego. Jak pokazuje wykres zależności 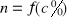
współczynnik załamania jest proporcjonalny do stężenia procentowego roztworu. Wzrost stężenia pociąga wzrost współczynnika załamania. Sporządzony wykres może stanowić podstawę do identyfikacji stężeń nieznanych roztworów. Nieznane wartości stężeń wynoszą kolejno dla x : C= 80 ± 4 % dla y : C = 32 ± 1,6 %.