Politechnika Śląska w Gliwicach Wydział Inżynierii Środowiska i Energetyki
|
SPRAWOZDANIE Z LABORATORIUM Z FIZYKI
TEMAT: Zależność lepkości wody od temperatury
Sekcja 4 Grupa3 Przemysław Górecki Czaja Mariusz |
I. Część teoretyczna.
Lepkość jest własnością gazów i cieczy. Charakteryzuje ona ich opór podczas płynięcia wywołanego siłami zewnętrznymi. Zjawisko to bywa także nazywane tarciem wewnętrznym. W ciałach stałych tarcie to jest oporem przeciwko powstawaniu odkształceń stycznych. Właściwość ta mierzona jest ilościowo współczynnikiem lepkości lub też w skrócie lepkością.
Rozpatrzmy teraz przepływ cieczy rzeczywistej przez przewód o przekroju poprzecznym r0 i długości l0. Przyjmiemy, że siła lepkości cieczy F jest proporcjonalna do gradientu prędkości dv/dr i powierzchni stykających się warstw 2πlr, czyli:
![]()
,
gdzie η - współczynnik lepkości danej cieczy. Ciecze stosujące się do tego prawa nazywamy cieczami newtonowskimi.
Współczynnik lepkości jest liczbowo równy wartości siły stycznej, która przyłożona do jednostkowej powierzchni przesuwanej warstwy utrzymuje w tej warstwie przepływ laminarny ze stałym jednostkowym gradientem prędkości warstw.
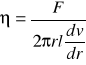
,
współczynnik ten nosi nazwę lepkości dynamicznej.
Siła F jest równoważona siłą spadku ciśnienia Δp, działającego na powierzchnię przekroju poprzecznego cylindra πr2, zatem:
![]()
,
skąd po przekształceniu i scałkowaniu w granicach od r do r0 otrzymamy związek wyrażający zależność prędkości v cieczy od promienia cylindra:
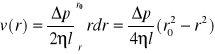
.
Jak wynika z powyższej zależności ciecz płynąca przez rurę ma paraboliczny rozkład prędkości wzdłuż promienia rury.
Oznaczmy przez Q(r) masę płynu o gęstości ρ, przepływającą w jednostce czasu przez cylinder o promieniu r. Różniczka tej wielkości wyraża się wzorem:
![]()
,
gdzie dS=2πrdr - powierzchnia pierścienia o promieniu r i szerokości dr.
Po podstawieniu otrzymamy:
![]()
,
po scałkowaniu:
![]()
.
Całkowita masa płynu przepływającego przez rurę o promieniu wewnętrznym r0 i długości l wynosi:
![]()
,
gdzie ν=η/ρ - nosi nazwę współczynnika lepkości kinematycznej.
Zależność ta nosi nazwę wzoru Poiseuille'a. Wynika z niej, że ilość wypływającej cieczy jest proporcjonalna do czwartej potęgi promienia otworu. Przytoczone tu rozważania odnoszą się do przewodów o bardzo małej średnicy, noszących nazwę kapilar.
2. Przebieg ćwiczenia.
Aparatura do wyznaczania zależności lepkości wody od temperatury znajdująca się w pracowni składa się ze zlewki, grzałki, termometru, mieszdełka, którego celem jest wyrównywanie temperatury w czasie grzania wody, kapilary, menzurki, stopera.
Ćwiczenie wykonano w sposób następujący:
1. Sprawdzono działanie urządzeń elektrycznych (grzałki i mieszadelka).
2. Sprawdzono czy ze szklanego kranu wycieka woda.
Po pozytywnym wyniku przystąpiono do dalszych czynności:
3. Odczytano temperaturę wody.
4. Pod wylot szklanego kranu podstawiono menzurkę i odkręcono kran jednocześnie włączając stoper. Zmierzono czas do jej napełnienia, a następnie wodę z menzurki wlano z powrotem do zlewki.
5. Przez uruchomienie grzałki podniesiono temperaturę wody o 10-15°C i zmierzono czas wypływu podgrzanej wody.
6. Czynność 5. powtarzano do osiągnięcia temperatury 86°C.
Tabela pomiarowa:
Temperatura
[stopnie Celsjusza] |
Czas
[s , ms ] |
Czas średni
[s , ms ] |
21 |
56,88 |
57,1 |
57,32 |
||
32 |
48,12 |
47,86 |
47,60 |
||
41 |
40,50 |
40,98 |
41,47 |
||
50 |
37,35 |
37,32 |
37,29 |
||
60 |
33,19 |
32,95 |
32,72 |
||
70 |
30,53 |
30,28 |
30,03 |
||
80 |
30,03 |
29,53 |
29,03 |
||
86 |
28,63 |
28,56 |
28,50 |
Współczynnik a z regresji logarytmicznej: a = 1131+_79 [K]
Obliczenia:
Energia aktywacji E = a × k
gdzie k - stała Bolzmana
k = 1,38044 × 10-23 [J\K]
E = a × k = 1131×1,38044 × 10-23=15,613× 10-21 [J]
Błędy:
∆E = k×∆a [J] - błąd bezwzględny
∆E =1,38044 × 10-23×79= 1,0905× 10-21 [J]
δE=∆E\E - błąd względny
δE=∆E\E = 1,0905× 10-21 [J] /15,613× 10-21 [J]= 0.07
Zestawienie wyników
E = 15,613× 10-21 +_ 0.07 [J]
5.Wnioski
Na błędy pomiarowe podczas wykonywania ćwiczenia składają się niedokładności odczytu temperatury z termometru , błąd odczytu czasu wynikający z niedoskonałości ludzkiego refleksu przy zatrzymywaniu i uruchamianiu stopera , oraz błąd wynikający z niemożliwości dokładnego odczytu poziomu cieczy w naczyniu do którego była ona przelewna przez wężyk. Na pewno wpływ na wynik miała różnica temperatur pomiędzy cieczą w wężyku i temperaturą zewnętrzną, ciecz podczas przepływu ulegała w pewnym stopniu ochłodzeniu , jednak byłoby to trudne do oszacowania i wymagało sporo czasu i podstawy z zakresu termodynamiki i mechaniki cieczy.
Obserwując przebieg wykresu zależności czasu wypływu wody od jej temperatury, zauważamy, że zależność ta, a więc również lepkość, maleje wraz ze wzrostem temperatury. Wykres potwierdza to, że zależność lepkości wody od temperatury nie jest funkcją liniową , jest natomiast funkcją ekspotencjalną.
Słuszny jest więc wzór ![]()
.
Wyszukiwarka