UKŁADY ARYTMETYCZNE, OPERACJE ARYTMETYCZNE W KODZIE ZM, ZU1, ZU2, SUMATOR

• WSTĘP

Urządzenia cyfrowe takie jak: kalkulator, maszyna cyfrowa, cyfrowy przyrząd pomiarowy itp. realizują swoje działanie na podstawie pewnych charakterystycznych (zaprogramowanych) operacji, głównie arytmetycznych i logicznych. W operacjach tych biorą udział: sumatory, komparatory, rejestry.

Sumatory dzielimy na:

• dwójkowe, gdzie działania wykonuje się na liczbach dwójkowych,

• dziesiętne, wykonujące działania na liczbach dziesiętnych kodowanych dwójkowo.

Gdy za kryterium podziału przyjmuje się sposób podawania składników sumy, wtedy można wyróżnić sumatory:

1. równoległe:

• z przeniesieniem szeregowym,

• z przeniesieniem równoległym,

1. szeregowe.

Komparatory służą do porównywania liczb binarnych w procesie wykonywania operacji arytmetycznych i logicznych, wyróżnić można dwa zasadnicze typu komparatorów:

2. komparatory iteracyjne,

3. komparatory kombinacyjne.

• PROGRAM ĆWICZENIA:

• Zmontować układ z Rys. 3-2, sprawdzić jego działanie dla operacji dodawania i odejmowania.

• Zbudować czterobitowy sumator dwójkowy dodająco-odejmujący pracujący według zadanego przez prowadzącego ćwiczenie algorytmu.

• Zbudować wielobitowy sumator dwójkowo-dziesiętny liczb BCD pracujący w zapisie "znak-uzupełnienie do 9".

• Zbudować zadany (czterobitowy) komparator równoległy i opisać jego działanie.

• Zbudować zadany (czterobitowy) komparator iteracyjny, opisać jego działanie. Porównać stopień złożoności rozwiązań obu komparatorów.

• ZAWARTOŚĆ ĆWICZENIA:

1. Sumatory jednobitowe.

Sumatory realizują sumę arytmetyczną dwu liczb binarnych. Dodanie dwu liczb dwójkowych (operandów) A i B ilustruje Tab. 3-1.




Ai	Bi	Si	Ci+1
0 0 1 1	0 1 0 1	0 1 1 0	0 0 0 1

Tab. 3-1 Suma S i przeniesienie C dodawania jednobitowych liczb dwójkowych A i B

Zmienna S_i reprezentuje rezultat operacji, jej wartość jest sumą modulo 2 (exclusive OR) składników A_i, B_i i C_i. Zmienna Ci reprezentuje przeniesienie z pozycji młodszej sumatora wielopozycyjnego. C_i+1 jest przeniesieniem do pozycji starszej. C_i nie występuje w tzw. pólsumatorze, obecność C_i daje sumator pełny. Z wartości przedstawionych na Rys. 3-1 można określić wyrażenia logiczne dla półsumatora:

suma S_i = A_i-B_i + ~A_iB_i = A_i (+) B_i,

przeniesienie C_i+1 = A_iB_i.
Zasada działania sumatora pełnego została opisana siatkami Karnaugha przedstawionymi na Rys. 3-2.




Rys. 3-1 Sumator dwuargumentowy jednobitowy: a) symbol, b) siatka zależności dla sumy, c) siatka zależności dla przeniesienia

Z siatek tych otrzymujemy zależności:

suma

S_i = C_i(A_iB_i + ~A_i~B_i) + ~C_i(A_i~B_i + ~A_iB_i)= Ci ~(A_i (+) B_i) + ~C_i(A_i (+) B_i) = C_i (+) B_i (+) A_i,

przeniesienie

C_i+1 = A_iB_i + A_iC_i + B_iC_i.

Schemat sumatora pełnego (dwuargumentowego) z przeniesieniem z pozycji poprzedniej C_i oraz przeniesienie do pozycji wyższej C_i+1 przedstawiono na Rys. 3-3a. Sumator jednobitowy pokazany na Rys. 3-3b jest podstawową komórką występującą w sumatora średniej skali integracji: 480, 482 i 483.




Rys. 3-2 Schemat logiczny sumatora pełnego dwuargumentowego (a), jednobitowego (b)

Szczególnym przypadkiem sumatora jest układ realizujący odejmowanie dwu liczb dwójkowych. Wartości funkcji dla różnicy D i pożyczki V i-tej komórki sumatora odejmującego ilustruje tabela z Rys. 3-3.

Pożyczka Vi	Odjemna Ai	Odjemni Bi	Różnica Di	Pożyczka Vi+1
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 0 1 0 0 1	0 1 0 0 1 1 0 1




Rys. 3-3 Sumator jednobitowy odejmujący: a) symbol, b) siatka zależności, c) tabela zależności

Z siatki zależności przedstawionej na Rys. 3-3c znajdujemy wyrażenia logiczne dla sumatora odejmującego. Jak można zauważyć, różnica D_i jest identyczna z sumą S_i , natomiast różne są wyrażenia dla pożyczki V_i+1 i przeniesienia C_i+1. Jeśli jednak w wyrażeniach opisujących działanie sumatora odejmującego zamiast B_i wstawić ~B_i, a zamiast C_i wstawić ~V_i, otrzymujemy: C_i+1 = ~V_i+1, S_i=D_i.

Korzystając z tej własności, znajdujemy:

D_i = V_i (+)A_i(+)B_i,

~V_i+1=A_i~B_i + ~V_i(A_i+ ~B_i).

Sumator może być zatem stosowany jako układ odejmujący po dokonaniu powyższych przełączeń.

2. Sumatory wielobitowe równoległe.

Ze względu na sposób wytwarzania przeniesień dzielimy je na:

• sumatory z przeniesieniem szeregowym, zwane również sumatorami kaskadowymi albo iteracyjnymi,

• sumatory z przeniesieniem równoległym.

Sumator kaskadowy n-bitowy jest układem powstałym przez połączenie n sumatorów jednobitowych. Schemat blokowy takiego sumatora przedstawiono na Rys. 3-4. Przy sumowaniu liczb dodatnich wejście przeniesienia początkowego C₀ nie jest wykorzystywane (C₀=0).




Rys. 3-4 Schemat blokowy sumatora kaskadowego

W sumatorze kaskadowym wszystkie cyfry dodawanych liczb dwójkowych podawane są na sumator jednocześnie. Czas uformowania się wyniku zależy od prędkości propagacji sygnału przeniesienia przez kolejne komórki sumatora. W najbardziej niekorzystnym przypadku sygnał C musi przejść przez wszystkie komórki sumatora. Czas sumowania można znacznie skrócić przez zastosowanie sumatora z równoległym przeniesieniem. Sumator z przeniesieniem równoległym generuje wszystkie wartości przeniesień jednocześnie na podstawie wartości na poszczególnych bitach obu operandów. Przeniesienie C_i+1 = A_iB_i + A_iC_i + B_iC_i = A_iB_i + (A_i+B_i)C_i można wyrazić w postaci: C_i+1= G_i+T_iC_i, gdzie: G_i=A_iB_i, T_i=A_i+B_i.

Dla modułu czterobitowego i <{0,1,2,3}:

C₄=G₃+T₃G₂+T₃T₂G₁+T₃T₂T₁G₀+T₃T₂T₁T₀

lub C₄ = G + TC₀,
gdzie G= G₃+T₃G₂+T₃T₂G₁+T₃T₂T₁G₀; T=T₃T₂T₁T₀,

gdzie:

G - przeniesienie generowane w bloku,

T - sygnał warunkujący transmisję przeniesienia początkowego C₀.

Wyrażenie dla sumy: S_i = A_i (+) B_i(+)C_i można przekształcić do postaci:

S_i = C_i(+)~(A_iB_i)(A_i+B_i)= C_i (+) ~G_iT_i.

Układy wielobitowe (nx4 bity) montuje się, wykorzystując powyższy sumator oraz expander, zwany generatorem przeniesień równoległych (4182). Ze względów praktycznych (minimalizacja struktury logicznej) zarówno w sumatorze, jak i generatorze przeniesień równoległych zamiast zmiennych G i T występują ich negacje ~G i ~T. Ze wzrostem ilości bitów przewaga sumatora z przeniesieniami równoległymi nad sumatorem z przeniesieniami kaskadowymi staje się coraz bardziej widoczna. Omówione wyżej sumatory mogą wykonywać oprócz operacji arytmetycznych również operacje logiczne. Sumator z przeniesieniami równoległymi jest zawarty w czterobitowym elemencie scalonym 4181, zwanym jednostką arytmetyczno-logiczną.

1. Dodawanie i odejmowanie wielobitowe równoległe.

Operacji dodawania i odejmowania równoległego liczb wielobitowych dokonuje się za pomocą sumatorów wielobitowych. Dodawanie dwu liczb binarnych odbywa się przez dodanie poszczególnych pozycji binarnych, z uwzględnieniem przeniesienia z każdej pozycji. Przy zapisie binarnym liczb pozycja pierwsza jest znakiem liczby. Znak + oznacza się zerem, a znak - jedynką. Po bicie znaku następuje przecinek, a następnie zadana liczba binarna (przeniesienie z bitu znaku pominąć).

Przykłady operacji dodawania:

	+13	0,1101
	+2	0,0010
	+15	0,1111

	-13	1,01101
	-7	1,00111
	-20	0,10100

Liczba pozycji sumatora jest określona na podstawie wyniku dodawania, nie może bowiem wystąpić jego przepełnienie. Podczas dyskusji odejmowania jednobitowego stwierdzono bardzo istotną zależność, że odejmowanie polega na dodawaniu negacji ( uzupełnienia do 1) odjemnika. Zasada ta jest również podstawą odejmowania wielobitowego. Operacje dodawania i odejmowania są zwykle realizowane w bloku arytmetycznym wykonującym też operacje mnożenia i dzielenia. W niniejszym rozdziale zostaną omówione trzy podstawowe algorytmy dodawania i odejmowania o różnym stopniu złożoności tych operacji.

1. Dodawanie w zapisie "znak- moduł".

Operacje dodawania i odejmowania sprowadzono tu do operacji dodawania. Wyróżnia się trzy przypadki dodawania:

1. dodawanie liczb o jednakowych znakach:




	+13	0,01101
	+7	0,00111
	+15	0,10100
	-13	1,01101
	-7	1,00111
	-20	0,10100




2. dodawanie liczb o przeciwnych znakach; moduł dodajnej większy od modułu dodajnika:




	+13	0,01101
	-7	1,00111
	+15	0,10100
	-13	1,01101
	+7	1,00111
	-6




do modułu dodajnej dodajemy moduł uzupełnienia do 1 (negację) dodajnika




01101

11000

00101

00110

01101

11000

00101

1

00110




wynikowy dodawania przypisujemy znak dodajnej; otrzymujemy:




	+6	0,00110
	-6	1,00110




3. dodawanie liczb o przeciwnych znakach; moduł dodajnika większy od modułu dodajnej:




	+10	0,01010
	-13	1,01101
	-10	1,01010
	+13	0,01101




do modułu dodajnej dodajemy moduł uzupełnienia do 1 dodajnika, wynik otrzymuje znak dodajnika.




01010

10010

11100

01010

10010

11100




z braku przeniesienia cyklicznego otrzymany wynik należy uzupełnić do 1 i nadać znak dodajnika.




	-3	1,0011
	+3	0,00011




2. Dodawanie w zapisie "uzupełnień do 1"

Dodawanie w zapisie "uzupełnień do 1" różni się od poprzedniej metody tym, że wszystkie liczby ujemne są rejestrowane w zapisie "dopełnień do 1" i dodawane wraz z bitem znaku. W metodzie tej wyróżniono cztery przypadki:

1. dodawanie liczb dodatnich jest takie samo jak w poprzedniej metodzie;

2. dodawanie liczb ujemnych: liczby ujemne są przedstawione w zapisie "uzupełnień do 1" , dodawanie odbywa się wraz z bitem znaku:

	-10	1,10101
	-13	1,10010
		1,00111
		1
		1,01000

wynikiem ostatecznym jest uzupełnienie do 1 modułu otrzymanej liczby z zachowaniem znaku;

dostajemy:

-23

1,0111

3. dodawanie liczb o przeciwnych znakach (wynik dodatni) :

	-10	1,10101
	+13	0,01101
		0,00010
		1
	+3	0,00011

4. dodawanie liczb o przeciwnych znakach (wynik ujemny):

Otrzymany wynik jest uzupełnieniem do 1 modułu otrzymanej liczby z zachowaniem znaku:

	+10	0,10101
	-13	1,01101
	-3	1,00011

3. Dodawanie w zapisie " uzupełnień do 2"

Podczas dyskusji nad zasadami odejmowania jednobitowego stwierdzono bardzo istotną zależność, a mianowicie odejmowanie polega na dodaniu negacji odjemnika (~B_i). Drugi wniosek dotyczył pożyczki, a więc w miejsce przeniesienia Ci sumatora należy podać wartość ~V_i. Oznacza to, że pierwsza komórka sumatora w czasie odejmowania ma na wejściu Co jedynkę logiczną, czyli do najmniej znaczącej pozycji sumatora dodajemy wartość 1. Zasada ta została wykorzystana w algorytmie "uzupełnień do 2" . Liczby ujemne są zapisywane jako dopełnienie do 1 modułu plus 1 na pozycji najmniej znaczącej. Metoda ta sprowadza się właściwie do jednego przypadku: dodawania liczb z dowolnym znakiem. Liczby dodatnie są dodawane podobnie jak w poprzednich metodach.

Liczby ujemne:

	-10	1,10101
		1
	-10	1,10110
	-13	1,10011
		1,01001

bez dodawania przeniesienia cyklicznego.

W przypadku gdy otrzymany wynik ma znak ujemny, odczyt wartości ostatecznej polega na uzupełnieniu do 2 modułu z zachowaniem znaku. Dostajemy:

-23

1,10111

Dodawanie liczb o różnych znakach:




	+10	0,01010
	-13	1,01101

wynik ujemny: znajdujemy uzupełnienie do 2 modułu, otrzymamy

	-3	1,00011
		1,11101
	-10	1,01010
	+13	0,01101
		0,00011

bez dodawania przeniesienia cyklicznego




4. Porównanie zapisów.

W operacjach dodawania i odejmowania najprostszy jest zapis "uzupełnień do 2" ze względu na prostotę układów wykonujących te operacje. Pozostałe zapisy są mniej wygodne, przy czym zapis "znak-moduł" pozwala na prostą realizację operacji mnożenia i dzielenia. Z kolei zapis "uzupełnień do 2" jest przypadkiem pośrednim (kompromisowym). Wybór zapisu będzie oczywiście rzutował na konstrukcję układów wykonujących wspomniane operacje arytmetyczne.

2. Komparatory

Komparatorem cyfrowym nazywamy układ służący do porównywania dwóch słów dwójkowych n-bitowych. Zgodność wszystkich pozycji porównywanych słów jest sygnalizowana wartością 1 na wyjściu komparatora. Czyli inaczej : komparator n-bitowy F_A=B realizuje funkcję logiczną:

F_(A=B)= (A₀B₀+ ~A₀~B₀) * (A₁B₁+ ~A₁B₁)...(A_n-1B_n-1+ ~A_n-1B_n-1).




Rys. 3-5 Schemat logiczny przykładowego rozwiązania komparatora

Przykład realizacji komparatora przedstawiono na Rys. 3-5. Do budowy tego komparatora użyto bramek NAND z pełnym wyjściem bramek NAND z otwartym kolektorem. Komparator n-bitowy można zaprojektować jako zwykły układ kombinacyjny lub prościej jako układ iteracyjny ( znacznie wolniejszy w działaniu). Komparatory oprócz sprawdzania, czy A=B, mogą dokonywać sprawdzenia A>B, A<>B itp. Zależnie od rodzaju porównania różna będzie konstrukcja komparatora. Niniejsze ćwiczenie omawia zasady projektowania obu podstawowych wersji komparatora wielobitowego: komparatora kombinacyjnego oraz iteracyjnego. Komparator kombinacyjny czterobitowy można zaprojektować na podstawie Tab. 3-2.

Wejścia				Wyjścia
A4 , B4	A3 , B3	A2 , B2	A1 , B1	A > B	A < B	A = B
A4 > B4 A4 < B4 A4 = B4 A4 = B4 A4 = B4 A4 = B4 A4 = B4 A4 = B4 A4 = B4	- - A3 > B3 A3 < B3 A3 = B3 A3 = B3 A3 = B3 A3 = B3 A3 = B3	- - - - A2 > B2 A2 < B2 A2 = B2 A2 = B2 A2 = B2	- - - - - - A1 > B1 A1 < B1 A1 = B1	1 0 1 0 1 0 1 0 0	0 1 0 1 0 1 0 1 0	0 0 0 0 0 0 0 0 1

Tab. 3-2 Zasada działania komparatora kombinacyjnego

Przyjmiemy oznaczenia:

X_i=1 dla A_i>B_i

Y_i=1 dla A_i=Bi

Z_i=1 dla A_i<B_i

Oraz

A={A₀,A₁,A₂,A₃},

B={B₀,B₁,B₂,B₃}.

x_we, y_we, z_we - wynik porównania na młodszych pozycjach komparatora n-bitowego,

x_wy,y_wy, z_wy - wynik porównania na wyjściu komparatora.

Z tablicy 11.1 można otrzymać wyrażenia opisujące działanie komparatora:

x_wy= x₃+y₃x₂ + y₃y₂x₁ + y₃y₂y₁x₀ + y₃y₂y₁y₀x_we~y_we~z_we,

y_wy = y₃y₂y₁y₀~x_we y_we ~z_we,

z_wy = z₃ + y₃z₂ + y₃y₂z₁ + y₃y₂y₁z₀ + y₃y₂y₁y₀ ~x_we~y_we z_we.

Uzyskaliśmy czterobitową komórkę komparatora kombinacyjnego (Rys. 3-6), za pomocą której da się budować komparatory o większej liczbie bitów.




Rys. 3-6 Komparator czterobitowy kombinacyjny: a) schemat blokowy, b) symbol

W układzie występuje element Ki będący komóką jednobitową komparatora. komórkę Ki opisują następujące funkcje kombinacyjne: x_i = A_i~B_i,

y_i = A_iB_i + ~A_i~B_i,

z_i = ~A_iB_i.

Schemat blokowy komparatora iteracyjnego przedstawiono na Rys. 3-7. Rys. 3-8. zawiera siatkę zależności i-tej komórki komparatora iteracyjnego. Wyjście C_i+1 komórki jest określone zależnością:




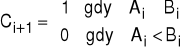
Z siatki zależności można określić funkcję logiczną i-tej komórki komparatora:

C_i+1= A_i~B_i + C_i~B_i + C_iA_i.




Rys. 3-7 Schemat blokowy komparatora iteracyjnego czterobitowego




Rys. 3-8 Siatka zależności dla i-tej komórki komparatora iteracyjnego

• LITERATURA

[1] Badźmirowski, J. Pieńkos, W. Piestrzyński: Cyfrowe układy MOS LSI, Warszawa WKiŁ 1979.

[2] Binkowski, H. Krzyż, J. Piecha: Elektronika analogowa i cyfrowa w zadaniach. Katowice Wydawnictwo Uniwersytetu śląskiego 1981.

[3] Kalisz: Cyfrowe układy scalone w technice systemowej. Warszawa MON 1977.

[4] Millman, C. Halkias: Układy scalone analogowe i cyfrowe. Warszawa WNT 1976.

[5] Misiurewicz, M. Grzybek: Półprzewodnikowe układy logiczne TTL. Warszawa WNT 1979.

[6] Eadie: Nowoczesne maszyny i systemy cyfrowe. Warszawa WNT 1975.

[7] Wagner: Projektowanie urządzeń cyfrowych. Warszawa WNT 1978.

[8] Mano: projektowanie systemów logicznych maszyn cyfrowych. Warszawa WNT 1975.

Instrukcja do ćwiczenia 7 11

---