Temat: REGULATORY PID
Zadaniem regulatora PID jest utrzymanie wartości wyjściowej na określonym poziomie, zwanym wartością zadaną. Składa się z członu proporcjonalnego P o wzmocnieniu kp, całkującego I o czasie zdwojenia Ti oraz różniczkującego D o czasie wyprzedzenia Td.
Regulator P (proporcjonalny). W regulatorze tym sygnał wyjściowy jest proporcjonalny do wejściowego. Na podstawie sygnału podawanego na wejście regulatora, wytwarza on proporcjonalny sygnał sterujący, przy czym celem jest utrzymanie wartości wyjściowej układu na pewnym z góry zadanym poziomie, który jest zwany wartością zadaną (dążenie do eliminacji uchybu regulacji). Układy regulacji z regulatorem typu P charakteryzują się niezerowym uchybem ustalonym.
Regulator I (całkujący). Regulator I umożliwia realizację regulacji astatycznej, gdy uchyb jest równy 0. Z obiektami astatycznymi może tworzyć niestabilne układy regulacji. Może być stosowany głównie w obiektach statycznych charakteryzujących się powolnymi zmianami obciążenia.
Regulator D (różniczkujący). Przeciwdziała szybkim zmianom sygnału błędu, co wpływa stabilizująco na działanie układu regulacji. Pozwala to na zwiększenie intensywności działania pozostałych parametrów regulatora.
Regulatory proporcjonalno - całkująco - różniczkujące są regulatorami uniwersalnymi - wzmacniają, całkują i różniczkują odchyłkę regulacji. Sygnał wyjściowy regulatora PID jest proporcjonalny do sumy sygnału wejściowego, jego całki oraz jego pochodnej. Jedna część odpowiedzi skokowej regulatora PID jest proporcjonalna (P) do odchyłki regulacji, druga (I) jest całką z odchyłki regulacji, trzecia (D) - pochodną z odchyłki regulacji względem czasu. Regulator PID stosuje się zazwyczaj do obiektów poddawanych wpływom zakłóceń o dużych i gwałtownych zmianach. Regulator ten stosuje się w przypadku gdy mamy do czynienia ze stałą wartości wielkości zadającej - a więc w układach regulacji stałowartościowej, np. układach regulacji temperatury.
Badanie podstawowych członów i układów regulatorów PID
Podczas ćwiczenia badano podstawowe człony i układy regulatorów PID. Podawano wymuszenia prostokątne i trójkątne. Dla poszczególnych członów przy różnych nastawach zaobserwowano:
P
Wymuszenie prostokątne
Zmiana f - zmienia się f wymuszenia i wyjścia, amplituda jest stała
Zmiana Kp - zmienia się amplituda na wyjściu, do wartości 10 V
Wymuszenie trójkątne
Zmiana f - zmiana f na wejściu i wyjściu, amplituda nie ulega zmianie
Zmiana Kp - zmiana amplitudy
I
Wymuszenie prostokątne
Zmiana f - zmiana f i amplitudy, przy wzroście f - na wyjściu zwiększa się f i amplituda
Zmiana KI - zmienia się amplituda, przy minimalnej wartości KI charakterystyka jest zbliżona do linii prostej
Wymuszenie trójkątne
Zmiana f - zmiana f i amplitudy na wejściu i wyjściu (przebieg sinusoidalny)
Zmiana KI - zmiana f i amplitudy na wyjściu
D
Wymuszenie prostokątne
Zmiana f - zmienia się f wymuszenia i wyjścia
Zmiana KD - zmienia się amplituda na wyjściu
Wymuszenie trójkątne
Zmiana f - zmiana amplitudy
Zmiana KD - przebieg prostokątny
PI
Wymuszenie prostokątne
Zmiana f - zwiększa się amplituda człony całkującego (wraz ze wzrostem czasu trwania wymuszenia, zwiększa się amplituda, ponieważ musi zostac scałkowana długość tego wymuszenia)
Zmiana Kp - zmienia się człon proporcjonalny
Zmiana KI - zmienia się nachylenie charakterystyki
Wymuszenie trójkątne
Zmiana f - zwiększa się f na wejściu i wyjściu, przy znacznym wzroście f - zwiększa się amplituda
Zmiana Kp - zwiększa się amplituda
Zmiana KI - odkształca charakterystykę, całkując wymuszenie trójkątne
PD
Wymuszenie prostokątne
Zmiana f - zmienia się f wymuszenia i wyjścia, amplituda jest stała
Zmiana Kp - zmienia się amplituda
Zmiana KD - zmiana amplitudy, przy minimalnym KD - minimalna amplituda
Wymuszenie trójkątne
Zmiana f - zmiana f na wejściu i wyjściu
Zmiana Kp - zmiana amplitudy
Zmiana KD - zmiany niewidoczne
Badanie układów regulacji regulatora P
Układ równań:
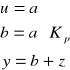
Badanie wzmocnienia
u |
-3,6 |
-2,1 |
-0,92 |
1,11 |
2,3 |
3,6 |
Kp średnie = 2,646 |
y |
-9,55 |
-5,5 |
-2,45 |
2,95 |
6,08 |
9,51 |
|
Kp |
2,653 |
2,619 |
2,663 |
2,658 |
2,643 |
2,642 |
|
Badanie zakresu proporcjonalności regulatora P
u = 0,27 |
z = 0 |
|
|
Kp minimum |
y = 0,46 |
Kp min = 1,70 |
Xp min = 58,82 % |
Kp maximum |
y = 5,59 |
Kp max = 20,70 |
Xp max = 4,83 % |
Wyznaczanie transmitancji układu regulacji
|
u = 0,28 |
z = 0,08 |
a = 0,27 |
|
|
b = 0,54 |
|
|
y = 0,62 |
|
|
Obliczam Gw
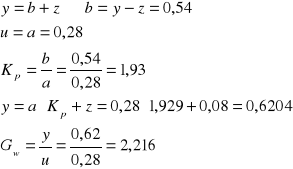
Badanie kompensacji zakłóceń
Kp = 2 |
u = 0,28 |
z = 0 |
y0 = 0,53 |
y=0,56 |
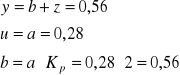
Kp = Kp(a) |
u = u(a) |
z = 0,09 |
y = 0,62 |
y=0,65 |
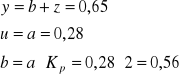
Kp = 2 |
u = u(a) |
z = z(b) |
y = y0=0,53 |
y=0,56 |
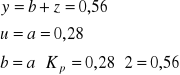
Badanie zamkniętego układu regulacji
Kp = 2,41 u = 0,62 z = 0 |
|
a = 0,34 |
H = 0,33 |
b = -0,82 |
Gwz = 1,32 |
c = 0,81 |
εz = 0,2 |
d = 0,27 |
Gw = 1,34 |
y = -0,82 |
εw = 0,21 |
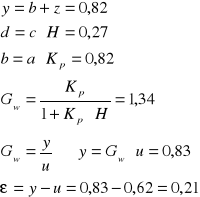
Badanie wpływu transmitancji sprzężenia zwrotnego na przebieg regulacji
Kp = 2,44 u = 0,62 z = 0 |
|
a = 0,27 |
H0 = 0,56 |
b = -0,66 |
Gwz → 1 |
c = 0,62 |
εz → 0 |
d = 0,35 |
Gw = 1,03 |
y → u |
εw = 0,02 |
Badanie wpływu zakłóceń na przebieg regulacji
Kp = 2,47 u = 0,62 z = 0,11 |
|
a = 0,23 |
H = H0 |
b = -0,57 |
Gwz = 1,1 |
c = 0,68 |
εz = 0,06 |
d = 0,38 |
Gw = 1,04 |
y1 = 0,68 |
εw = 0,03 |
Wnioski
Celem ćwiczenia było badanie podstawowych członów i układów regulatora PID. Podczas ćwiczenia obserwowano przebiegi wymuszeń i odpowiedzi przy zmianach częstotliwości oraz różnych wartościach nastaw.
Wykreślona charakterystyka y = f(u), pozwala stwierdzić, że napięcie na wejściu jest wprost proporcjonalne do napięcia na wyjściu układu. Zakres proporcjonalności przy minimalnej wartości Kp jest duży i wynosi 58,82%. Zakres proporcjonalności przy maksymalnej wartości Kp wynosi około 4,83%.
Następnie badano zamknięty układ regulacji. Wartości mierzone porównywano z wartościami wyznaczonym. Zauważono, że istnieje niewielka różnica, spowodowana niedokładnością pomiaru oraz wpływem zakłóceń.