GRUPA A

1.Co to jest równoważność układów (A)=(B)

-podstawowa definicja równoważności:

Dane układy sił (A) i (B) nazywamy równoważnymi wtw gdy wykonując na jednym z nich skończoną liczbę przekształceń elementarnych typu α i β w wyniku otrzymamy układ drugi.

Relacja równoważności jest:

- zwrotna (A)=(A)

- symetryczna jest (A)=(B) to (B)=(A)

- przechodnia (A)=(B) i (B)=(C) to (A)=(C)

Co to jest redukcja układów

W związku z możliwością identycznych działań użytych układów sił działających na to samo ciało pojawia się zagadnienie zastąpienia jednego układu sił innym na ogół prostszym, ale o identycznym działaniu, zagadnienie to nosi nazwę redukcji układu.

Tw.

Dowolny układ sił jest równoważny układowi złożonemu z wektora sumy tego układu zaczepionego w dowolnie wybranym biegunie oraz pary sił o momencie układu obliczonego momentu względem tego bieguna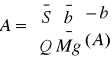

2.Co to jest energia mechaniczna(praca mechaniczna) i jaki ma związek z polem zachowawczym.

En.mechaniczna to suma energii potencjalnej i kinetycznej

-E(t)=Ek(t) +Ep(t)

-(praca)L=ΔEk+ ΔEp= ΔE

-praca siły czynnej działającej na PM w polu potencjalnym w danym przedziale czasu jest równa przyrostowi energii mechanicznej w tym przedziale czasu.

-w układzie zachowawczym Em ma wartość stałą, jest to tzw.zasada zachowania Em.

3.Rzut wektora
(ax,ay,az) na wektor
(bx,by,bz)

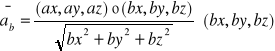
4.Podstawowe i zastępcze równania równowagi statycznej dla układu płaskiego.

podstawowe

Zastępcze:

5.Reakcje więzów

6. Warunek geometrycznej niezmienności, przykłady

V=3T-p-2b-3, b-przeguby, 2b-równań więzów, T-tarcze, p-pręty (wahacze),

V=3(T-1)-(p+2b) , 3T-stopni swobody

3(T-1) -liczba stopni swobody układu względem układu (tarczy) odniesienia

(p+2b) -liczba więzów (więzi)- liczba więzów między tarczami

V>0 -więcej stopni swobody niż równań więzów- układ geometrycznie zmienny

V=0 -liczba stopni swobody i liczba więzów są sobie równe, układ może być geometrycznie niezmienny

V<0 -układ przesztywniony i więcej więzów niż możliwości ruchowych może być geometrycznie niezmienny

V≤0 -jest tylko warunkiem koniecznym geometrycznej niezmienności

7.Układy współrzędnych i ich równania toru:

-kartezjański: x_i=f_i(t), i=1,2,3

-biegunowy: r=Ψ₁(t); φ= Ψ₂(t)

-walcowe: ρ= φ₁(t); φ₁= φ₂(t); z= φ₃(t)

-naturalne:

8.Hodograf prędkości i przyśpieszenia:

Jest to miejsce geometryczne końców kolejnych wektorów prędkości odkładanych od dowolnie wybranego bieguna. Wektor przyśpieszenia ā_i jest styczny do hodografu prędkości
w punkcie
_i.

9.Oś środkowa układu sił- jest to miejsce geometryczne punktu względem których wektor momentu jest równoległy do wektora sumy lub moment jest równy zero.

-równanie osi środkowej układu

10.Wyznacz siłę w układzie biegunowym

-siły w układzie biegunowym wyznaczamy za pomocą równania dynamiki ruchu.

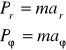
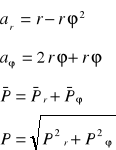
GRUPA B

Zad. 1 Zredukować układ A do punktu 0.

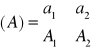
zredukować 0(0,0)

= O

= O

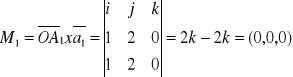
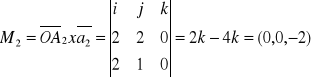
Mg=(0,0,-2)

R=0

Zad.2 Metoda Rittera

Kratownice możemy zawsze podzielić przekrojem na dwie tarcze T₁ i T₂. Jeżeli przekrój przecina 3 nie przecinające się w jednym punkcie pręty to nazywamy go przekrojem Rittera. Rozcinając przekrojem pręty to znaczy że usuwamy więzy jakimi są te pręty- ich reakcje to siły w rozciętych prętach.

Punkt Rittera- jest punktem w którym przecinają się kierunki dwóch pozostałych rozciętych prętów.

3.Energia kinetyczna

,zatem L=Ek(t2)-Ek(t1)= ΔEk

L=ΔEk

Zasada równoważności pracy i energi kinetycznej.

Praca siły czynnej działającej na punkt materialny w danym przedziale czasu jest równa przyrostowi energii kinetycznej w tym przedziale czasu.

4.Chwilowy środek obrotu.Co to jest i jak go wyznaczamy.

W płaszczyźnie kierowniczej znaleźć można taki punk C, którego prędkość chwilowa jest równa 0.

czyli jest także

Punkt C nosi nazwę chwilowego środka obrotu

5.WKW geometrycznej niezmienności układu złożonego z dwóch tarcz.

V=3T-p-2b-3≤0 oraz aby kierunki prętów między nimi nie przecinały się w jednym właściwym lub niewłaściwym punkcie.

WKW g. niezmienności układu trzech tarcz jest aby V=3T-p-2b-3≤0 oraz nie wystąpiły przypadki przedstawione na rys.

6.Więzy

7.Równania równowagi statycznej dla przestrzennego układu sił

Sumy rzutów sił na osie x1,x2,x3 muszą być równe 0.

Sumy momentow względem x1,x2,x3 muszą być równe 0.

Zad. 8 Środek równoległego układu wektorów.

Ciału sztywnemu przyporządkuje się pewien szczególny punkt „C” zwany środkiem masy ciała sztywnego. W punkcie zaczepiona jest siła ciężkości ciała G=m*g skierowana zawsze w jedną stronę bez względu na położenie ciała w przestrzeni. Punkt „C” jest środkiem równoległego układu sił
zatem

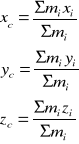
czyli:
;
;
gdzie:

z powyższych wzorów wynika

;
;

9.Statyczne i kinematyczne schematy przegubów dwustronnych

-narysować schematy 3 podpór:przesuwnej,nieprzesuwnej i utwierdzenia w ścianie.

10.Kiedy 3 wektory mogą być wektorami bazy? Kiedy są ortogonalne?

-3 wektory są ortogonalne kiedy ich wyznacznik jest różny od zera.

a(ax,ay,az)

b(bx,by,bz)

c(cx,cy,cz)

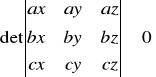
wtedy są ortogonalne!!!

-3 wektory mogą być wektorami bazy gdy nie są do siebie równoległe tzn.gdy ich wyznacznik jest różny od zera.

(inna wersja)wektory bazy-kiedy trzeci z nich nie jest kombinacją liniową pozostałych dwóch.

ZADANIA

Zadanie 1.

Rozwiązanie

Układ znajduje się w polu potencjalnym sił ciężkości.

Zasada zachowania energii.

,

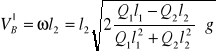
Zadanie 2.

Rozwiązanie

Na pręt działają dwie siły zewnętrzne, siła ciężkości Q i siła reakcji R.

Do każdego elementu dm przykładamy siłę bezwładności.

;
dy

;
dy

;

Układ sił działających na pręt jest w równowadze.

Po wykonaniu całkowania jest:

Zatem:

Czyli:

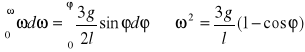
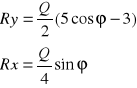
Zadanie 3.

Rozwiązanie

Zadanie 4.

Rozwiązanie: Sz: α,S,

D:m,ω