A 3.02.03

Egzamin z algebry liniowej

Imię i nazwisko:

Numer grupy:

Zad. 2 (7p.) Rozwiąż równanie:

Zad. 3 (6p.) Niech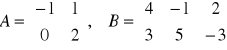
. Jeśli to możliwe oblicz
.

Zad. 4 (8p.) Przeprowadź dyskusję rozwiązalności układu równań w zależności od wartości parametru
:

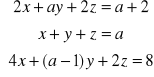
Zad. 5 (8p)

1. Stosując metodę Gaussa rozwiąż układ równań:

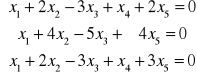
2. Wyznacz bazę i wymiar przestrzeni rozwiązań tego układu.

3. Znajdź współrzędne wektora (-3, 2, 1, 2, 0) w wyznaczonej bazie.

Zad. 6(7p.)

Przekształcenie liniowe
ma w bazach standardowych macierz: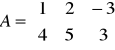
.

1. Znajdź wzór jakim określone jest
   .

2. Wyznacz bazę obrazu
   .

Zad. 7(8p.)

Niech
będzie przekształceniem liniowym. Znajdź wartości własne
i wektor własny dla jednej z nich.

---