KINETYCZNA TEORIA GAZÓW
Kinetyczna teoria gazów to nauka o budowie i własnościach fizycznych gazów oparta na statystycznych metodach badania. (prawa mechaniki stosuje się tu statystycznie- liczba atomów czy cząsteczek w układach makroskopowych jest tak duża, że wielkości średnie dają wystarczająco dobre przybliżenie; wszystkie zmienne termodynamiczne dadzą się wyrazić jako średnie parametrów atomowych)
Opiera się na założeniach dla gazu doskonałego:
a) molekuły (drobiny) z których gaz się składa, zachowują się jak punkty matematyczne: nie posiadają objętości (w porównaniu z całkowitą objętością zajmowaną przez gaz, jest ona zaniedbywalna), a posiadają masę i prędkość, która
w każdym danym kierunku jest taka sama.
Statystycznie, w każdym kierunku porusza się taka sama liczba drobin.
b) poza chwilą, w której następuje zderzenie, molekuły nie oddziałują ze sobą,
c) zderzenia są doskonale sprężyste (spełnione są zasady zachowania energii, pędu i momentu pędu, czyli wszystkie te wielkości przed i po zderzeniu pozostają takie same) i ich czas trwania wynosi 0.
RÓWNANIE CIŚNIENIA GAZU W NACZYNIU
W ŚWIETLE TEORII KINETYCZNEJ
Molekuły gazu w naczyniu nieustannie zderzają się między sobą (charakter tych zderzeń jest całkowicie przypadkowy). Oprócz tego uderzają w ścianki naczynia; ciśnienie jest stosunkiem składowej normalnej siły, z jaką uderzają w ściankę do pola powierzchni tej ścianki. Ponieważ zakładamy, że gaz jest doskonały i cząsteczki między sobą zderzają się doskonale sprężyście, zderzenia te nie wpływają na wartość ciśnienia gazu (częstość czy siłę uderzeń w ścianki naczynia).
(Wyprowadzając podstawowe równanie dla ciśnienia gazu, dla uproszczenia obliczeń wybieramy naczynie w kształcie sześcianu.)
S- pole powierzchni ściany sześcianu
n0- liczba cząsteczek w jednostce objętości
m- masa cząsteczki
Vx, Vy, Vz- składowe prędkości każdej cząsteczki
n1, n2..., ni- liczba cząsteczek w jednostce objętości o składowej Vx1, Vx2..., Vxi
Zmiana pędu pojedynczej cząsteczki o składowej Vxi wskutek zderzenia ze ścianą wynosi 2mVxi (po zderzeniu zmienia się zwrot prędkości, ale jej wartość i kierunek pozostają bez zmian).
W czasie ∆τ w ścianę uderza ½SVxi∆τni cząsteczek o prędkości Vxi (w objętości SVxi∆τ jest ich SVxi∆τni; połowa cząsteczek porusza się jedną stronę, połowa w drugą).
Zmiana pędu tych cząsteczek = popędowi siły wywieranej na ścianę przez cząsteczki , czyli:
2mVxi · ½SVxi∆τni = Fi∆τ
ciśnienie wywierane przez te cząstki:
pxi = Fi/S = nimV2xi
px = Σpxi = ΣnimV2xi = mΣniV2xi,
średni kwadrat prędkości ![]()
2x = ΣniV2xi/n0
px = mn0![]()
2x
Ze względu na dużą liczbę molekuł i ich bezładny ruch:
![]()
2x = ![]()
2y = ![]()
2z
Ponieważ ![]()
2 = ![]()
2x + ![]()
2y + ![]()
2z
Więc ![]()
2 = 3![]()
2x;
px = ⅓mn0![]()
2; ponieważ ρ = mn0, to
px = ⅓ ρ![]()
2
lub w innej postaci: pυ = ⅔Wk,
Wk - sumaryczna energia kinetyczna ruchu postępowego N znajdujących się w naczyniu cząsteczek,
υ - objętość właściwa
M = Nm - masa gazu
Stosując równanie stanu gazu można napisać, że
RT = ⅔ ⋅ ½ ⋅ M![]()
2
RT = ⅓ M![]()
2
Stąd wniosek, że ponieważ średni kwadrat prędkości jest wprost proporcjonalny do temperatury bezwzględnej i odwrotnie do masy gazu (a więc i do masy cząsteczki),
to im wyższa temperatura, tym szybciej cząsteczki się poruszają, a cięższe cząsteczki poruszają się wolniej niż lżejsze; w temperaturze zera bezwzględnego ruch drobin ustałby.
Według teorii kinetyczno - molekularnej materii (dotyczącej wszystkich stanów skupienia, nie tylko gazów), wszystkie drobiny materii nieustannie się poruszają ruchem cieplnym (termicznym).
Ciśnienie gazu w naczyniu jest więc makroskopowym przejawem tego ruchu.
ROZKŁAD MAXWELLA
Dotyczy najbardziej prawdopodobnego rozkładu prędkości w dużej liczbie cząsteczek gazu.
Jest to rozkład stacjonarny (dla gazów znajdujących się w stanie równowagi termodynamicznej). Zakładając całkowitą bezładność ruchu molekuł:
ƒ(V) = dNv/dV
ƒ(V) = 4πN(m/2πkT)3/2 V2 exp(- mV2/2kT)
ƒ (V)- określa, jaka liczba molekuł gazu z ogólnej liczby jego molekuł w jednostce objętości ma w danej temperaturze prędkości zawarte w przedziale (V, V+dV).
Nv - liczba molekuł o prędkości V
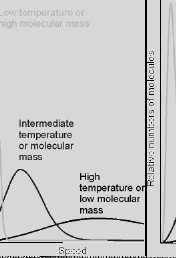
Rys.1. Krzywe rozkładu prędkości molekuł dla różnych temperatur T1 <T2 <T3
Vpr - prędkość najbardziej prawdopodobna
(krzywa nie jest symetryczna względem Vpr, ponieważ najniższa prędkość może wynosić 0, a najwyższa prędkość, jaką może osiągnąć cząsteczka nie jest ograniczona).
Wraz ze wzrostem temperatury bezwzględnej rośnie najbardziej prawdopodobna prędkość cząsteczek, a liczba cząsteczek poruszających się z tą prędkością maleje.
Gdy V = Vpr, to ƒ = ƒmax, czyli ![]()
= 0
![]()
(V2 exp(-mV2/2kT)) = 0
V = Vpr = ![]()
kT/m
ROZKŁAD CZĄSTECZEK W POTENCJALNYM POLU SIŁ (rozkład Boltzmanna)
Zwykle gaz znajduje się w potencjalnym polu przyciągania Ziemi. Gdyby tego pola nie było, powietrze atmosferyczne rozproszyłoby się po Wszechświecie. Z drugiej strony, jeśliby ruch cieplny nie istniał, to cząsteczki powietrza atmosferycznego spadłyby na powierzchnię Ziemi. Przyciąganie ziemskie i ruch cieplny prowadzą do stanu stacjonarnego gazu, przy którym ze wzrostem wysokości nad powierzchnią Ziemi maleje koncentracja i ciśnienie gazu.
Jeśli gaz (lub inny układ cząsteczek) znajduje się w zewnętrznym potencjalnym polu sił, to rozkład cząstek w objętości opisuje prawo rozkładu Boltzmanna. Rozkład Boltzmanna ustala liczbę cząstek dn (x, y, z), których współrzędne znajdują się w przedziałach od
x do x + dx, od y do y + dy, od z do z + dz; dn(x, y, z) jest więc liczbą cząstek znajdujących się w elementarnej objętości dV = dxdydz.
Rozkład Boltzmanna ma postać: dn (x, y, z) = const · exp ( -wp(x, y, z)/kT )dxdydz,
wp (x, y, z) - energia potencjalna cząstki w zewnętrznym polu sił,
k - stała Boltzmanna; k = R/NA
Wartość const wyznaczamy z warunku normowania
∫ dn = n0
Gęstość gazu, równa ρ = m ![]()
maleje więc wykładniczo wraz z wysokością:
ρ = const∙ exp (-mgh/kT)
Wartość const można wyznaczyć z warunku ρ = ρ0 = const dla h = 0.
Zmiany gęstości gazu lub jego ciśnienia w zależności od wysokości h wyraża wzór barometryczny:
ρ = ρ0exp (-mgh/kT)
p = p0exp (-mgh/kT)
ŚREDNIA DROGA SWOBODNA CZĄSTECZEK GAZU, ZASADA EKWIPARTYCJI ENERGII, ENERGIA WEWN. GAZU DOSKONAŁEGO
Średnia liczba zderzeń
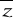
![]()
= ![]()
πd2n0![]()
, gdzie d- efektywna średnica cząsteczki,
n0 - liczba molekuł w jednostce objętości gazu,
![]()
- prędkość średnia
Średnią drogą swobodną
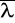
nazywamy średnią odległość, którą cząsteczka pokonuje bez zderzenia. Wielkość ta charakteryzuje cały zbiór molekuł gazu przy zadanych p i T.
Gdyby cząsteczki były punktowe, nie zderzałyby się w ogóle, a ![]()
byłaby nieskończona. Gdyby cząsteczek niepunktowych było tak wiele, że wypełniałyby całą przestrzeń, ![]()
wynosiłaby 0; zatem ![]()
musi zależeć zarówno od rozmiarów cząsteczek, jak ich liczby w jednostce objętości.
Wartość średnia drogi, jaką cząsteczka pokonuje w jednostce czasu, jest liczbowo równa ![]()
, dlatego ![]()
= ![]()
⋅ ![]()
.
![]()
= ![]()
/ ![]()
= ![]()
Kinetyczna teoria gazów zakłada, że jedyny wkład do energii całkowitej cząsteczki pochodzi od EK.
Zasada ekwipartycji energii: na każdy stopień swobody cząsteczki (stopień swobody to niezależny sposób absorpcji energii; inaczej, jest to liczba niezależnych ruchów, jakie może wykonywać cząsteczka jako układ mechaniczny) przypada średnio taka sama ilość energii kinetycznej równa kT/2. Jeśli cząsteczka ma i stopni swobody, jej średnia energia kinetyczna jest równa ![]()
= ikT/2
Zasada ekwipartycji energii oznacza równoprawność wszystkich stopni swobody cząsteczek- wszystkie wnoszą jednakowy wkład do średniej energii molekuły.
Cząsteczka gazu jednoatomowego ma 3 stopnie swobody (związane z jej ruchem postępowym wzdłuż trzech wyróżnionych w przestrzeni kierunków), czyli jej średnia energia wynosi
![]()
= ![]()
kT
Cząsteczka gazu dwuatomowego ma 5 stopni swobody (oprócz 3 stopni swobody ruchu postępowego ma jeszcze 2 stopnie swobody ruchu obrotowego, wokół dwóch osi. Moment bezwładności cząsteczki liczony przy obrocie wokół trzeciej osi jest znikomo mały i obrót taki nie daje znaczącego wkładu do energii całkowitej).
Cząsteczki składające się z trzech i więcej atomów mają 6 stopni swobody.
Energia wewnętrzna gazu wieloatomowego jest energią kinetyczną wszystkich rodzajów ruchu jego cząsteczek. Dla jednego mola takiego gazu jest ona równa:
U = ![]()
NA = ½ikNAT = ½iRT
Jest zatem funkcją tylko temperatury bezwzględnej, do której jest wprost proporcjonalna.
Wychodząc z równania na ciśnienie gazu i wykorzystując zależności dotyczące energii kinetycznej cząsteczki gazu
p = ![]()
/ თ ၵ
pၵ = ![]()
pၵ = ![]()
WK
pၵ = ![]()
![]()
თ N
pၵ = ![]()
თ ![]()
kT თ N
pၵ = ![]()
თ N
pၵ = nRT
w wyniku prostych przekształceń dojść możemy do równania stanu gazu doskonałego.
Wyszukiwarka