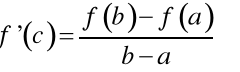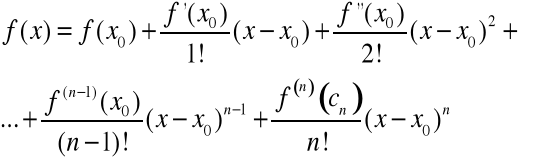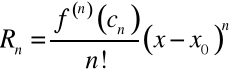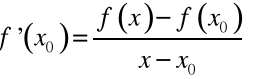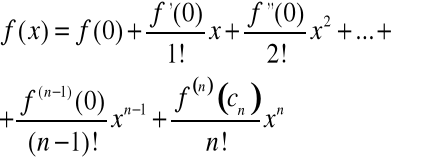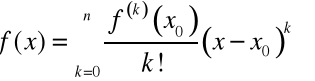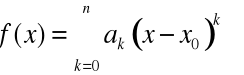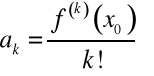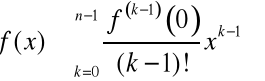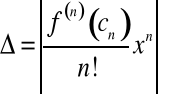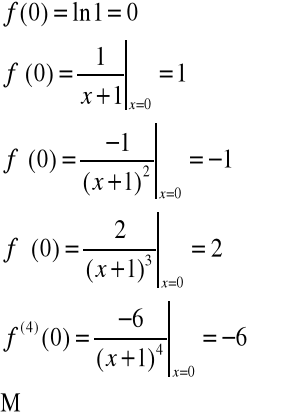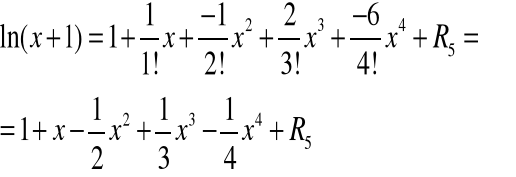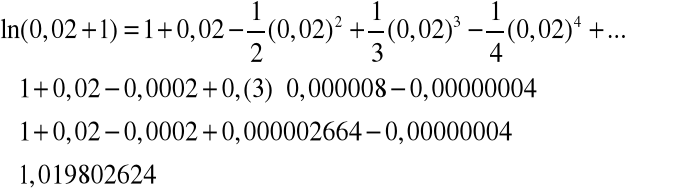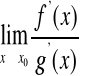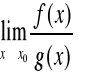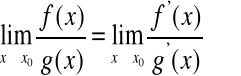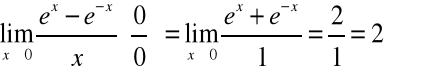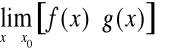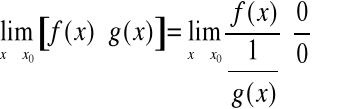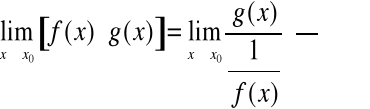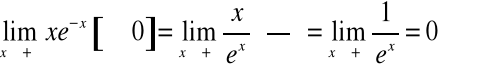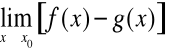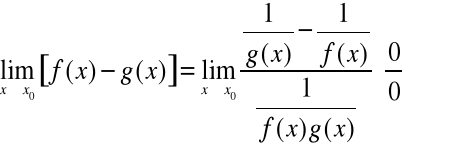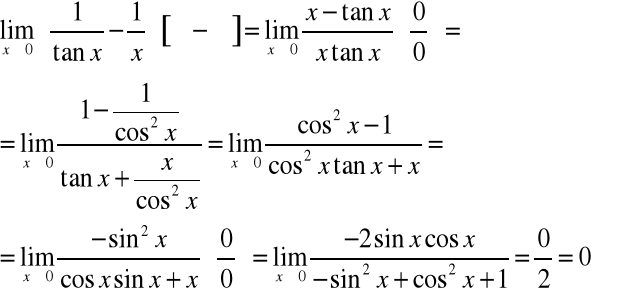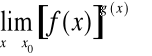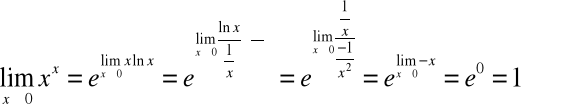RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ CZ.3
Twierdzenia o wartości średniej.
Poniższe trzy twierdzenia zwane są twierdzeniami o wartości średniej.
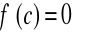
Twierdzenie 1. (ROLLE'A)
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]
[Author ID0: at Tue Aug 14 14:57:00 2001
] oraz [Author ID0: at Tue Aug 14 14:58:00 2001
][Author ID0: at Tue Aug 14 14:58:00 2001
]
[Author ID0: at Tue Aug 14 14:58:00 2001
], to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że
.
Twierdzenie 2. (CAUCHY'EGO )
Jeżeli funkcje 
i 
są ciągłe w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalne w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]
[Author ID0: at Tue Aug 14 14:57:00 2001
] to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że
.
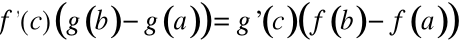
Twierdzenie 3. (LAGRANGE'A).
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]
[Author ID0: at Tue Aug 14 14:56:00 2001
]i różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]
[Author ID0: at Tue Aug 14 14:57:00 2001
], to istnieje punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że
.
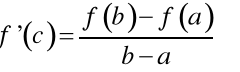
Szeregi Taylora i Maclaurina
Definicja 1.
Niech funkcja 
ma w punkcie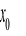 
pochodne dowolnego rzędu.
Szereg potęgowy
nazywamy szeregiem Taylora funkcji 
o środku w punkcie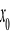 
.
Ostatni składnik sumy występującej w powyższym wzorze oznaczać będziemy jako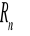 
i nazywać resztą w postaci Lagrange'a. Tak więc
Wniosek. Dla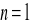 
otrzymujemy twierdzenie Lagrange'a.
Jeżeli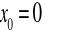 
, to szereg ten nazywamy szeregiem Maclaurina funkcji 
Twierdzenie 4. (o rozwijaniu funkcji w szereg Taylora).
Jeżeli:
funkcja
ma w otoczeniu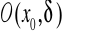
pochodne dowolnego rzędu,
dla każdego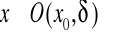
,
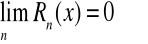
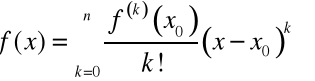
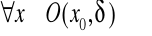
to
, 
.
Twierdzenie 5. (O jednoznaczności rozwinięcia funkcji w szereg potęgowy)
Jeżeli
, 
.
to
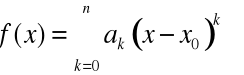
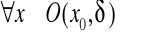
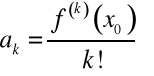
dla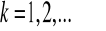 
.
Wzór Taylora oraz wynikający z niego wzór Maclaurina, o których była mowa wykorzystuje się do obliczania przybliżonych wartości funkcji.
Ze wzorów tych możemy otrzymać przybliżenia z mniejszym błędem niż wykorzystując różniczkę pierwszego rzędu.
Zauważmy, że pomijając resztę we wzorze np. Maclaurina, otrzymamy wzór przybliżony
,
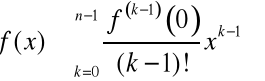
który możemy wykorzystać do obliczania wartości funkcji f.
Błąd bezwzględny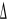 
, jaki popełniamy posługując się tym wzorem, jest równy wartości bezwzględnej
reszty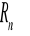 
, tj.
Przykłady
Napisać wzór Maclaurina dla funkcji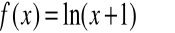
i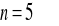
Policzmy:
Zapiszemy teraz wzór Maclaurina:
2. Oblicz korzystając z powyższego przybliżenia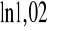 
.
Przypomnijmy, że licząc przybliżoną wartość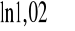 
za pomocą różniczki funkcji jednej zmiennej otrzymaliśmy mniej dokładny wynik 1,02.
Twierdzenie 6.
Niech 
, 
będą funkcjami różniczkowalnymi na przedziale I oraz niech 
. Jeżeli 
oraz 
, to 
.
Twierdzenie 7. (REGUŁA DE L'HOSPITALA)
Niech 
i 
będą funkcjami różniczkowalnymi w pewnym sąsiedztwie 
oraz
.
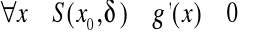
Jeżeli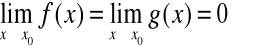 
lub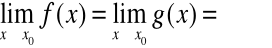 
oraz istnieje granica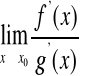 
(właściwa lub nie),
to istnieje również granica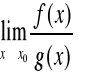 
przy czym
.
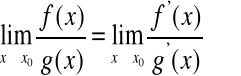
Uwaga. Twierdzenie odwrotne nie jest prawdziwe.
Z reguły de l'Hospitala możemy skorzystać w następujących przypadkach:
Przypadek 1.
Niech 
i 
lub niech 
i 
.
Obliczanie granicy poprzez formalne podstawienie wartości granicznych daje nam symbol nieoznaczony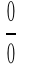 
lub odpowiednio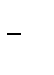 
.
W tym przypadku bezpośrednie (być może wielokrotne) zastosowanie reguły de l'Hospitala doprowadzi nas do rozwiązania.
Np.
.
Prz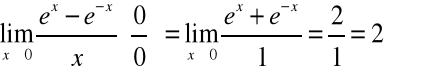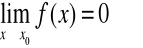ypadek 2.
Niech 
i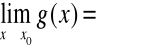 
.
Obliczając granicę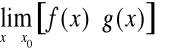 
poprzez formalne postawienie wartości granicznych otrzymamy symbol nieoznaczony
.
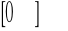
Aby wyznaczyć tę granicę zauważmy, że
lub
Np.
.
Przypadek 3.
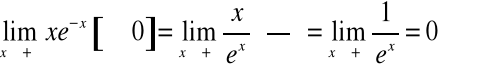
Niech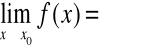 
i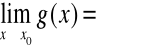 
.
Obliczając granicę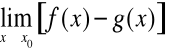 
poprzez formalne postawienie wartości granicznych otrzymamy symbol nieoznaczony
.
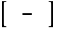
Zauważmy, że wówczas mamy:
Np.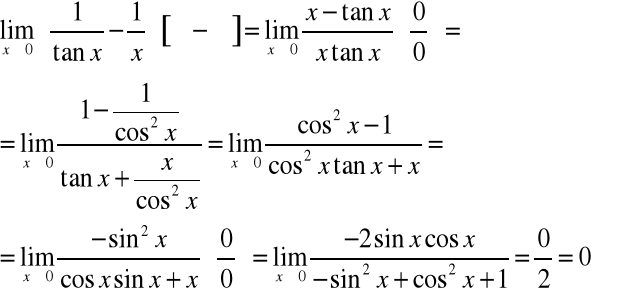 
Przypadek 4.
Niech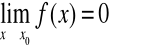 
i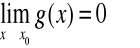 
.
Obliczając granicę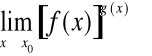 
poprzez formalne postawienie wartości granicznych otrzymamy symbol nieoznaczony
.
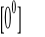
Podobnie gdy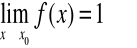 
i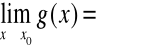 
obliczając
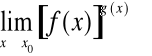
otrzymujemy inny symbol nieoznaczony
.
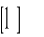
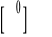
Również gdy 
i 
obliczając 
otrzymujemy inny symbol nieoznaczony
.
We wszystkich tych przypadkach 
, 
, 
obliczenie 
sprowadza się do obliczenia 
, co daje symbol 
.
Np.
Wyszukiwarka