
Andrzej Kądziołka 11.01.2006
Sprawozdanie z ćwiczenia nr 15.
Badanie rozkładu niepewności pomiarowych w pomiarach okresu wahań wahadła.
1. Zagadnienia do samodzielnego pracowania:
Niepewność standardowa u(x) wyraża się wzorem:

Wielkość ![]()
nazywa się odchyleniem standardowym wartości średniej. Przy założeniu, że wyniki kolejnych pomiarów podlegają rozkładowi normalnemu (Gaussa), prawdopodobieństwo znalezienia wartości oczekiwanej ![]()
w przedziale (xśr-u, xśr+u) wynosi ok. 67%. W przypadku, gdy rozkład wyników nie jest normalny nie znamy tego prawdopodobieństwa i poprzestajemy na podaniu wyniku w formie dwóch liczb: xśr i u.
Miarą rozproszenia wyników w serii pomiarowej jest tzw. odchylenie standardowe pojedynczego pomiaru sx (estymator odchylenia standardowego s) wyrażone wzorem:
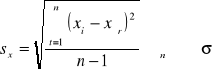
Jeżeli liczba pomiarów (n) dąży do nieskończoności, to wartość średnia (xśr) dąży do wartości oczekiwanej (![]()
), a odchylenie standardowe pojedynczego pomiaru sx dąży do odchylenia standardowego ![]()
rozkładu normalnego. Gęstość prawdopodobieństwa rozkładu normalnego (Gaussa) wyraża się wzorem:

gdzie wartość oczekiwana ![]()
jest, dla tego rozkładu, również wartością najbardziej prawdopodobną, a ![]()
jest odchyleniem standardowym. Funkcja Gaussa ma kształt dzwonowy i jest symetryczna względem ![]()
. Całka tej funkcji (pole pod wykresem P(x)) liczona od x1 do x2 określa prawdopodobieństwo uzyskania wyników pomiaru w przedziale (x1, x2). I tak, prawdopodobieństwo uzyskania wyników
w przedziale ![]()
wynosi ok. 67%,
w przedziale ![]()
wynosi ok. 95%,
w przedziale ![]()
wynosi ok. 99,7%.
Wahadło matematyczne jest to wyidealizowane ciało o punktowej masie zawieszone na cienkiej, nierozciągliwej i nieważkiej nici.
l - długość nici
N - naprężenie
γ - kąt odchylenia nici od pionu
2. Wykonanie ćwiczenia:
1. Zmierzyć przy pomocy sekundomierza czas t pięciu wahnięć wahadła.
Pomiary powtórzyć 100 razy zachowując stałą wielkość wychylenia początkowego
ok.![]()
, co odpowiada wychyleniu kulki o ok. 7 cm od położenia równowagi.
2. Obliczyć wartość średnią pomiarów![]()
.
3. Obliczyć odchylenie standardowe wartości średniej ![]()
.
4. Obliczyć odchylenie standardowe pojedynczego pomiaru ![]()
.
5. Narysować na papierze milimetrowym wykres funkcji Gaussa P(t) przyjmując, że wykonana ilość pomiarów pozwala założyć równości: ![]()
oraz ![]()
.
6. Obliczyć ilość k wyników pomiarów przypadających na określone przedziały o wielkości ![]()
równej np. 0.1s rozłożone symetrycznie względem przedziału (tśr -0.05s, tśr +0.05s).
7. Wyznaczyć prawdopodobieństwo p(![]()
) otrzymania wyniku pomiaru w danym przedziale obliczając pole pod krzywą Gaussa P(t) w tym przedziale. Wyniki zapisać w tabeli 2.
8. Wykonać wykres (histogram) przedstawiający w postaci kolumn w poszczególnych przedziałach wyniki zawarte w tabeli 2.
9. Obliczyć okres wahań T wahadła i niepewność standardową okresu. Obliczyć niepewność standardową względną.
10. Obliczyć okres wahań wahadła ![]()
traktując je jako wahadło matematyczne.
Długość wahadła zmierzona do środka kulki wynosi (132.0 ± 0.5)cm.
Obliczyć metodą różniczki zupełnej niepewność maksymalną ![]()
.
11. Przedstawić własne uwagi i wnioski dotyczące otrzymanych wyników.
3. Obliczenia i rachunek błędów:
Wszelkie obliczenia oraz wykresy zostały wykonane w programie Microsoft Excel. Znajdują się w pliku „Obliczenia - sprawozdanie nr 15” na dołączonej dyskietce.
Obliczam wartość średnią pomiarów:
![]()
![]()
Obliczam odchylenie standardowe wartości średniej:
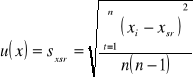
![]()
Obliczam odchylenie standardowe pojedynczego pomiaru:

![]()
Wykres funkcji Gaussa (wykonany w programie Microsoft Excel):
Ilość k wyników przypadających na określony przedział:
|
k |
k/100 |
tśr-0,45s,tśr -0,35s |
1 |
0,01 |
tśr-0,35s,tśr -0,25s |
4 |
0,04 |
tśr-0,25s,tśr -0,15s |
14 |
0,14 |
tśr-0,15s,tśr -0,5s |
29 |
0,29 |
tśr-0,05s,tśr+0,05s |
32 |
0,32 |
tśr+0,05s,tśr+0,15s |
13 |
0,13 |
tśr+0,15s,tśr+0,25s |
7 |
0,07 |
Histogram przedstawiający w postaci kolumn wyniki zawarte w tabeli znajdującej się powyżej (wykonany w programie Microsoft Excel):
Obliczam średni okres drgań wahadła:
![]()
Obliczam niepewność standardową okresu:

![]()
Okres wahań wahadła jako wahadło matematyczne:
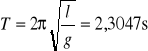
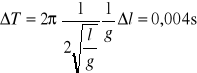
![]()
4. Wnioski:
Ćwiczenie to miało na celu zbadanie rozkładu niepewności pomiarowych. Jego przeprowadzenie było dosyć żmudne gdyż należało 100 razy zmierzyć czas 5 wahnięć wahadła. Można zauważyć, że większość wyników pomiarów zlokalizowała się w przedziale od 11,3 do 11,4s. Stanowią one 51% wszystkich zmierzonych czasów wahnięć wahadła. Natomiast średnia: 11,354s wskazuje na to, że pozostałe pomiary zlokalizowały się względnie symetrycznie po obu stronach tego przedziału, po czym możemy wnioskować, iż ćwiczenie zostało przeprowadzone poprawnie. Wskazuje na to również narysowana funkcja Gaussa oraz histogram.