
III inf. Sekcja I |
Wykonawcy : Patrycja Kuć Arkadiusz Krzystała
|
Ocena |
||
Ćwiczenie nr |
Temat: ZDEJMOWANIE CHARAKTERYSTYK CZĘSTOTLIWOŚCIOWYCH PRZEBIEGÓW ODKSZTAŁCONYCH |
Data wykonania: 14.01.99. |
Data oddania: 25.01.99. |
|
I. OPIS ĆWICZENIA:
Celem ćwiczenia jest wykonanie pomiarów zawartości harmonicznych i ich amplitud dla napięcia prostokątnego i sinusoidalnego oraz pomiar wartości skutecznej i współczynnika zniekształceń napięcia odkształconego oraz zawartości harmonicznych napięcia sinusoidalnego i odkształconego.
II. OPIS UKŁADU POMIAROWEGO:
Ćwiczenie wykonujemy po podłączeniu następujących układów pomiarowych:
1. Pomiar amplitud harmonicznych:

Dzielnik napięcia jest potrzebny do obniżenia wartości napięcia wejściowego na woltomierzu selektywnym, który ma ograniczenie napięcia do 100 [mV].
2. Pomiar zniekształceń nieliniowych:
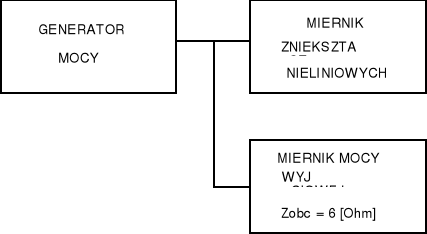
III. TABELE POMIAROWE
dla napięcia prostokątnego
Numer harmonicznej |
F [Hz] |
U [mV] |
1 |
20 |
52 |
2 |
40 |
1.9 |
3 |
60 |
18 |
4 |
80 |
2 |
5 |
100 |
10.5 |
6 |
120 |
1.9 |
7 |
140 |
7 |
8 |
160 |
1.9 |
9 |
180 |
5.6 |
10 |
200 |
1.9 |
11 |
220 |
4.4 |
12 |
240 |
1.9 |
13 |
260 |
3.6 |
dla napięcia sinusoidalnego
Numer harmonicznej |
F [Hz] |
U [mV] |
1 |
20 |
80 |
2 |
40 |
0.7 |
3 |
60 |
0.4 |
4 |
80 |
100 |
5 |
100 |
300 |
6 |
120 |
240 |
7 |
140 |
190 |
8 |
160 |
150 |
9 |
180 |
130 |
10 |
200 |
120 |
11 |
220 |
110 |
12 |
240 |
100 |
13 |
260 |
100 |
OBLICZENIA
Do obliczenia wartości skutecznej napięcia odkształconego oraz współczynnika zniekształceń harmonicznych posłużyliśmy się następującymi wzorami:
wartość skuteczna napięcia odkształconego
dla n=13
współczynnik zniekształceń harmonicznych
dla n=13
błąd wartości amplitudy napięcia odkształconego
δ Uodk = ((Uodkpom - Uodkobl ) / Uodkobl ) * 100 %
Wyliczony błąd wynosi:
dla sygnału sinusoidalnego 0.27 %
dla sygnału prostokątnego 8.41 %
Wartości napięć kolejnych harmonicznych w naszym sprawozdaniu wyznaczyliśmy dla napięcia o przebiegu prostokątnym. Sygnał z generatora możemy przedstawić w następujący sposób:
Opisującą ten sygnał funkcję
Funkcję g(t) możemy rozwinąć w szereg Fouriera według wzoru:
gdzie: f=1/T - częstotliwość podstawowa
an, bn - amplitudami n-tych harmonicznych
Dzieląc przedział całkowania na dwa podprzedziały (0,˝T) i (˝T,T) otrzymujemy po przeliczeniu następujące wartości:
Stąd otrzymujemy następujący wzór na obliczanie wartości napięć kolejnych harmonicznych:
Wykres.
Na wykresie przedstawiliśmy widmo Fouriera oraz gęstość widmową mocy dla sygnału prostokątnego. Zależność między i - tą harmoniczną gęstości widmowej mocy G(ω) a widmem Fouriera F(ω) przedstawia równanie:
Wnioski.
Jednym słowem ta labora była w dupe jerza kopanego łatwa , jestem wręcz rozczarowany poziomem kadry naukowej który jest co najmniej bordzo niski. Moim skromnyn zdaniem pownni oni uczyć budowy wentylka w przedszkolu. Dlatego z całym szacunkiem pierdolę tę budę.
Dla sygnału trójkątnego współczynnik zniekształceń maleje dla zadanej częstotliwości wraz ze wzrostem napięcia podawanego z generatora.
Przy pomiarze miernikiem selektywnym wartości poszczególnych harmonicznych sygnału o przebiegu prostokątnym został popełniony dość duży błąd, gdyż wartości teoretyczne dla parzystych harmoniczych powinny być zerowe. Wyliczona amplituda napięcia z generatora pokrywa się z wartością zmierzoną dla sygnałów sinusoidalnego i prostokątnego (wyliczony błąd jest niewielki wynika on z uwzględnienia niewielkiej liczby uwzględnionych harmonicznych). Zaobserwowana różnica dla sygnału trójkątnego (błąd 47 %) może wynikać stąd, że miernik selektywny nie mierzył napięcia dla ściśle określonej wartości częstotliwości f, lecz dla pewnego przedziału częstotliwości (f-Δf, f+Δf) /Δf jest tutaj pewną wartością charakterystyczną dla miernika /. Z tego względu miernik ten mógł rejestrować napięcia składowych harmonicznych zakłóceń, czyli pochodne innej częstotliwości f. Błąd ten też może wynikać ze sposobu przetwarzania wejściowego napięcia w mierniku.
Na wykresie widma Fouriera widać, że prążki poszczególnych nieparzystych harmonicznych maleją wraz ze wzrostem harmonicznych. Harmoniczne parzyste posiadają tutaj stałą wartość. Wartość ta jest różna od zera. Jest to najprawdopodobniej spowodowane błędami opisanymi powyżej. Drugi wykres przedstawia gęstość widmową mocy. Z wykresu widać, że największą moc w sygnale niesie pierwsza harmoniczna. Pozostałe nieparzyste harmoniczne niosą już mniej mocy. Natomiast dla harmonicznych parzystych widmo mocy powinno wynosić zero.
1. Pomiar amplitud harmonicznych dla napięcia prostokątnego i sinusoidalnego:
Z generatora podajemy częstotliwość f=20 [Hz] dla napięcia prostokątnego i sinusoidalnego.
Na woltomierzu wskazującym wartość skuteczną napięcia wejściowego odczytujemy następujące wartości:
- Uwe skut. = 3.2 [mV] dla napięcia prostokątnego;
Wartość skuteczną napięcia wyznaczamy z zależności:
![]()
W celu wyliczenia wartości skutecznej napięcia korzystamy z podanej wcześniej zależności:
Podobnie, jak w przypadku napięcia prostokątnego wartość skuteczną napięcia wyznaczamy z zależności:
2. POMIAR ZNIEKSZTAŁCEŃ NIELINIOWYCH:
Miernik mocy wyjściowej stanowi stałe obciążenie o wartości zobc=6 [Ω]. Również napięcie wyjściowe jest stałe.
TABELA POMIAROWA:
Lp. |
f [Hz] |
h [%] |
1 2 3 4 5 |
20 300 3000 7000 10000 |
0.3 0.24 0.17 0.17 0.18 |
WNIOSKI:
Celem ćwiczenia było zapoznanie się z budową i działaniem woltomierza selektywnego i miernika zniekształceń nieliniowych. Ponadto zbadaliśmy amplitudy kilku harmonicznych napięcia prostokątnego i trójkątnego, a następnie na ich podstawie obliczyliśmy wartość skuteczną napięcia korzystając ze wzoru:
Jak widać wyniki obliczone teoretycznie na podstawie pomiarów są nieco różne od wartości pomiaru przeprowadzonego przy pomocy miernika mierzącego napięcie skuteczne, przy czym różnica ta jest zdecydowanie większa w przypadku napięcia trójkątnego.
W drugiej części ćwiczenia dokonaliśmy pomiaru wartości zniekształceń nieliniowych oraz sporządziliśmy na ich podstawie charakterystykę h=f(częstotliwość f). Kształt tej charakterystyki jest zbliżony do wykładniczego, lecz ostatni pomiar jest większy, a nie mniejszy od wcześniejszych, co może być spowodowane złą kalibracją miernika lub innymi czynnikami zewnętrznymi mającymi wpływ na wartość tych pomiarów.
UU0
t
˝T T