Ćwiczenie 13

Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego

Wstęp:

Przyspieszeniem ziemskim nazywamy przyspieszenie swobodnego spadku ciał pod wpływem ich ciężaru Q. Zgodnie z II zasadą dynamiki:

(1)

gdzie: g - przyspieszenie ziemskie,

m - masa ciała.

Przyspieszenie ziemskie zmienia się w niewielkim zakresie w różnych punktach powierzchni Ziemi ze względu na zmienność ciężaru. Ciężar jest wypadkową skierowaną do środka Ziemi siły grawitacji oraz odśrodkowej siły bezwładności spowodowanej ruchem obrotowym Ziemi wokół jej osi:

(2)

Wartość siły bezwładności oraz jej kierunek względem kierunku siły grawitacji są zależne od szerokości geograficznej. Z tego powodu ciężar ciała jest wielkością zmienną zależną od miejsca na Ziemi, w którym ciało się znajduje.

Rys.1.

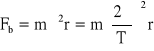
(3)

gdzie: ω - prędkość kątowa ruchu obrotowego Ziemi,

T - okres obiegu Ziemi wokół jej osi,

r - promień okręgu po którym porusza się ciało.

Na biegunach siła odśrodkowa nie występuje, dlatego ciężar przyjmuje tam największą wartość równą sile grawitacji działającej na ciało. Na równiku siła odśrodkowa ma ten sam kierunek, co siła grawitacji, a jej zwrot jest przeciwny. Ciężar jest najmniejszy. Drugim czynnikiem wpływającym na zmienność ciężaru jest spłaszczenie powierzchni Ziemi na biegunach. Kształt Ziemi jest zbliżony do kształtu spłaszczonej elipsoidy obrotowej. Jej krótsza półoś przechodząca przez biegun ma długość R_B = 6356,91 km, natomiast półoś równikowa R_R = 6378,79 km. Fakt ten zwiększa jeszcze bardziej różnicę pomiędzy ciężarem biegunowym i równikowym.α

Pomiary przyspieszenia ziemskiego na różnych szerokościach geograficznych pozwoliły na sformułowanie następującej zależności:

(4)

gdzie: α - szerokość geograficzna.

Najmniejsza i największa wartość przyspieszenia g wynosi odpowiednio:

Innym czynnikiem wpływającym na miejscowe zróżnicowanie ciężaru jest zmienna gęstość Ziemi. W częściach Ziemi zawierających złoża mineralne, których gęstość różni się od jej średniej gęstości, obserwuje się wyraźne lokalne zmiany wartości przyspieszenia ziemskiego. Fakt ten jest wykorzystywany w badaniach geologicznych skorupy ziemskiej.

W danym miejscu powierzchni Ziemi przyspieszenia spadku swobodnego wszystkich ciał jest oczywiście takie samo. Gdyby zaniedbać ruch obrotowy Ziemi i zmienność jej promienia wówczas można przyjąć, że:

(5)

czyli:

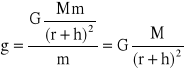
(6)

gdzie: G - stała grawitacji,

R - średni promień Ziemi,

h - wysokość ponad powierzchnią Ziemi,

M - masa Ziemi

Przyspieszenie ziemskie zależy więc od wysokości ponad powierzchnią Ziemi. Na wysokości 300 km zmniejsza się o około 1 m/s. Przy małych wysokościach dochodzących do kilku kilometrów nad powierzchnią Ziemi, przyspieszenie ziemskie można uważać z bardzo dobrą dokładnością za stałe

Przyrządy:

Wahadło rewersyjne, stoper, przymiar z podziałką milimetrową

Wahadłem rewersyjnym (odwracalnym) nazywamy bryłę sztywną, która zawieszona kolejno na dwóch osiach równoległych leżących po przeciwnych stronach jej środka ciężkości w nierównych od niego odległościach, ma taki sam okres drgań.

Okres swobodnych drgań dowolnego wahadła fizycznego wynosi:

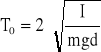
(7)

gdzie: l - moment bezwładności wahadła względem osi zawieszenia równoległej do osi O lecz

przechodzącej przez środek ciężkości wahadła,

m - masa wahadła

d - odległość środka ciężkości S wahadła od osi obrotów.

Powyższe równanie jest słuszne dla małych wychyleń wahadła z położenia równowagi (
)

Zgodnie z twierdzeniem Steinera moment bezwładności:

(8)

gdzie: l - moment bezwładności wahadła względem osi równoległej do osi O lecz przechodzącej

przez środek ciężkości wahadła.

Na podstawie równań (7) i (8) okres swobodnych drgań można zapisać zgodnie ze wzorem:

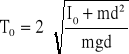
(9)

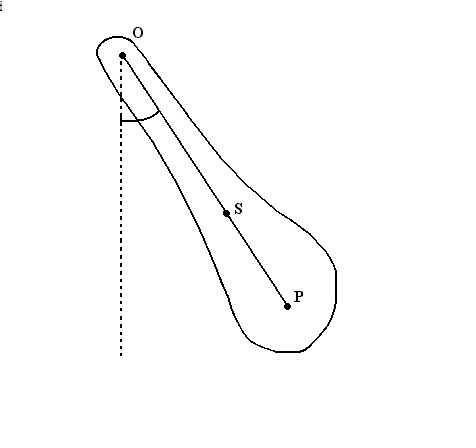
Istnieje inna oś P leżąca na linii OS (rys.2), po przeciwnej stronie środka ciężkości o własności takiej, że okres drgań wahadła wokół tej osi jest taki sam ja dla osi O. Zgodnie z oznaczeniami na rysunku:

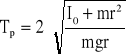
(10)

Porównując równania (9) i (10) wynika, że równość okresów ma miejsce, gdy:

(11)

czyli:

(12) rys.2.

(13)

(14)

Ostatnie równanie (14) określa odległość środka ciężkości wahadła od osi P.

Korzystając z równania (13), w którym moment bezwładności wahadła wyrażony jest przez odległość r, okres drgań wahadła można przedstawić w inny sposób. Podstawiając (13) do równań (9) i (10) otrzymujemy:

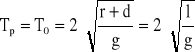
(15)

gdzie: l - odległość między osiami O i P, dla których okres drgań wahadła jest taki sam.

Wzór (15) opisuje okres drgań wahadła matematycznego o długości l. Długość tą nazywamy długością zredukowaną wahadła. Jeśli dla danego wahadła fizycznego wyznaczona zostanie odległość l między osiami zawieszenia o tym samym okresie drgań oraz zmierzona zostanie wartość tego okresu T, to wówczas możliwe jest wyznaczenie przyspieszenia ziemskiego zgodnie z przekształconym wzorem (15) do postaci:

(16)

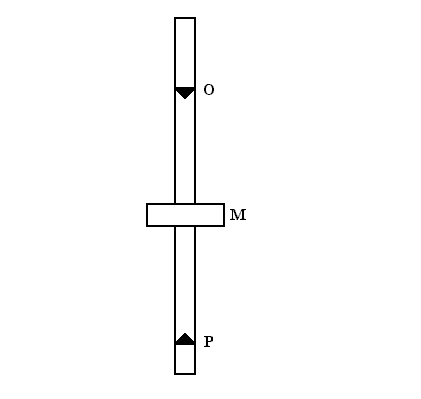
Wahadło rewersyjne zastosowane w ćwiczeniu ma postać stalowej sztaby, na której znajduje się obciążnik M w kształcie dysku (rysunek obok). Obciążnik można przesuwać w odczytywać jego położenie na skali naniesionej na sztabę. Dwa pryzmaty przymocowane prostopadle do sztaby pełnią rolę osi zawieszenia O i P. Odległość osi jest zatem w doświadczeniu ustalona. Przesuwanie obciążnika wzdłuż sztaby powoduje zmianę położenia środka ciężkości wahadła względem osi. W trakcie przeprowadzania doświadczenia znajdowane jest takie położenie obciążnika, przy którym okresy wahań wahadła względem obu osi staja się takie same. Wtedy odległość między osiami staje się długością zredukowaną wahadła.

Przebieg ćwiczenia:

1. Zmierzyć odległość pomiędzy osiami wahadła l = O₁O₂ i oszacować błąd tego pomiaru Δl.

2. Zawiesić wahadło na ostrzu O₁ i przesunąć masę M na środek pręta.

3. Wykonać serię m=10 pomiarów czasu t dziesięciu drgań (n=10) bez zmiany położenia masy M. Wyniki zanotować w tab.1 i na ich podstawie obliczyć wartość średnią t i średni błąd kwadratowy S_t pojedynczego pomiaru skorygowany przez odpowiedni współczynnik Studenta-Fishera:

S_t = S'_tt_α,m

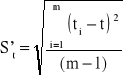
Tab.1.

t1 [s]	t2 [s]	t3 [s]	....	t9 [s]	t10 [s]	t [s]	S't [s]	tα,m	St [s]

4. Przesunąć masę M do ostrza swobodnego O₂ i wykonać serię pojedynczych pomiarów czasów t' dziesięciu drgań przesuwając masę M w kierunku osi wahadła, co 5 cm (kolejne położenia k_n masy M zaznaczone są na pręcie liniami).

5. Obrócić wahadło i zawiesić je na drugiej osi, po czym powtórzyć pomiary jak w punkcie 4 mierząc czasy t''.

6. Wyniki pomiarów zanotować w tab.2 i na ich podstawie sporządzić wykresy t'=f(k_n) i t''=f(k_n) w tym samym układzie współrzędnych. Na każdy punkt pomiarowy nanieść "słupek" błędu o wysokości 2S_t i narysować gładkie krzywe zmian czasów t' =f(k_n) i t''=f(k_n).

7. Z wykresu odczytać współrzędne t'₀ i t''₀ punktów przecięcia się krzywych t'(k_n) i t''(k_n).

8. Obliczyć średni czas dziesięciu drgań t₀ = (t'₀ + t''₀)/2 i oszacować błąd Δt₀ wg wzoru :

gdzie: Δt'₀ = |t'₀ - t''₀|/2

9. Obliczyć okres drgań wahadła T₀.

10. Obliczyć przyspieszenie ziemskie g i błąd bezwzględny Δg ze wzorów:

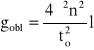
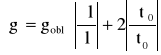
11. Wyniki obliczeń zamieścić w tab.3.

Tab.2.

kn [cm]

t' [s]

t'' [s]

Tab.3.

t'0= [s]	t''0= [s]	t0= [s]	Δt'0= [s]	Δt0= [s]
T0= [s]	l= [m]	Δl= [m]	g= [m/s^2]	Δg= [m/s^2]

Wymagania

• Wahadło fizyczne (ruch harmoniczny prosty, moment siły, wyprowadzenie wzoru na okres drgań wahadła fizycznego i wahadła rewersyjnego).

• Charakterystyka pola grawitacyjnego (natężenie i potencjał pola):

• punktu materialnego

• kuli o promieniu R i gęstości ρ (uzasadnienie z zastosowaniem prawa Gaussa).

• Wpływ kształtu i ruchu obrotowego Ziemi na przyspieszenie ziemskie g.

---