Wstęp do Analizy Matematycznej - 1 kolokwium - studia zaoczne

Zad.1 Sprawdzić, czy następujące schematy zdań są tautologiami:

a) [(p
q) ^ (p
q)]
(q
p) ;

b) p
[(~q ^ q)
r ] ;

c) [( p
q ) ^ p]
q ;

d) [(p ^ q)
r]
(p
r) ^ (q
r) ;

e) (p
q)
[(p ^ q)
p] ;

f) [~ (p
q)]
(p ^ ~ q) ;

g) [(p ^ q)
p]
q;

h) [~ (p ^ q)]
[~ p
~ q] ;

i) (p ^ q)
(p
q) ;

j) [(p
q)
p]
q.

Zad.2 Zapisz używając kwantyfikatorów następujące zdania:

a) Każda liczba naturalna jest liczbą całkowitą.

b) Iloraz liczb naturalnych nie musi być liczbą naturalną.

c) Iloraz liczb naturalnych może być liczbą naturalną.

d) Dla każdej liczby wymiernej można dobrać liczbę całkowitą taką, że ich iloczyn jest liczbą całkowitą.

e) Żadna liczba rzeczywista nie jest rozwiązaniem równania x² + 2 = 0.

f) Istnieje ciąg rosnący.

g) Dla każdej liczby całkowitej x iloczyn f(x)f(y) jest dodatni, o ile y jest liczbą ujemną.

Zad.3 Rozwiąż równania i nierówności

a)

b)

c)

d)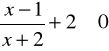

e)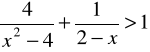

f)

g)

h)

i)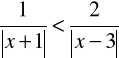

j)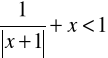

k)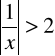

l)

Zad. 4 Narysuj zbiory:

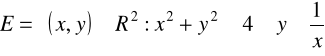
Zad. 5 Wyznacz i narysuj zbiory
,
,
,
,
,
, gdy: a)
,

b)
,

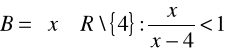
c)
,

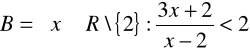
Zad.6 Narysuj iloczyn kartezjański
następujących zbiorów:

a)
,

b)
,

c)
,

d)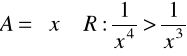
,

e)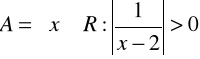
,

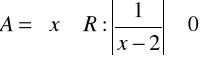
f)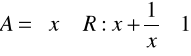
,

Zad.7 Naszkicuj wykres funkcji:

a)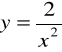

b)

c)

d)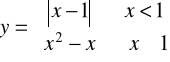

e)

---