WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM FIZYCZNE

Grupa szkoleniowa : E03D8 Podgr. : .................................

(stopień i nazwisko

prowadzącego ćwiczenia)

Budziński Dawid

..........................................

(nazwisko i imię słuchacza)

........................ .......................

ocena przygot. ocena końcowa

do ćwiczenia

SPRAWOZDANIE

Z

PRACY LABORATORYJNEJ NR 36

WYZNACZENIE MOMENTU BEZWŁADNOŚCI BRYŁY Z WYKORZYSTANIEM MASZYNY ATWOODA

(temat pracy)

1. Wstęp teoretyczny

Maszyna Atwooda służy do doświadczalnego sprawdzania praw kinematyki i dynamiki (I i II zasada Newtona). W najprostszym wykonaniu składa się z bloczka K umieszczonego w górnej części pionowego pręta ze skalą S. Przez bloczek przechodzi cienka i mocna nić z zawieszonymi na końcach równoważnymi ciężarkami M g (M - masa ciężarka, g - przyśpieszenie ziemskie). Dodatkowo obciążenie k m_o g (k - ilość jednakowych blaszek o masie m_o) jednego z ciężarków wprowadza układ ciężarek - nić - bloczek w ruch jednostajnie przyśpieszony.

K

A

S

B

W maszynie Atwooda mamy do czynienia z dwoma rodzajami ruchu: prostoliniowym jednostajnie zmiennym ciężarków i obrotowym jednostajnie zmiennym bloczka, przez który przełożona jest nić łącząca ciężarki.

W ćwiczeniu będziemy się zajmować wyznaczeniem momentu bezwładności ciała względem osi obrotu. Zależy więc od wyboru osi obrotu i rozłożenia masy względem niej oraz kształtu ciała:

Moment bezwładności rury cylindrycznej (albo pierścienia) o masie m, wewnętrznym promieniu R₁ i zewnętrznym R₂ wynosi:

Przyspieszenie obliczamy ze wzoru:

Moment bezwładności bloczka K wyznaczmy ze wzoru:

Gdzie:

k -ilość jednakowych blaszek;

m_o - masa jednej blaszki;

M - masa ciężarka;

a - przyśpieszenie;

r - promień bloczka.

Umieszczając na osi bloczka dodatkowe ciało (w ćwiczeniu metalowy pierścień), korzystając z wyprowadzonych wielkości, można wyznaczyć moment bezwładności J_c, będący sumą momentu bezwładności bloczka J_u i dołożonego ciała J_b. Szukana bezwładność jest więc równa różnicy:

J_b = J_c - J_u.

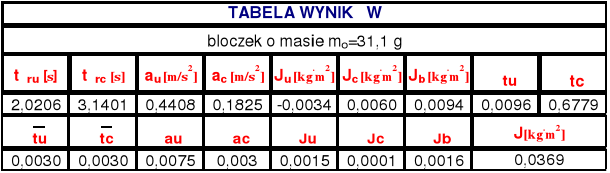
2. Wyniki pomiarów

Dla mo=31,1 g
LP	Bloczek bez obciążenia	Bloczek z obciążenia
		t [s]	t [s]
1	2,013	3,128
2	2,018	3,187
3	2,019	3,084
4	2,040	3,067
5	2,043	3,078
6	2,018	3,134
7	2,011	3,195
8	2,006	3,191
9	2,016	3,186
10	2,022	3,151

3. Wyniki obliczeń:

1. Obliczenia dla nie obciążonego bloczka przy m_o=31,1 g:

1. 
   Obliczam czas średni t_u:

2. Obliczam przyspieszenie:

S = 900 mm = 900^.10^-3m = 0,9 m

t_u=2,0206 s

3. Obliczam moment bezwładności:

k=1

m_o=31,1g=31,1^.10^-3 kg = 0,0311 kg

M= 507 g = 507^.10^-3 kg = 0,507 kg

r= 98 mm = 98^.10^-3 m = 0,098 m

2. Obliczenia dla obciążonego bloczka przy m_o=31,1 g:

1. 
   Obliczam czas średni t_u:

2. Obliczam przyspieszenie:

S = 900 mm = 900^.10^-3m = 0,9 m

t_c=3,1401 s

4. Obliczam moment bezwładności:

k=1

m_o=31,1g=31,1^.10^-3 kg = 0,0311 kg

M= 507 g = 507^.10^-3 kg = 0,507 kg

r= 98 mm = 98^.10^-3 m = 0,098 m

Obliczam moment bezwładności dla dołożonego ciała:

Przy J_c= 0,00602 [kg m²]

J_u=-0,0034 [kg m²]

J_b=0,00602-(-0,0034)= 0,00942 [kg m²]

Obliczenie błędów.

1. Obliczenia dla nie obciążonego bloczka przy m_o=31,1 g:

1. 
   Obliczam odchylenie standardowe δ_tu:

2. Obliczam optymalny średni błąd kwadratowy:

N=10

6. 
   Obliczam średni błąd kwadratowy δ_au:

δ=15 mm = 15^.10^-3 m =0,015 m

S=0,9 m

t_u=2,0206 s

7. Obliczam średni błąd kwadratowy δ_Ju:

Błędy δ obliczam ze wzoru:

δ_x = x/x

g=9,81 [kg/m²]

r=0,098 [m] δ_r=0,01

m_o=31,1 [g]=0,0311 [kg] δ_mo=0,0032

M=507 [g]= 0,507 [kg] δ_M=0,002

a_u=0,4408 [m/s²] δ_au=0,0075

2. Obliczenia dla obciążonego bloczka przy m_o=31,1 g:

3. 
   Obliczam odchylenie standardowe δ_tc:

4. Obliczam optymalny średni błąd kwadratowy:

N=10

8. 
   Obliczam średni błąd kwadratowy δ_ac:

δ=15 mm = 15^.10^-3 m =0,015 m

S=0,9 m

t_c=3,1401s

9. Obliczam średni błąd kwadratowy δ_Jc:

Błędy δ obliczam ze wzoru:

δ_x = x/x

g=9,81 [kg/m²]

r=0,098 [m] δ_r=0,01

m_o=31,1 [g]=0,0311 [kg] δ_mo=0,0032

M=507 [g]= 0,507 [kg] δ_M=0,002

a_c=0,1825 [m/s²] δ_au=0,0075

Obliczam błąd δ_Jb:

δ_Jb δ_Jcδ_Ju

δ_Jc ,

δ_Ju ,

δ_Jb ,,,

• 
  Obliczam moment bezwładności pierścienia za pomocą wzoru:

R₁=100 [mm] = 0,100 [m]

R₂=164 [mm] = 0,164 [m]

m=2001 [g] =2,001 [kg]

4. Wnioski:

Celem ćwiczenia było wyznaczenie bezwładności bryły z wykorzystaniem maszyny ATWOODA. Wyniki jakie otrzymaliśmy nieznacznie się różnią od wartości obliczonej teoretycznie. A mianowicie moment bezwładności pierścienia obliczony na podstawie wzoru teoretycznego wynosi 0.009229 kg m². Zaś obliczony na podstawie dokonanych przez nas pomiarów zamyka się w przedziale od 0.0094 kg m² do 0.036 kg m². Drobne rozbieżności jakie występują pomiędzy wartością momentu bezwładności obliczoną teoretycznie i na podstawie dokonanych pomiarów, wynikają z błędów jakie niewątpliwie powstały podczas wykonywania pomiarów. A mianowicie błędy wynikające z niedokładnego odczytu z linijki, jej błędu, błędem jaki występował podczas pomiaru czasu, wpływem czynników zewnętrznych, błędami przypadkowymi, które popełniliśmy wykonując ćwiczenie. Jednak, że w obliczeniach pominięta została siła tarcia między bloczkiem, a nicią która miała niewątpliwy wpływ na otrzymane wyniki. Należy też zwrócić uwagę, na fakt pominięcia wyżej wspomnianej siły w obliczeniach teoretycznych. Dlatego wnioskuje, że dokonane przez nas pomiary nie są obarczone dużym błędem a różnica w obliczonym momencie bezwładności wynika z nieuwzględnienia tejże siły oraz wspomnianych wyżej błędów.

---
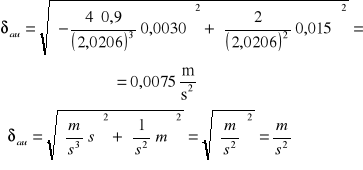
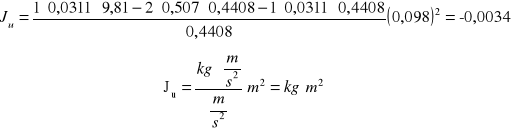
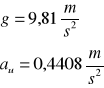
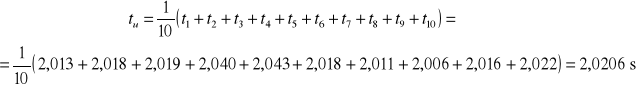
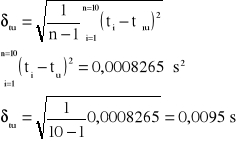
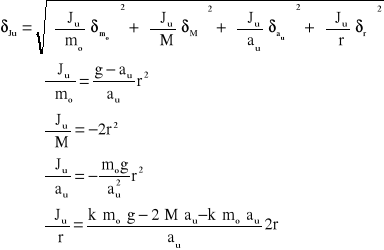
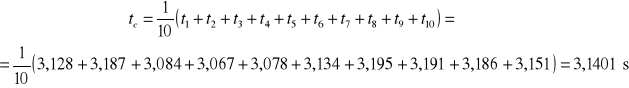
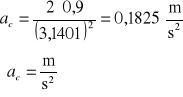
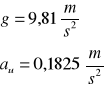
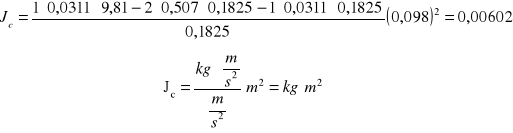
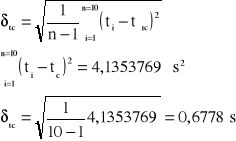
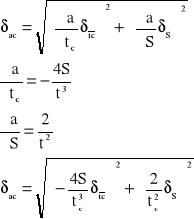
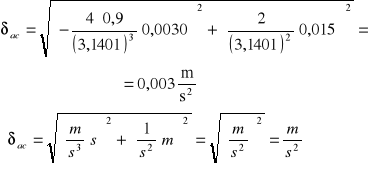
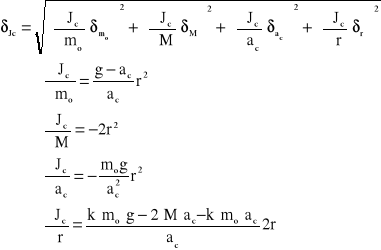