Sprawozdanie

Politechnika Śląska

Wydział MT

Kierunek MiBM

Ćwiczenie laboratoryjne z fizyki:

Wyznaczanie współczynnika załamania szkła dla pryzmatu. Badanie zależności kąta skręcenia płaszczyzny polaryzacji od stężenia wodnego roztworu cukru.

Grupa II sekcja VIII

Pior Płonka

Jacek Pańtak

1. Cześć teoretyczna

1.1. Współczynnik załamania światła

Przechodząc z jednego ośrodka do drugiego wiązka światła ulega załamaniu oraz pochłanianiu i rozpraszaniu. Jeśli światło przechodzi z ośrodka optycznie rzadszego do gęstrzego, to wiązka promieni zbliża się do prostej prostopadłej względem płaszczyzny rozgraniczającej dwa ośrodki. Przeciwnie zaś dzieje się jeśli promienie biegną z ośrodka gęstrzego do rzadszego liczbowo ujmuje to prawo Snelliusa
, gdzie n jest stałą i nosi nazwę współczynnika załamania ośrodka drugiego względem ośrodka pierwszego, zaś i . są kątami padania i załamania wiązki. Współczynnik n posiada ważny sęs fizyczny, mianowicie
, gdzie VI oznacza prędkość rozchodzenia się swiatła w ośrodku I, VII - w ośrodku II. Wynika to z teori falowej światła i z zasady Hyghensa. Prawo Snelliusa ilustruje rycina:

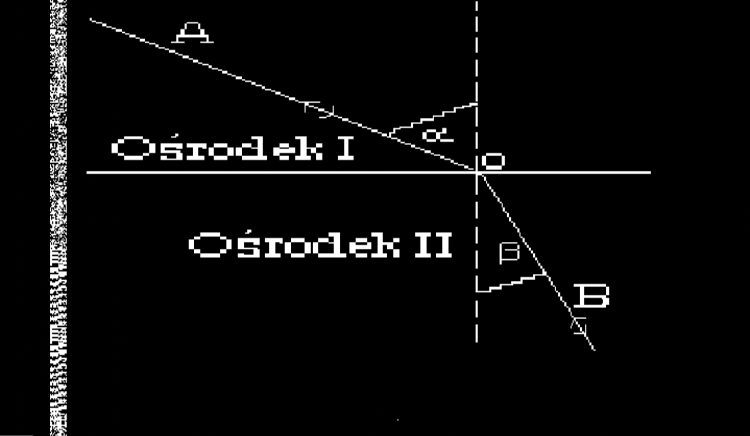
Pożytecznie będzie zauważyć, że jeśli światło poda wzdłuż prostej BO i wychodzi z ośrodka II to pójdzie dokładnie w kierunku prostej OA, jak to symbolizują strzałki narysowane w obu kierunkach. Jest to przejawem stosowanej w optyce geometrycznej ogólnej zasady odwracalności biegu promieni.

Jedna z metod pomiaru współczynnika załamania światła opiera się na zjawisku odchylenia biegu promieni przez pryzmat. Ciało, którego współczynnik załamania wyznaczamy, ma w tym przypadku kształt pryzmatu. Jeśli jest to ciało stałe, bryłę pryzmatyczną uzyskuje się przez odpowiednie szlifiowanie. W przypadku cieczy posługujemu się naczyniem pryzmatycznym o sciankach płasko-równoległych, do którego nalewamy badaną ciecz. Wyznaczanie kątów padanie a i załamania b promieni w przypadku pryzmatu nie byłoby łatwe i możemy go uniknąć przekształcając wzór Selliusa tak, aby uwzględnic w nim zamiast kątów a i b kąt łamiący pryzmatu oraz kąt minimalnego odchylenia . Kątem odchylenia promieni nazywamy kąt zawarty pomiędzy kierunkiem promiena padającego na pryzmat i wychodzącego z pryzmatu. Kąt ten ma wartość minimalną wtedy gdy wewnątrz pryzmatu promień biegnie prostopadle do dwusiecznej kąta łamiącego, wówczas kąt padania a równa się kątowi wyjścia promienia z pryzmatu a1.

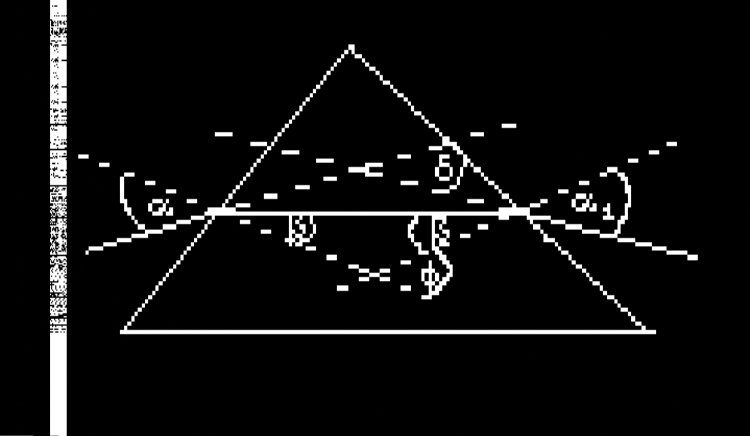
Wyprowadzenie wzoru:

. Dla przypadku najmniejszego odchylenia: otrzymujemy końcowy wzór: .

W powyższych wyliczeń wynika, że obliczenie współczynnika załamania światła dla pryzmatu w naszym przypadku sprowadza się do wyznaczenia kąta łamiącego pryzmatu i kąta minimalenego odchylenia. Oba pomiary dokonujemy za pomocą spektrometru, którego schemat został umieszczony niżej.

1.2. Kąt skręcenia płaszczyny polaryzacji w zależności od stężenia roztworu.

Światło spolaryzowane i zjawisko rotacji optycznej

W najczęstszym przypadku światło jest niespolaryzowane tzn. drgania wektorów natężenia pola elektrycznego i wektora natężenia pola magnetycznego odbywają się prostopadle do kierunku rozchodzenia się fali i do siebie nawzajem (parami), lecz we wszystkich możliwych płaszczyznach, w których ten kierunek leży. Można uznać w takim przypadku, że światło takie jest złożone z wielu fal o różnych płaszczyznach drgań. Gdy jakiś czynnik zmusi chaotyczne drgania do tego, by odbywały się w jednej płaszczyźnie lub jakiegoś innego obranego porządku, mówimy o polaryzacji światła. Najczęstszym przypadkiem jest polaryzacja liniowa, gdzie drgania już uporządkowane odbywają się ściśle w jednej płaszczyźnie.

W pewnych przypadkach płaszczyzna oscylacji wektora natężenia pola elektrycznego liniowo spolaryzowanego światła obraca się w miarę propagacji fali i obrót ten jest funkcją drogi przebywanej przez światło w danym ośrodku. Mówimy wówczas o zjawisku rotacji optycnej. W zależności od skręcenia płaszczyzny polaryzacji ośrodek może być prawo lub lewo skrętny. Ośrodki w których zjawisko rotacji optycznej zachodzi w watrunkach normalnych nazywamy ośrodkami optycznie aktywnymi. Aktywność optyczna danego ośrodka jest związana z ich budową wewnętrzną - np w wodnych roztworach cukru decydujące znaczenie ma ksztaut cząsteczki cukru. Wyjaśnienie teoretyczne zjawiska rotacji optycznej opiera się na fakcie, że nałożenie na siebie dwóch drgań spolaryzowanych kołowo o przeciwnych zwrotach prowadzi do drgań spolaryzowanych liniowo. Wychodząc z tego założenia przyjmuje się, że światło spolaryzowane liniowo w ośrodku aktywnym optycznie ulega rozkładowi na na dwie fale spolaryzowane kołowo: jedną lewoskrętnie i drugą prawoskrętnie oraz fale te propagują w danym ośrodku z różnymi prędkościami. Otrzymujemy następujący związek na zmianę płaszczyzny polaryzacji od przebytej drogi: , gdzie a to kąt skręcenia płaszczyzny polaryzacji, l to ługość danej fali w próżni, nl, np -względne współczynniki załamania fal spolaryzowanych lewo i prawo skrętnie w ośrodku optycznie aktywnym.

2. Opis metody pomiarowej

2.1. Pomiar kąta łamiącego pryzmatu

Aby zmierzyć kąt łamiący należy wyregulować spektrometr. Następnie badany pryzmat należy umieścic na stoliku spektrometru tak aby wiązka światła padała równolegle do dwusiecznej kąta łamiącego. Nasępnie należy zmierzyć kąty 1 i 2 odpowiadające promieniom odbitym od obu płaszczyzn badanych pryzmatu. Wartość kąta łamiącego obliczamy ze wzoru:
. Pomiarów dokonujemy za pomocą spektrometru, którego schemat zamieszczono niżej.

2.2.Pomiar kąta minimalnego odchylenia

Aby obliczyć kąt minimalnego odchylenia należy umieścić pryzmat na stoliku spektrometru, a następnie obracając lunetką odnajdujemy obraz szczeliny. Poruszając stolikiem obserwujemy zachowanie się obrazu. Prążek przesµwa się w polu widzenia. Zatrzymująe się i przesówa w przeciwnym kierunku. Naprowadzamy krzyż lunetki na obraz odpowiadający punktowi zwrotnemu. Sprawdzamy poprawność ustawienia minimalnego kąta.

Następnie ze wzoru:
, obliczamy kąt minimalnego odchylenia. Schemat układu został umieszczony wyżej.

2.3.Zależność kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu

Wszystkich pomiarów dokonano za pomocą polarymetru. Wykorzystuje on dużą wrażliwość oka ludzkiego na zmianę natężenia oświetlenia

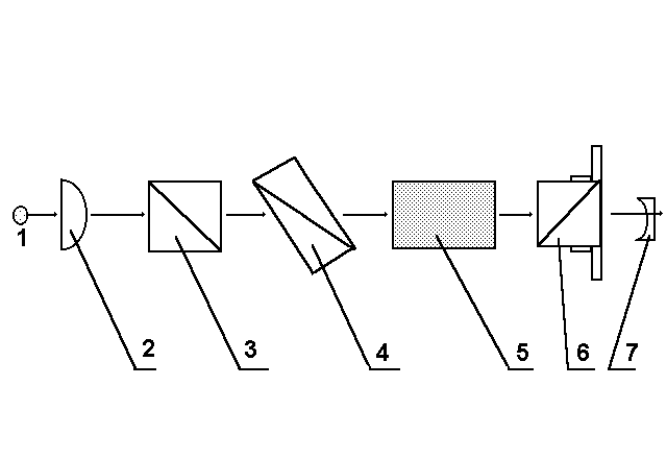
Schemat szczegółowy polarymetru

Ozn: 1 - źródło światła, 2 - soczewka, 3 - polaryzator, 4 - przyrząd półcieniowy, 5 - substancja aktywna optycznie, 6 - analizator, 7 - lunetka.

Światło liniowo spolaryzowane pada na przyrząd półcieniowy, który dzieli pole widzenia na części (zaciemnia płaszczyznę polaryzacji w jednej z nich). Za przyrządem półcieniowym płaszczyzny polaryzacji tworzą ze sobą niewielki kąt a. Dla uzyskania równego oświetlenia analizator ustawia się tak aby jego płaszczyzna polaryzacji dzieliła kąt a na dwie równe części. Po wprowadzeniu ciała optycznie czynnego płaszczyzna polaryzacji światła ulega skręceniu o taki sam kąt i w tym samym kierunku w obydwu częściach pola widzenia. Stąd aby uzyskać równość oświetlenia całego pola widzenia analizator należy skręcić o kąt równy kątowi skręcenia płaszczyzny polaryzacji.

3. Schematy układów i krótki opis przebiegu ćwiczenia

Ćwiczenie składało się z dwóch części. W pierwszej badaliśmy kąt łamiący (5 pomiarów) i minimalnego odchylenia pryzmatu (5 pomiarów), aby obliczyć współczynnik załamania światła dla pryzmatu. Pomiarów dokonano na układzie pokazanym na rysunku:

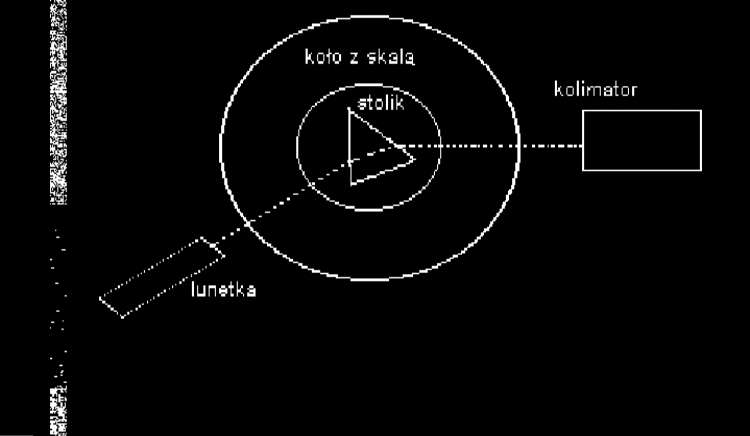
Schemat spektrometru

W drugiej części ćwiczenia badano zależność kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu. Pomiarów dokonano na poniższym układzie.

Schemat polarymetru

Ozn: 1 - źródło światła, 2 - substancja optycznie aktywna, 3 - polarymetr.

Układ stanowiło źródło światła (lampa sodowa) i polarymetr. W czasie ćwiczenia wymieniano kuwetę, umieszczaną na czas pomiaru wewnątrz polarymetru. Najpierw kuweta była wypełniona wodą , a następnie wodnymi roztworami sacharozy (w tym o stężeniu X, które mamy obliczyć). Pomiary kąta skręcenia analizatora polarymetru dla danego stężenia powtarzano trzykrotnie. Ogółem wykonano 16 pomiarów.

4.1. Obliczenia i rachunek błędów

4.1.1. Współczynnik załamania światła dla pryzmatu

4.1.1.1 Kąt łamiący pryzmatu

Obliczamy go według wzoru:
. Wyniki jakie otrzymano to:

lp.	1[]	2[]	[]
1
2
3
4
5
śr.

4.1.1.2 Kąt minimalnego odchylenia

Obliczamy go według wzoru:
. gdzie e0= .......[]. Wyniki jakie otrzymano to:

lp.	e[]	[]
1
2
3
4
5
śr.

4.1.1.3 Współczynnik załamania pryzmatu

Obliczamy go według wzoru: . Wyniki jakie otrzymano to:

...............................................................................................................................

Błędy wyniu otrzymanego wpółczynnika załamania światła obliczono metodą różniczki zupełnej. przekształcając wzór główny na . otrzymujemy:

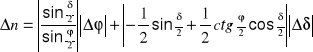
Błędy pomiaru wynoszą: Df=...... [] oraz Dd=...... []. Podstawiając do wzoru otrzymujemy Dn=............

4.1.2. Zależność kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu

Obliczono średnią arytmetyczną każdej serii pomiarów kąta skręcenia płaszczyzny polaryzacji przy danym stężeniu roztworu. Następnie według wzoru: aoi=ai-ao obliczono kąt skręcenia płaszczyzny polaryzacji względem wody. Otrzymano następujące wartości:

stężenie [%]	a - Kąt skręcenia [°]	ai - ao [°]
woda - 0		-
2
4
6
8
X

Posługując się metodą regresji liniowej obliczono współczynniki prostej a=aC+b [°]. Po wstawieniu powyżej obliczonych danych otrzymano: a=(..............)*C[%]+(..................)[°], gdzie C- stężenie w procentach. Przeksztaucając równanie otrzymano:
, gdzie Cx oznacza wartość stężenia nieznanego roztworu. Wstawiając a=a0X otrzymano: Cx = ............ [%].

Błąd obliczono posługując się wzorem na różniczkę zupełną: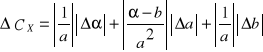
, gdzie błąd odczytu kąta Da=..........[]. Po wstawieniu danych: DCx = .......... [%].

Na podstawie uzyskanych danych wykonano wykres zależności kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu (patrz wykres). Wykres ten jest linią prostą.

5. Podsumowanie

W części pierwszej uzyskano następujące wyniki:

1.Kąt łamiący pryzmatu: fśr=.............. [°].

2.Kąt minimalnego odchylenia: s =................. [°]

3.Współczynnik załamania światła: n=.................

Porównując wynik z innymi współczynnikami można określić z jakiego szkła został wykonany pryzmat tj:

rodzaj szkła	n-lekkie	n-ciężkie
crown
flint
kwarcowe

Otrzymany wynik jest najbliżej szkła flint lekkiego, Lecz wielkość błędu z jakim obliczony został n nie pozwala ustalić tego jednoznacznie. Innymi czynnikami wpływającymi na niejednoznaczność pomiaru mogą być:

błędy przy nastawianiu obrazu szczeliny na celowniku lunetki (niedoskonałość oka),

niewłaściwe uchwycenie punktu zwrotnego prążka.

Wczęści drugiej ćwiczenia uzuskano dane do wykreślenia zależności kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu. Zależność ma charakter liniowy, a po aproksymacji serii wyników otrzymano prostą o równaniu: a=(................)*C+(..............) [°]. Przeksztaucając powyższy wzór obliczono nieznane stężenie roztworu sacharozy i ostatecznie otrzymano: Cx = .......... [%] . Wielkość błędu oblicona ze wzoru:
i wynosząca s=.......[%] oznacza, że błąd wyznaczenia stężenia jest bardzo duży.

9

---