Patryk Wołowicz

grupa 2

LABORATORIUM

PODSTAW MIERNICTWA

Ćwiczenie 4: Multimetry cyfrowe.

Celem tego ćwiczenia było zapoznanie się z różnymi metodami pomiaru napięcia, prądu, rezystancji, częstotliwości i określania stanów logicznych za pomocą multimetrów cyfrowych.

Ćwiczenie to było prowadzone pod nadzorem komputera, który zlecał kolejne zadania. Wydruk końcowy ćwiczenia jest dołączony do opracowania.

1. Wartość względnego błędu dyskretyzacji podczas pomiaru napięcia stałego.

Obliczanie względnego błędu dyskretyzacji wykonałem dla przedziału od 0 do 100 V.

Ogólnie względny błąd dyskretyzacji można obliczyć ze wzoru:

Rozdzielczość na danym zakresie obliczam poprzez wymnożenie zakresu miernika przez 0,0001 (miernik czterocyfrowy) i otrzymuję. Przykładowo mając zakres 10V rozdzielczość wynosi:

Jak widać rozdzielczość jest zawsze cztery rzędy wielkości mniejsza od zakresu pomiarowego.

Obliczenia miałem wykonać na zakresie od 0 do 100V co przedstawia tabela i wykres zamieszczone na następnej stronie.

Przy czym wykres dla wartości wskazań rzędu 0,01mV ma błąd dyskretyzacji rzędu 100%, więc dla zachowania przejrzystości zignorowałem błędy dla napięcia poniżej 1mV.

Tabela 1. Względny błąd dyskretyzacji miernika V-543.

Zakres 100mV i rozdzielczość 0,01mV.
U [mV]	10	20	30	40	50	60	70	80	90	100
δdysk [%]	0,1	0,05	0,033	0,025	0,02	0,017	0,014	0,013	0,011	0,01
Zakres 1V i rozdzielczość 0,1mV.
U [V]	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
δdysk [%]	0,1	0,05	0,033	0,025	0,02	0,017	0,014	0,013	0,011	0,01
Zakres 10V i rozdzielczość 1mV.
U [V]	1	2	3	4	5	6	7	8	9	10
δdysk [%]	0,1	0,05	0,033	0,025	0,02	0,017	0,014	0,013	0,011	0,01
Zakres 100V i rozdzielczość 10mV.
U [V]	10	20	30	40	50	60	70	80	90	100
δdysk [%]	0,1	0,05	0,033	0,025	0,02	0,017	0,014	0,013	0,011	0,01

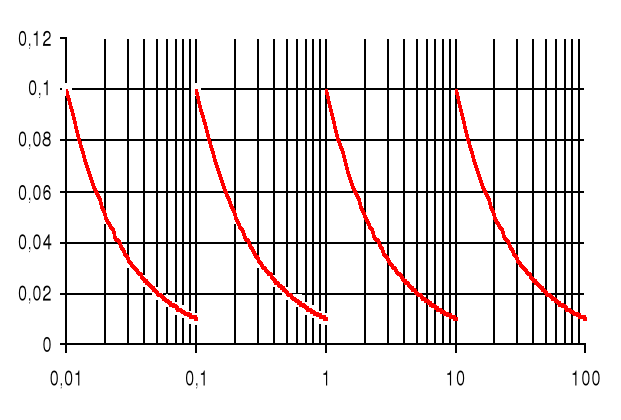
Rys 1. Wykres względnego błędu dyskretyzacji.

Jak widać błąd dyskretyzacji przy pomiarach z prawidłowymi zakresami pomiarowymi nie powinien przekroczyć wartości 0,1%.

2. Uzasadnienie wyników zadania drugiego.

W ćwiczeniu tym mierzyliśmy napięcie stałe w obecności zakłóceń pochodzących z generatora o częstotliwościach 50Hz, 75Hz i 100Hz. Jak można zauważyć z wykresów dla poszczególnych przebiegów, zakłócenia o częstotliwości 50 i 100Hz nie wpływają na zniekształcenie wartości badanego napięcia. Zakłócenie o częstotliwości 75Hz znacznie zniekształciło nam mierzoną wartość.

Dzieje się tak dlatego, ponieważ woltomierze cyfrowe są skonstruowane tak, aby eliminować zakłócenia pochodzące od sieci energetycznej. Odbywa się to poprzez odpowiedni dobór czasu całkowania integratora, który w naszych woltomierzach wynosi 20ms lub jest jego wielokrotnością. Czas ten wynika bezpośrednio z częstotliwości napięcia sieci energetycznej w Polsce, która wynosi 50Hz, a stąd jej okres 1/50Hz = 20ms.

Sygnał zakłócający wchodząc do integratora sumuje się z sygnałem napięcia stałego mierzonego przez miernik, czyli:

gdzie U_i jest napięciem na wejściu integratora, U_x napięciem stałym, a U_z sygnałem zakłócającym.

Na wyjściu z integratora:

Czas całkowania integratora pracującego w sieci wynosi 20ms. Niech t₀=0, natomiast t₁=20ms=0,02s.

Przyjmijmy teraz, że sygnał zakłócający ma częstotliwość 50Hz a stąd jego pulsacja ω=2πf=100π.

Napięcie wyjścia integratora:

czyli:

Widać więc, iż zupełnie zanikła nam składowa stała sygnału zakłócającego, a stąd wynika bezpośrednio wniosek, że układ całkujący jest odporny na zakłócenia o częstotliwości 50Hz. Podobne obliczenia otrzymujemy dla sygnału zakłócającego o częstotliwości 100Hz.

Co się dzieje, kiedy sygnał zakłócający ma częstotliwość 75Hz?

Można to zobrazować podstawiając taką częstotliwość do wzoru na napięcie wyjścia integratora. Otrzymujemy wówczas:

W tym przypadku widać bezpośrednio, iż nie zanikła nam składowa stała sygnału zakłócającego, stąd przebieg opuszczający integrator jest zniekształcony.

3. Obliczanie liczby impulsów prądowych n w jednym cyklu pomiarowym.

gdzie n jest ilością zliczonych impulsów, T_w okresem generatora wzorcowego, a f_x częstotliwością badanego przebiegu.

Dokonując przekształceń powyższego wzoru i przyjmując T_w=T_p, oraz f_x=f_wy otrzymuje się:

Podstawiając odpowiednie wartości do powyższego wzoru otrzymujemy:

Przy częstotliwości f_wy =0,62kHz liczba impulsów wynosi n = 124, natomiast dla f_wy =1,66kHz - n = 332.

---