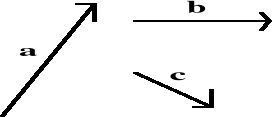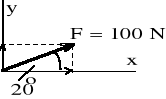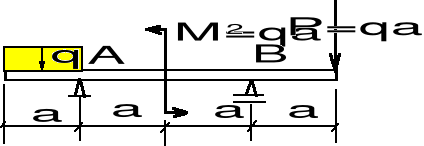WYKłADY Z MECHANIKI OGÓLNEJ

(dla studiów zaocznych)

Bogdan Wilczyński

Koszalin, 1993

I. WSTĘP DO MECHANIKI

I.1 Mechanika, jej rola i podział

Mechanika jest działem fizyki, zajmującym się badaniem ruchu ciał materialnych pod działaniem sił i ich mechanicznego oddziaływania. Podział mechaniki przedstawiono na rys. I.1.1.

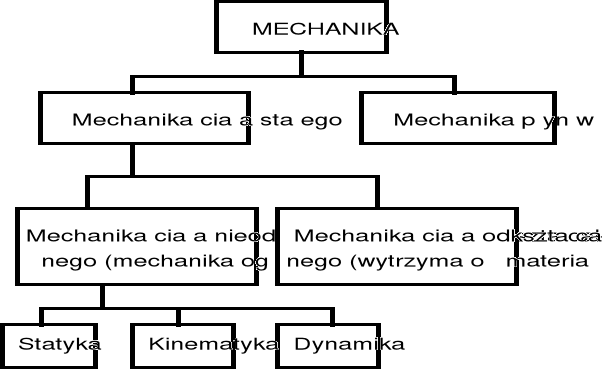
Rys. I.1.1.

Znaczenie mechaniki

1) dostarcza wiedzy niezbędnej do studiowania wytrzymałości i stateczności konstrukcji, drgań mechanicznych, teorii maszyn i mechanizmów,

2) uczy ścisłego myślenia.

Treścią naszych wykładów jest mechanika ogólna, zwana również mechaniką klasyczną, teoretyczną lub newtonowską. Mechanika ogólna bada ruch (spoczynek jest szczególnym przypadkiem ruchu) uproszczonych obiektów materii, takich jak: punkt materialny - punkt w sensie geometrycznym, któremu przypisano pewną masę, cialo sztywne - takie ciało, które pod działaniem sił nie zmienia swoich wymiarów geometrycznych.

Podział mechaniki ogólnej:

1. S t a t y k a - zajmuje się badaniem równowagi ciał,

2. K i n e m a t y k a - bada ruch bez uwzględnienia masy i przyczyn wywołujących ruch,

3. D y n a m i k a - bada ruch ciał w zależności od działania sił.

II.2 Elementy rachunku wektorowego

Rachunek wektorowy został stworzony szczególnie dla potrzeb mechaniki. Upraszcza on znacznie zapis matematyczny oraz ułatwia rozważania teoretyczne.

I.2.1. Skalar i wektor

Wielkości fizyczne występujące w mechanice są wielkościami skalarowymi i wektorowymi.

S k a l a r - wielkość dająca się przedstawić punktami skali, ,czyli podziałki liniowej. Przykładami wielkości skalarowych są: masa, objętość, praca, moc, czas.

W e k t o r - odcinek zorientowany w przestrzeni określony przez: 1) wartość (moduł), 2) kierunek i 3) zwrot. Przykładami wielkości wektorowych są: siła, moment, prędkość, przyspieszenie.

I.2.2. Podział wektorów

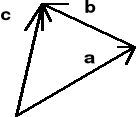
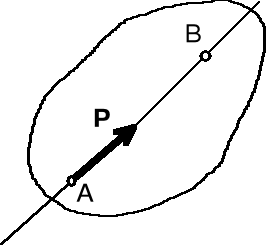
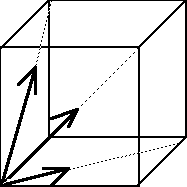
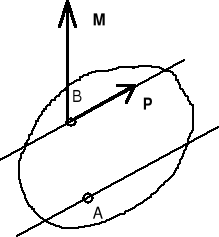
Wektory dzielimy na: 1) swobodne, jeśli jest obojętne, gdzie jest początek wektora (rys. I.2.1), 2) posuwne, jeśli początek wektora musi leżeć na pewnej prostej (rys. I.2.2) 3) związane, jeśli początek wektora jest określony (rys. I.2.3).

Rys. I.2.1 Rys. I.2.2 Rys. I.2.3

I.2.3. Działania na wektorach

I.2.3.1. Oznaczenia.

W druku wektor oznaczamy tłustą czcionką np. P, w notatkach (na tablicy) zwykłą literą z daszkiem, np. P. Wartość wektora oznaczamy zwykłą literą np. P.

I.2.3.2. Układ odniesienia.

Do opisu zjawisk fizycznych posługujemy się najczęściej prostokątnym układem odniesienia (rys. I.2.1)

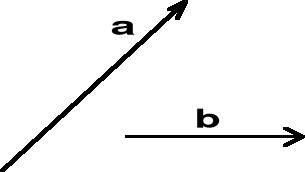
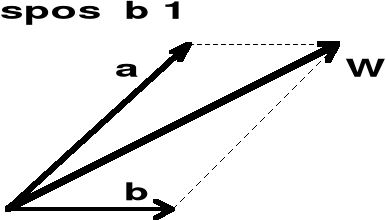
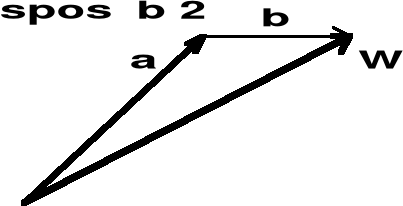
I.2.2.4. Dodawanie (składanie) wektorów

Dane są dwa wektory a i b. Szukamy wektora wypadkowego w = a + b (rys. I.2.4)

Rys. I.2.4.

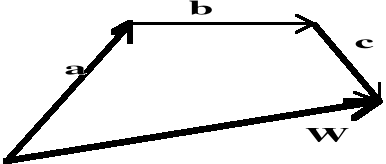
Jeśli mamy więcej wektorów (rys. I.2.5)

Rys. I.2.5

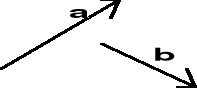
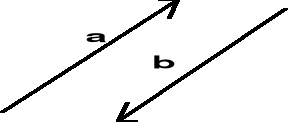
I.2.3.5. Wektory przeciwne

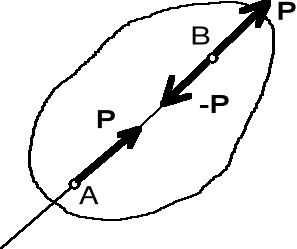
Wektorem przeciwnym do wektora a nazywamy wektor b, którego wartość i kierunek są takie same jak wektora a, natomiast zwrot jest przeciwny. Zapisujemy b = - a (rys. I.2.6).

Rys. I.2.6

I.2.3.6. Odejmowanie wektorów

Aby odjąć wektor b od wektora a należy do wektora a dodać wektor przeciwny do wektora b, t.j. c = a-b = a+(-b)(rys. I.2.7)

Rys. I.2.7

I.2.3.7. Rozkład wektora na kierunki

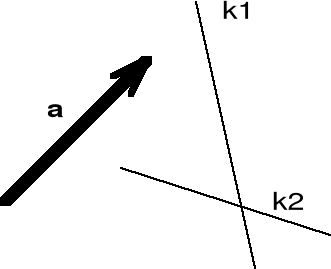
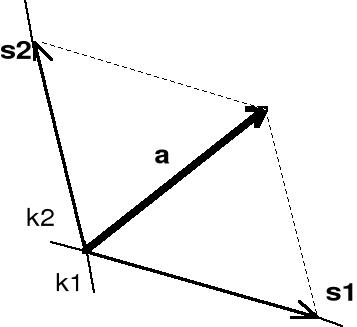
Dany jest wektor a oraz dwa kierunki k1 i k2 . Wektor a = s1 + s2 (rys.I.2.8):

Rys. I.2.8

I.2.3.8. Równość wektorów.

Dwa wektory są równe, co zapisujemy a = b, jeśli wszystkie elementy mają równe.

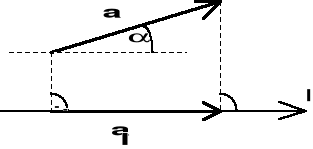
I.2.3.9. Rzut wektora na oś.

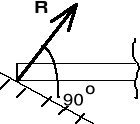
Rzutem prostokątnym wektora a na oś l nazywamy wektor al, którego początkiem jest rzut początku wektora a, natomiast końcem jest rzut końca wektora a. Miarę rzutu a nazywamy krótko składową. Składowa ma znak + , gdy rzut jest zgodny z osią, -, gdy rzut nie jest zgodny z osią (rys. I.2.9).

Rys. I.2.9

Przykład

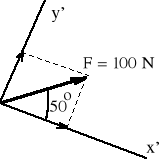
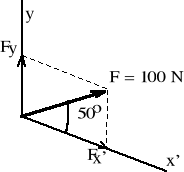
Siła F = 100 N działa pod kątem = 20o do poziomu (osi x). Dane są dwa układy współrzędnych xy i x'y'. Osie układu x'y' są obrócone o kąt 30o względem układu xy. Wyznaczyć składowe siły F na kierunkach: (1) xy, (2) x'y', (3) x'y.

Rozwiązanie

1) 2) 3)

Fx = 100 cos20 = 94.0 N Fy = 100 sin20 = 34.2 N	Fx' = 100 cos50 = 64.3 N Fy' = 100 sin50 = 76.6 N	Fx' = 100 0.94/0.87 = 108.5 N Fy = 100 0.77/0.87 = 88.5 N

I.2.3.10. Iloczyn skalarny

Iloczyn skalarny dwóch wektorów oznaczamy c = a b = a b cos(a,b)

Własność: a b = b a.

Przypadki szczególne: a b = 0, gdy a b, a b = ab, gdy a b.

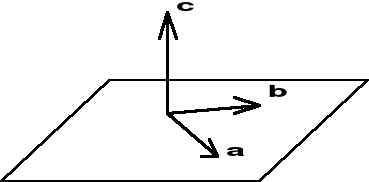
I.2.3.11. Iloczyn wektorowy

Wektor c jest iloczynem wektorowym wektorów a i b, co zapisujemy c = a * b o własnościach:

1) moduł c = ab sin(a,b),

2) kierunek c a oraz c b,

3) zwrot c taki, że wektory a,b,c stanowią układ prawoskrętny (rys. I.2.10).

Rys. I.2.10

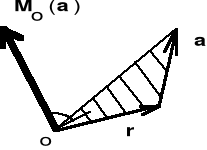
I.2.3.12. Moment wektora względem punktu

Momentem wektora a względem punktu O jest wektor

Mo (a) = r * a,

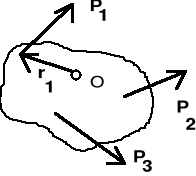
gdzie r jest wektorem, którego początek znajduje się w punkcie O, zaś koniec jest jednocześnie początkiem wektora a (rys.I.2.11).

Rys. I.2.11

II. STATYKA

II.1. Pojęcie siły

S i ł a - oddziaływanie jednego ciała na drugie. Druga definicja - każda przyczyna wprawiajaca ciało w ruch. Siła jest wielkością wektorową.

U k ł a d s i ł - kilka sił działających na ciało.

II.1.1. Klasyfikacja sił

Siły działające na ciało dzielimy na:

1) Siły zewnętrzne - pochodzą od oddziaływania obcych ciał na ciała rozpatrywanego układu materialnego.

2) Siły wewnętrzne - pochodzące od wzajemnego oddziaływania ciał danego układu.

II.1.2.,Podział sił zewnętrznych

Siły zewnętrzne dzielimy na s i ł y c z y n n e starające się wprawić ciało w ruch i si- ł y b i e r n e przeciwdziałające ruchowi (reakcje).

II.1.3. Układ sił

U k ł a d s i ł - jeśli na ciało działa kilka sił, nazywamy je układem sił.

II.2. Zadania statyki

- zastąpienie układu sił układem prostszym (redukcja układu sił),

- określenie warunków równowagi ciała sztywnego.

II.3. Zasady statyki

Z a s a d a (pewnik, aksjomat) - pewna prawda przyjęta na podstawie obserwacji zjawisk fizycznych. Zasady nie można udowodnić teoretycznie, ale można wykazać jej słuszność na podstawie doświadczenia.

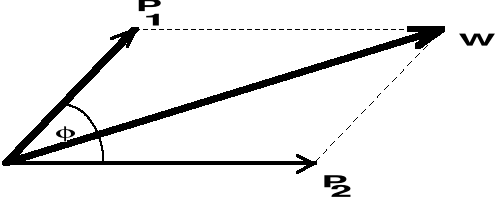
Zasada równoległoboku.

Dwie siły przyłożone do jednego punktu możemy zastąpić siłą wypadkową przyłożoną do tego punktu, będącą przekątną równoległoboku utworzonego na tych siłach.

	W = P1 + P2
	W = P1 + P2 W = P1 - P2

Zasada równowagi.

Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy, gdy działają wzdłuż jednej prostej, są przeciwnie skierowane i mają tę same wartości liczbowe (dwójka zerowa).

P2 = - P1

P1 = P2

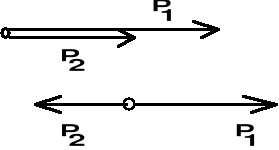
Zasada dołączania i odejmowania sił będących w równowadze.

Działanie układu sił nie ulegnie zmianie, gdy dodamy do niego lub odejmiemy układ sił równoważących się (dwójkę zerową)

Zasada oswobodzania od więzów.

Każde ciało nieswobodne możemy myślowo oswobodzić oswobodzić od więzów, zastępując ich oddziaływanie siłami reakcji (krótko, reakcjami) i traktować jako swobodne pod działaniem sił czynnych i reakcji więzów.

II.4. Więzy i ich reakcje

W i ę z a m i nazywamy czynniki ograniczające ruch ciała.

C i a ł o s w o b o d n e - takie ciało, które może wykonywać dowolne ruchy wywołane siłami czynnymi

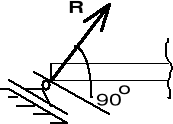
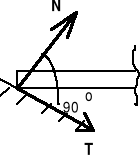
W punkcie zetknięcia się danego ciała z powierzchnią na ciało działa siła reakcji R, którą możemy rozłożyć na dwie składowe: normalną do powierzchni N, oraz styczną T, zwaną siłą tarcia.

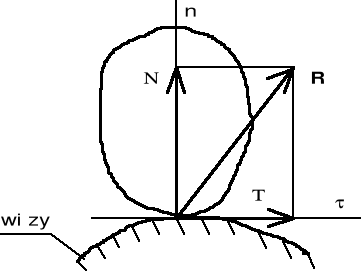
Więzy dzielimy na:

a) idealne,

b) rzeczywiste.

Takie więzy w których nie występuje tarcie nazywamy więzami idealnie gładkimi.

Ponieważ w dalszym ciągu zajmować się będziemy głównie zagadnieniami płaskimi, będziemy mieli do czynienia z następującymi grupami więzów:

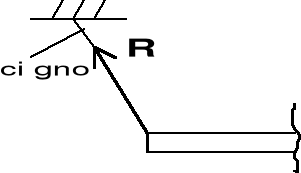
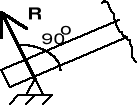
1. Więzy o jednej niewiadomej (rys. II.4.1)

a) podparcie na idealnie gładkiej powierzchni,

b) podparcie na podporze przesuwnej (łożysku ruchomym),

c) zawieszenie na wiotkim cięgnie

d) podparcie na ostrzu lub ostrej krawędzi,

a) b) c) d)

Rys. II.4.1

2. Więzy o dwóch niewiadomych (rys. II.4.2)

a) podparcie na powierzchni chropowatej,

b) podparcie na podporze stałej (łożysko stałe).

a) b)

Rys. II.4.2

3. Więzy o trzech niewiadomych - utwierdzenie sztywne (rys. II.4.3)

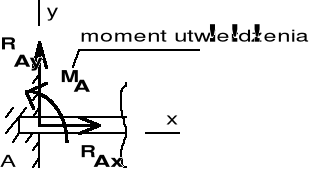
Rys. II.4.3

II.5. Klasyfikacja układów sił

Układy sił dzielimy na dwie podstawowe grupy:

1) układy sił zbieżnych,

2) układy sił dowolnych.

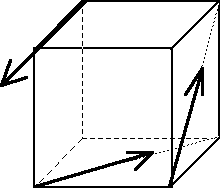
Układy sił zbieżnych charakteryzują się tym, że ich linie działania przecinają się w jednym punkcie. Jeśli tylko jedna z linii nie ma z pozostałymi punktu wspólnego, to taki układ sił nazywamy dowolnym.

Gdy linie działania sił leżą w jednej płaszczyżnie, to takie układy sił nazywamy płaskimi.

Mamy więc (rys. II.5.1):

1) układ sił płaski zbieżny,

2) układ sił płaski dowolny,

3) układ płaski sił równoległych (szczególny przypadek układu płaskiego dowolnego)

1) 2) 3)

Rys. II.5.1

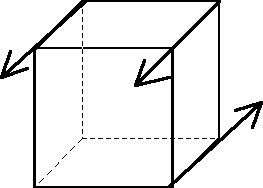
W ogólności mamy (rys. II.5.2):

1) układ sił przestrzenny zbieżny,

2) układ sił dowolny,

3) układ przestrzenny sił równoległych (szczególny przypadek układu sił dowolnego).

1) 2) 3)

Rys. II.5.2

II.6. Redukcja układu sił zbieżnych

II.6.1. Redukcja na drodze geometrycznej

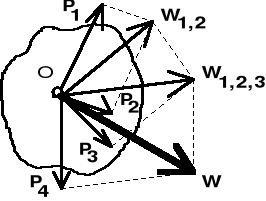
Wykorzystując zasadę równoległoboku wykażemy, że układ sił zbieżnych redukuje się do jednej siły, zwanej w y p a d k o w ą (rys.II.6.1a). Dla wygody rozpatrujemy układ płaski sił zbieżnych.

a) b)

Rys. II.6.1

Istnieje również drugi znany nam sposób (rys. II.6.1b). Taką konstrukcję nazywamy wielobokiem sił.

II.6.2. Redukcja na drodze analitycznej

Podstawą redukcji układu sił zbieżnych jest twierdzenie o rzucie wypadkowej.

Rzut wypadkowej na dowolną oś równy jest sumie rzutów poszczególnych sił składowych (rys. II.6.2).

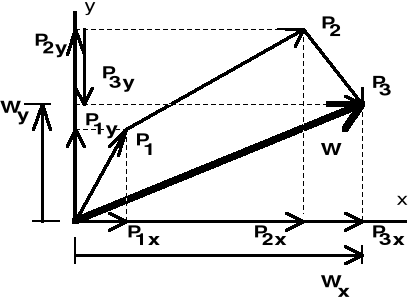
Rys. II.6.2

Dany jest układ sił przestrzenny zbieżny. Rzutując wszystkie siły na poszczególne osie mamy:

,

,

.

Mając składowe wypadkowej możemy obliczyć jej moduł oraz kosinusy kierunkowe:

cos(W,x) =
, cos(W,y) =
, cos(W,z) =
.

II.7. Warunki równowagi układu sił zbieżnych

Warunkiem równowagi układu sił zbieżnych jest zerowanie się wypadkowej.

Stąd warunek geometryczny równowagi W = 0, a warunki analityczne równowagi przedstawiają się następująco:

,
,
.

Dla układu sił płaskiego zbieżnego obowiązują dwa pierwsze równania równowagi.

,
.

Przykład 1

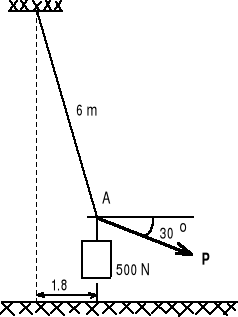
Z jaką siłą P musi ciągnąć linę człowiek, aby trzymać ciężar 500 N w położeniu jak na rysunku ?

Rys.

Rozwiązanie

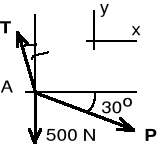
Układ sił jest układem płaskim zbieżnym.

Równania równowagi:

X = -T sin + P cos30o = 0,

Y = T cos - 500 - P sin30o = 0.

Z danych na rysunku: sin = 1.8/6.0, = 17o30'.

Z pierwszego równania wyznaczamy siłę T i podstawiamy ją do drugiego równania.

Z drugiego równania otrzymujemy ostatecznie, że:

P = 221.8 N.

Przykład 2

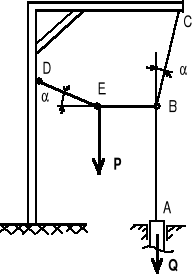
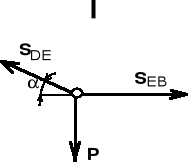
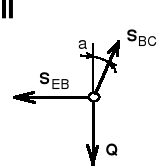
W celu wyciągnięcia pala z ziemi zbudowano układ składający się ramy wspornikowej i odpowiednio połączonych cięgien (patrz rys.). Opór jaki stawia pal (ciężar pala + tarcie gruntu o pal) wynosi 10 kN. Jaką siłę należy przyłożyć w punkcie E, aby wyciągnąć pal z gruntu.

Rys.

Rozwiązanie

Układ przedstawiony na rys. jest układem złożonym i możemy go rozłożyć na dwa podukłady sił zbieżnych.

Równania równowagi dla podukładu II:

X = - SEB + SBC sin = 0

Y = - Q + SBC cos = 0.

Stąd: SBC = Q/cos, SEB = Q tg.

Równania równowagi dla podukładu I:

X = - SDE cos + SEB = 0

Y = SDE sin - P = 0.

Stąd:

SDE = SEB /cos = Q tg/cos,

P = Q tg sin/cos = Q tg 2.

Na przykład:

dla tg = 0.1, co odpowiada kątowi = 6o P = 1 kN.

II.8. Redukcja dowolnego układu sił

Zanim przystąpimy do omawiania zagadnienia redukcji układu sił dowolnego, podamy niezbędne definicje i twierdzenia: pojęcie pary sił, momentu siły względem punktu, momentu siły względem osi, twierdzenie o równoległym przesunięciu siły oraz twierdzenie o momencie wypadkowej.

II.8.1. Para sił. Własności pary sił.

Parą sił nazywamy dwie siły leżące na dwóch równoległych, niepokrywających się prostych o jednakowych modułach, lecz przeciwnych zwrotach.

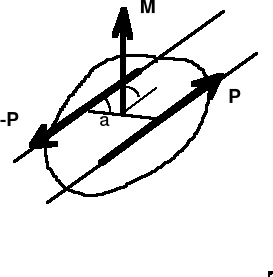
Własności pary sił:

1) rzut pary sił na dowolną oś jest równy zeru,

2) moment pary sił nie zależy od punktu względem którego go liczymy i jest równy iloczynowi modułu jednej z sił razy odległość pomiędzy liniami działania sił (moment pary sił jest wektorem swobodnym),

3) każdą parę sił można zastąpić inną parą sił zachowując moment niezmieniony.

II.8.2. Moment siły względem punktu

Momentem siły P względem punktu O nazywamy iloczyn wektorowy wektora r przez wektor siły P, gdzie r jest wektorem poprowadzonym od punktu O do punktu przyłożenia siły P (rys. II.8.1)

M = r x P, M = P rsin = P a

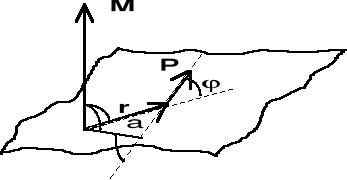
Rys. II.8.1

II.8.3. Moment siły względem dowolnej osi

Momentem siły P względem osi l nazywamy moment rzutu P' siły P na płaszczyznę prostopadłą do osi l, mierzony względem punktu przebicia tej osi z płaszczyzną (rys. II.8.2)

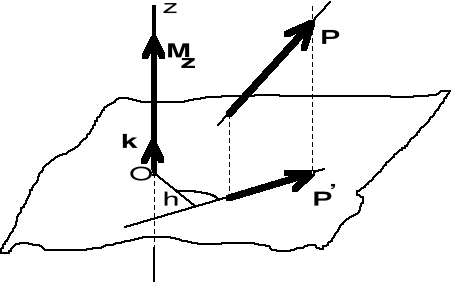
Rys. II.8.2

II.8.4. Twierdzenie o równoległym przesunięciu siły

Podstawą redukcji układu sił dowolnie zorientowanych w przestrzeni jest twierdzenie o równoległym przesunięciu siły.

Siłę możemy przesuwać równolegle w płaszczyżnie jej działania dodając parę sił.

II.8.5. Twierdzenie o momencie wypadkowej (tw. Varignona)

Moment wypadkowej równa się sumie momentów poszczególnych sił składowych.

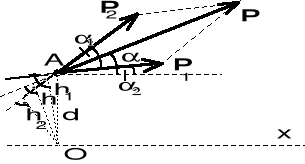
M10 = P1 h1 , M20 = P2 h2, M0 = P h.

Ponieważ: h1 = d cos1, h2 = d cos2, h = d cos,,

M10 = P1 d cos 1, M20 = P2 d cos 2, M0 = P d cos .

Z drugiej strony

P1 cos1 = P1x, P2 cos2 = P2x, P cos = Px,

zatem:

M10 = P1x d, M20 = P2x d, M0 = Px d,

a ponieważ: Px = P1x + P2x,

więc:

M0 = P1X d + P2x d = M10 + M20, co trzeba było wykazac.

II.8.6 Redukcja układu sił dowolnych na drodze geometrycznej

Dany jest układ n sił działałących na ciało sztywne (rys. II.8.3). Obieramy pewien dowolny punkt O zwany biegunem redukcji. Przesuwamy kolejno siły do zaczepione w różnych punktach ciała do bieguna redukcji. Pamiętamy, że przesuwając siłę musimy dodać parę sił (patrz twierdzenie o równoległym przesunięciu siły).

Rys.II.8.3

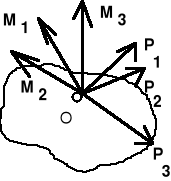
W biegunie redukcji otrzymujemy dwa pęki wektorów: pęk wektorów sił P1, P2,....,Pn (tu n=3), oraz pęk wektorów par sił M1, M2,....,Mn. Siły P1, P2,....,Pn (siły zbieżne w jednym punkcie) zastępujemy jedną siłą wypadkową W.

Podobnie pary sił M1, M2,....,Mn składamy w jedną parę sił M zwaną momentem głównym.

W n i o s e k. Dowolny układ n sił redukuje się do wypadkowej W (zwanej też siłą główną) oraz do momentu głównego M.

II.8.7. Redukcja układu sił dowolnych na drodze analitycznej

W biegunie redukcji przyjmujemy układ współrzędnych prostokątnych x,y,z. Z twierdzenia o rzucie wypadkowej mamy:

,

,

,

natomiast z twierdzenia o momencie wypadkowej mamy:

,

,

,

Mając składowe wypadkowej oraz składowe momentu głównego możemy wyznaczyć moduł wypadkowej, moduł momentu głównego oraz odpowiednie kosinusy kierunkowe (patrz II.6.2.).

Przykład obliczania momentu względem osi x,y,z

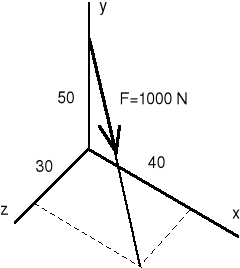
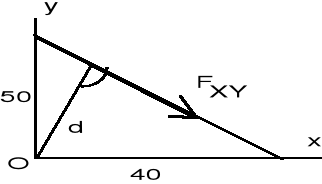
Siła F = 1000 N przyłożona jest w punkcie A (0, 0, 50) i skierowana do punktu B (40, 0, 30). Wyznaczyć składową M momentu od siły F. Wymiary podano w [m] (rys. 1.5).

Rys. 1.5

Rozwiązanie

Zadanie można rozwiązać dwoma sposobami.

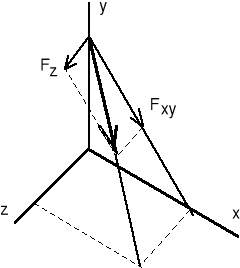
Sposób (1). Wykorzystujemy definicję momentu względem dowolnej osi. W tym celu rozkładamy siłę F na składowe F i F (rys 1.5). Składowa F jest równoległa do osi z, więc tylko składowa F daje moment względem osi z

M = F d,

gdzie d jest najkrótszą odległością linii działania F od punktu O i wynosi:

Składowa F wynosi: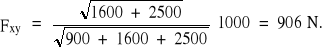

Ostatecznie mamy:

M = 906 31.2 = 28300 Nm.

Sposób (2). Siłę F rozkładamy na trzy składowe. Składowych F i F nie obliczamy, gdyż pierwsza leży na osi z, a druga ją przecina.

Rzut F wynosi:

Stąd: M = F OA = 566 50 = 28300 Nm.

II.9. Warunki równowagi układu sił dowolnych

II.9.1. Warunki geometryczne

Aby dowolny układ sił był w równowadze wypadkowa W oraz moment M muszą być równe zeru (warunek konieczny i dostateczny)

W = 0, M = 0.

II.9.2. Warunki analityczne

Zerowanie się wektorów wypadkowej W oraz momentu M pociąga za sobą zerowanie się ich składowych, co zapisujemy w postaci 6-ciu równań równowagi:

,
,
.

,
,
.

Jeśli siły działają w jednej płaszczyżnie, to liczba równań równowagi redukuje się do 3-ch:

,
,
.

Dla układu przestrzennego sił równoległych mamy następujące r-nia:

,
,

a dla układu płaskiego sił równoległych tylko 2 r-nia równowagi:

,

Przykład

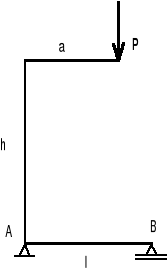
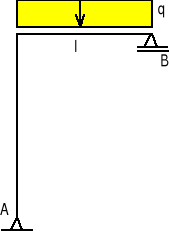
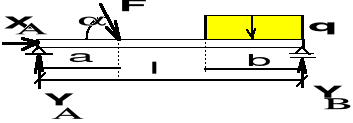
Belkę obciążono i zamocowano jak na rys. Wyznaczyć reakcje belki dla następujących danych: l = 3 m, b = 1 m, a = 1 m, q = 2 kN/m, F = 4 kN, a = 60 .

Rys.

Rozwiązanie

Początek układu współrzędnych przyjmujemy w punkcie A. Oś x jest skierowana wzdłuż osi belki, a oś y jest do niej prostopadła. Z oznaczeń na rys. wynika, że na lewy koniec belki nałożono więzy w postaci podpory przegubowej stałej, a w punkcie B w postaci podpory przesuwnej.

Równania równowagi:

(X = 0) 4 cos60o + XA = 0,

( = 0) - 4 sin60o + YA + YB - 2x1 = 0,

(MA = 0) - 4 sin60o 1 - 2 x1 x 2.5 + YB x 3 = 0.

Po rozwiąząniu układu równań równowagi otrzymujemy następujące wartości składowych reakcji podpór:

XA = - 2 kN, Ya = 2.64 kN, Yb = 2.82 kN.

Zadanie

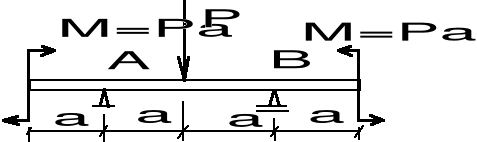
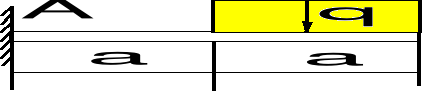
Wzorując się na powyższym przykładzie wyznaczyć reakcje belek przedstawionych na poniższych rysunkach.

a) b) c)

d) e) f)

Rys.

Rozwiązania

(a) Belka jest dwukrotnie statycznie niewyznaczalna (składowe reakcji YA, YB, YC, MC), więc nie jest możliwe rozwiązanie zadania przez ułożenie wyłącznie równań równowagi. Muszą być ułożone dodatkowe równania (patrz kurs Wytrzymałości materiałów).

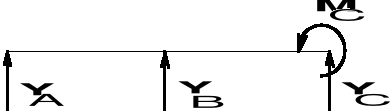
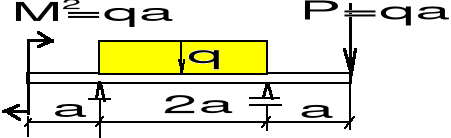
(b) Belka jest statycznie wyznaczalna.

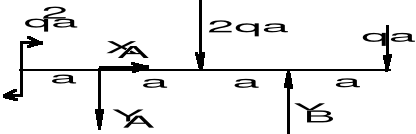
Możemy ułożyć następujące równania równowagi:

(Y = 0) YA + YB--- q2a - qa = 0,

(MA = 0) - qa - q2a a - qa 3a + Y a = 0.

Stąd:

YB = 6 qa, YA = - 3 qa.

c) - f) Porównaj rozwiązanie wariantu b).

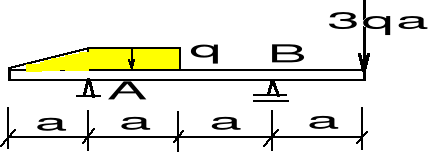
Przykład

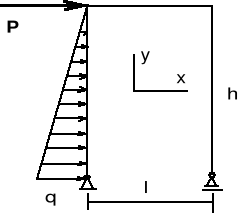
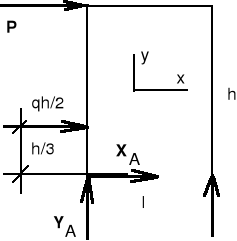
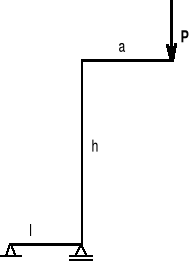
Wyznaczyć reakcje podpór sztywnej ramy (rys.) poddanej działaniu poziomej siły P i rozłożonej, w postaci trójkąta. Dane liczbowe: P = 2 kN, q = 0.2 kN/m, h = 3 m, l = 1.5 m.

Rys.

Rozwiązanie

Przyjmując układ współrzędnych jak na rys. zapisujemy następujące równania równowagi:

(X = 0)

(Y = 0)

(M = 0)

Po rozwiązaniu układu równań otrzymujemy:

X = - 2.3 kN, Y = - 4.2 kN, Y = 4.2 kN.

Zadanie

Wyznaczyć reakcje ram statycznie wyznaczalnych pokazanych na rys. a - rys. d.

a) b) c) d)

Rys.

Przykład

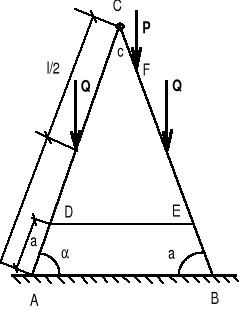
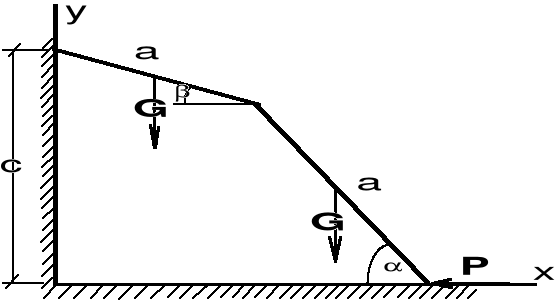
Drabina składa się z dwóch członów AC i BC o ciężarze Q i długości l każdy, połączonych przegubem w punkcie C oraz liną DE (rys. 3.7). Drabina stoi na gładkiej podłodze, a w punkcie F stoi człowiek o ciężarze P. Dane: AD = BE = a, CF = c, oraz kąt a pomiędzy poszczególnymi członami a podłogą.

Rys.

Rozwiązanie

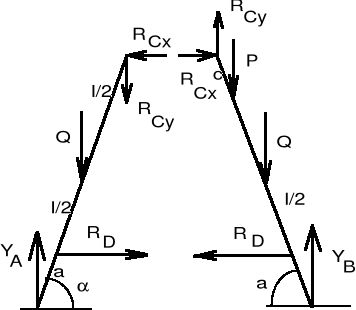
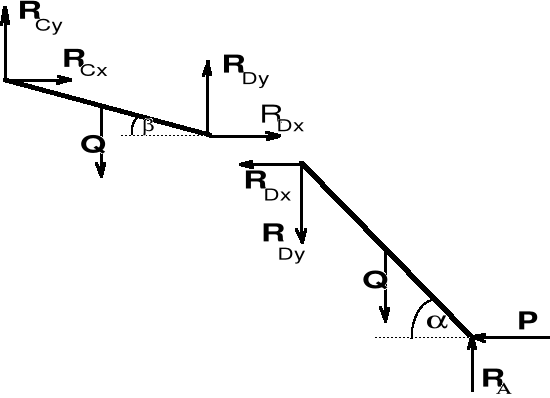
W punktach A i B przykładamy siły reakcji YA i YB. Ponadto rozcinamy cięgno przykładając w miejscu przecięcia siły RD, - RD. Siłę RC pochodzącą odwzajemnego oddziaływania członów AC i BC rozkładamy na kierunki przyjętego układu współrzędnych. Otrzymujemy w ten sposób dwa podukłady sił płaskich dowolnych (rys. b, rys. c).

Mamy łącznie do wyznaczenia 5 niewiadomych YA, YB, RD, RCx, RCy, a dla każdego podukładu możemy ułożyć po 3 równania równowagi. Zatem liczba niewiadomych nieprzekracza liczby równań równowagi. Układ sił działających na drabinę jest układem statycznie wyznaczalnym.

Uwaga! Zwroty składowych reakcji w przegubie C przyjmujemy dowolnie, ale zgodnie z zasadą wzajemnego oddziaływania ciał należących do rozpatrywanego układu sił. Możliwe są więc następujące kombinacje:

itp.

Równania równowagi:

Podukład (1):

X = - RCx + RD = 0,

Y = YA - Q - RCy = 0,

MC = - YA l cosa + Q l/2 cosa + RD (l - a) sina = 0,

Podukład (2):

X = RCx - RD = 0,

Y = RCy - P - Q + YB = 0

Przykład

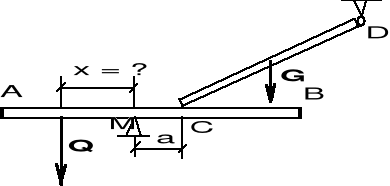
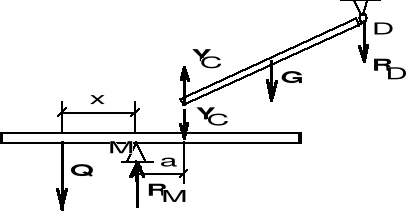
Na dżwigni równoramiennej umocowanej przegubowo w punkcie M zawieszono ciężar Q. W punkcie C opiera się o dżwignię koniec pręta o ciężarze G,zamocowany przegubowo w punkcie D. Dane: MC = a oraz ciężary Q i G. Znależć ME = x w jakiej należy zawiesić ciężar Q, aby była zachowana równowaga.

Rys.

Rozwiązanie

Kąt pomiędzy belką CD a belką AB oznaczamy przez a, oraz przyjmujemy długość belki CD = l. Wielkości te nie są dane i ulegną uproszczeniu w przekształceniach algebraicznych. Ponieważ układ przedstawiony na rys. jest układem złożonym, rozkłada-my go na dwa podukłady proste. Aby wyznaczyć szukane ME = x, wystarczy ułożyć 2 równania równowagi: równanie momentów względem punktu D (dlaczego?) dla belki CD, oraz równanie momentów względem podpory M (z tego samego powodu) dla belki AB.

G l/2 cosa - YC l cosa = 0.

Stąd:

YC = - G/2.

Q x = YC a.

Stąd:

x = YCa/Q = Ga/2Q.

Wyjaśnienie. Układamy równania momentów względem punktów C i M aby nie wprowadzać do równań niewiadomych reakcji.

Przykład

Dwie jednorodne belki o ciężarze Q i długości l każda połączone przegubowo w punkcie C oparto na dwóch idealnie gładkich kołkach jak pokazuje rys. obliczyć kąt w położeniu równowagi, oraz reakcje w punktach podparcia D i E.

Wskazówka! Układ jest złożony i symetryczny względem osi pionowej.

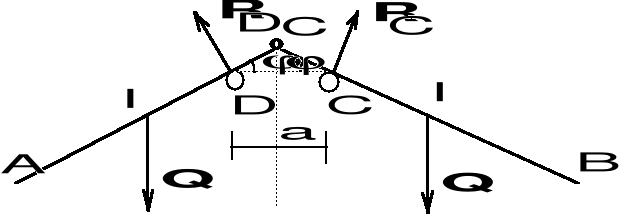
Rys.

Rozwiązanie

Układ złożony rozkładamy na układy proste, z tym, że z uwagi na warunki zadania nie musimy układać kompletu równań dla każdego podukładu. Zadanie możemy rozwiązać następująco:

Z racji symetrii:

RD = RE .

Następnie, możemy ułożyć jedno równanie równowagi dla całego układu, np, Y = 0:

2 RD cosv - 2 Q = 0.

Uwaga! Składowe reakcji w punkcie C nie wchodzą do równań równowagi ułożonych dla całego układu.

Trzecie równanie równowagi (mamy trzy niewiadome) możemy ułożyć dla jednego z podukładów, np. z lewej strony (patrz rys. ). Aby nie wprowadzać do równań niewiado-mych reakcji przegubu C, układamy równania momentów względem tego przegubu.

- RDa/cos + Q l/2 cos = 0.

Po rozwiązaniu układu powyższych równań otrzymujemy:

= RD = RE =

Pozornie, zadanie wydaje się być skomplikowane, ale ułożenie odpowiednich równań równowagi szybko prowadzi do żądanego wyniku.

Przykład

Dwa jednakowe pręty AB i BC, o ciężarze Q każdy, połączone są przegubem B. Koniec C pręta BC połączony jest przegubowo do pionowej ściany, zaś koniec A pręta AB opiera się o gładką płaszczyznę poziomą. Dana jest odległość OC = c. Oba pręty znajdują się w jednej płaszczyżnie pionowej. Jak wielką siłę poziomą trzeba przyłożyć w punkcie A aby pręt AB tworzył z poziomem kąt ?

Rys.

Rozwiązanie

Aby rozwiązać zadanie przy pomocy jak najmniejszej liczby równań postępujemy następująco:

Układamy równanie momentów względem punktu C:

MC = - P (a sin + a sin) + G a/2 cos + G (a cos +

+ a/2 cos) + RA (a cos + a cos) = 0.

Ponieważ do powyższego równania weszła niewiadoma reakcja RA układamy równanie momentów względem punktu B dla podukładu (2). W ten sposób unikamy wprowadzenia do równań kolejnych niewiadomych.

M = - P a sin - G a/2 cos + RA a cos = 0.

Kąt jest znany, gdyż może być wyznaczony z równania więzów:

c = a sin + a sin.

Stąd: sin = (c-asin)/a) , = arcsin[(c-asin)/a].

Po rozwiązaniu układu równań otrzymujemy ostatecznie:

, tg tg.

Przykład

Wyznaczyć reakcje podpór A, B i D oraz reakcję w przegubie C belki przegubowej (belka gerberowskiej) pokazanej na rys.

Rys.

Belkę przegubową rozkładamy na dwa podukłady: belkę AC i belkę CD.

Równania równowagi dla podukładu (1):

(X = 0) XA - XC = 0,

(Y = 0) YA + YB -YC= 0,

(MA = 0) YB a - YC (l - b) = 0.

Równania równowagi dla podukładu (2):

(X = 0) XC - RD sina = 0,

(Y = 0) -qb + RD cosa + YC = 0,

(MC = 0) RD cos b - qb2/2 - = 0.

Po rozwiązaniu układu równań i podstawieniu danych liczbowych otrzymujemy:

XA = 0.29 kN, YA = - 0.50 Kn, XB = 0.29 kN,

YC = + 0.50 kN, XC = 1.0 kN, RD = 0.58 kN.

---