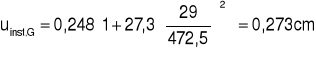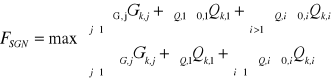
(EC0 - 6.4.3.2 wz. 6.10a i 6.10b)
BELKA ZŁOŻONA ŁĄCZONA NA GWOŹDZIE
Zaprojektować jednoprzęsłową belkę stropową o przekroju dwuteowym wykonaną z elementów z drewna sosnowego łączonych na gwoździe.
Dane:
Rozpiętość belki L = 4,50 m,
Klasa użytkowania 1 Rozstaw belek a = 1,0 m
Gwoździe okrągłe, gładkie. ksys = 1,0
1.Właściwości drewna (PN-EN 338:2009)
Klasa wytrzymałości C30
Wytrzymałość charakterystyczna na zginanie fm,k = 30 MPa = 3,0 kN/cm2
Wytrzymałość charakterystyczna na ścinanie fv,k = 4,0 MPa = 0,4 kN/cm2
Wytrzymałość charakterystyczna na rozciąganie ft,0.k = 18 MPa = 1,8 kN/cm2
Wytrzymałość charakterystyczna na ściskanie
w poprzek włókien fc,90,k = 2,7 MPa = 0,27kN/cm2
Średni moduł sprężystości wzdłuż włókien E0,mean = 12 GPa = 1200 kN/cm2
5% kwantyl modułu sprężystości
wzdłuż włókien E0,05 = 8,0 GPa = 800 kN/cm2
Gęstość charakterystyczna ρk = 380 kg/m3
Gęstość średnia ρm = 460 kg/m3
2. Kombinacje oddziaływań, maksymalne siły przekrojowe
a) stan graniczny użytkowalności
Obciążenia charakterystyczne:
- stałe Gk = gkxa = 0,8x1,0 = 0,8 kN/m
- użytkowe Qk = qkxa = 1,5x1,0 = 1,50 kN/m
b) stan graniczny nośności
Należy przyjąć mniej korzystną z dwu kombinacji podstawowych:
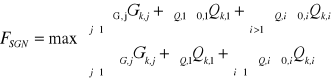
(EC0 - 6.4.3.2 wz. 6.10a i 6.10b)
W tym przypadku:
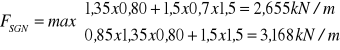
FSGN = 3,168 kN/m
Dla 1 klasy użytkowania współczynniki modyfikujące kmod wynoszą (EC5 - tabl. 3.1):
dla obciążenia stałego kmod,st = 0,6
dla obciążenia średniotrwałego kmod,śr = 0,8
Obciążenia obliczeniowe:
- stałe gd = γGxGk = 1,35x0,8 = 1,08 kN/m
- użytkowe pd = γQx Qk = 1,5x1,50 = 2,25 kN/m
Miarodajna kombinacja obciążeń odpowiada maksymalnej wartości:
max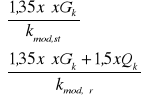
max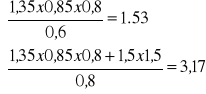
Miarodajna jest pełna kombinacja obciążeń i współczynnik modyfikujący odpowiadający obciążeniu średniotrwałemu (o najkrótszym okresie trwania w przyjętej kombinacji obciążeń) (EC5 - 3.1.3(2)), tj. kmod = 0,8.
Rozpiętość obliczeniowa: lo = 1,05l = 1,05x4,50 = 4,725 m.
Maksymalny moment zginający Md = 0,125x3,168x4,7252 = 8,8409kNm ≈ 884KNcm
Maksymalna siła poprzeczna Vd = 0,5x3,168x4,725 = 7,48 kN
3. Dobór przekroju belki
Przyjęto gładkie gwoździe o średnicy d = 4,5 mm i średnicy główki dh = 10,5 mm. (Tablica Z-7.4.1-1 PN-B-03150:2000),
Przed osadzeniem gwoździ należy nawiercać otwory, jeżeli grubość elementów drewnianych jest mniejsza niż:
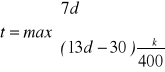
(EC5 - 8.3.1.2(6))
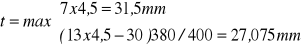
t ≥ 31,5 mm
Przyjęto grubość półki 45 mm (osadzanie gwoździ bez nawiercania otworów).
Długość zakotwienia gwoździa lpen powinna wynosić co najmniej 8d (8.3.1.2.(1))
Przyjęto: lpen= Lgw - t - 1mm
Minimalna długość gwoździa Lgw (gdy lpen = 8d):
Lgw ≥ lpen +t + 1 mm;
Lgw ≥ 8x4,5 +45 +1 = 82 mm.
Przyjęto gwoździe 45/100, dh = 10,5 mm
Rozstaw gwoździ wzdłuż włókien:
(Tablica EC5- 8.2 dla ρk ≤ 420 kg/m3 i α = 0o)
a1min = (5 + 5cosα)d = 10d=10x4,5 = 45 mm,
Przyjęto a1 = 60 mm; Gwoździe będą wbijane w dwóch szeregach (nsz = 2).
Równoważny rozstaw gwoździ teoretycznie rozłożonych w jednym szeregu:
s1 = a1/nsz = a1/2 = 30 mm z przesunięciem o d wzdłuż włókien.
UWAGA: Jeżeli a1 < 14 d, nośność gwoździ należy wyznaczać uwzględniając efektywną liczbę łączników nef, z wyjątkiem gwoździ przesuniętych o co najmniej d w poprzek włókien (EC5 - 8.3.1.1(8)).
Minimalna szerokość środnika:
bw,min = (nsz - 1)a2 +2a4c
Minimalny rozstaw gwoździ w poprzek włókien a2 wynosi 5d oraz minimalna odległość od boku nie obciążonego a4c wynosi także 5d (EC5 - tabl.8.2), stąd:
bw,min = 15d = 15x4,5 = 67,5 mm.
Przyjęto środnik o grubości bw = 100 mm
Przyjęte wymiary przekrojów elementów belki:
- półki 2 x 4,5x160 (PN-75/D-96000)
- środnik 100x200 (PN-75/D-96000)
Gwoździe 4,5/100 wbijane w dwóch szeregach dh = 10,5 mm.
4. Charakterystyka przekroju
Pole powierzchni:
- półki Af = 16,0x4,5 = 72,0 cm2
- środnika Aw = 20,0x10,0 = 200,0 cm2
Moment statyczny półki Sf:
z1 = (hf + hw)/2 = (4,5 + 20)/2 = 12,25 cm
Sf = Afxz1 = 72x12,25 = 882,0 cm3
![]()
![]()
5. Efektywne momenty bezwładności przekroju
Moduł podatności złączy w stanie granicznym użytkowalności (SGU) (tablica EC5 -7.1 - gwoździe osadzane bezpośrednio)
Kser = ρm1,5d0,81/30 = 4601,5x4,50,8/30 = 822,5 N/mm = 10,954 kN/cm
Moduł podatności złączy w stanie granicznym nośności (SGN)
Ku = 2/3Kser =2x8,225/3 = 7,302N/cm
Współczynnik redukcyjny w stanie granicznym użytkowalności:
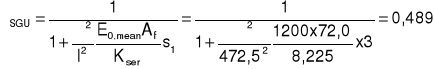
Efektywny moment bezwładności w stanie granicznym użytkowalności:
![]()
Współczynnik redukcyjny w stanie granicznym nośności:
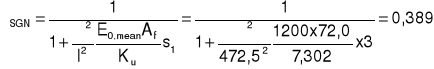
Efektywny moment bezwładności w stanie granicznym nośności:
![]()
6. Stan graniczny użytkowalności
Ugięcie końcowe belki (EC5 - 2.2.3(5)):
ufin = ufin,G + ufin,Q = uinst,G (1+kdef) +uinst,Q(1+ψ2,1kdef)
gdzie:
ufin - ugięcie końcowe,
uinst - ugięcie chwilowe,
kdef - współczynnik zależny od klasy użytkowania
ψ2,1 - wspołczynnik quasi-stałej wartości oddziaływania zmiennego ψ2,1 = 0,3 (EN0 - Tablica A.1.1)
Dla klasy użytkowania 1: kdef= 0,60 (EC5 -tabl. 3.2)
Ugięcia chwilowe (EC5 -NA.4) .
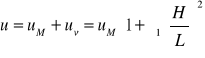
gdzie:
uM - ugięcie od momentu zginającego,
uV - ugięcie od siły poprzecznej,
H - całkowita wysokość przekroju
L - rozpiętość belki.
η1 - współczynnik wg Tablicy EC5 - NA 1.
Tablica NA.1 Współczynniki η1 do uwzględnienia wpływu sił poprzecznych
na ugięcia belek dwuteowych i skrzynkowych
Belki z drewna |
Belki z drewna I materiałów drewnopochodnych |
||||||
bw/bf'] |
1,00 |
0,50 |
0,33 |
0,25 |
0,33 |
0,25 |
0,125 |
η1 |
19,2 |
30,0 |
40,0 |
51,0 |
33,0 |
48,0 |
90,0 |
1) bw, bf - szerokości, odpowiednio: pasa i środnika |
|||||||
H = 2hf + hw = 2x4,5 + 20 = 29 cm.
L/h= 472,5/29 = 16,29 i bw/bf = b2/b1 = 0,625
![]()
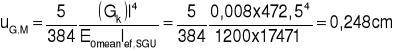
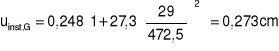
![]()
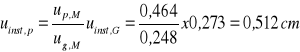
![]()
=
= 0,273(1+0,6) + 0,512(1+0,3x0,6) = 0,987cm
ulim = 472,5/300 = 1,575 cm > ufin
7. Stan graniczny nośności
7.1 Obciążenie łączników
Należy sprawdzić warunek (wg EC5 - B5) :
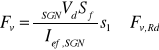
Wytrzymałość charakterystyczna na docisk gwoździa do drewna (gwoździe bez nawierconych otworów) (EC5 - 8.3.1.1(5)):
fh,1,k =fh,2,k = 0,082ρkd-0,3 = 0,082x380x4,5-0,3 = 19,84 MPa = 1,984 kN/cm2
Charakterystyczny moment uplastycznienia łącznika (EC5 - 8.3.1.1(4)):
My,Rk = 0,3fud2,6 = 0,3x 600x4,52,6 = 8988 Nmm = 0,899 kNcm
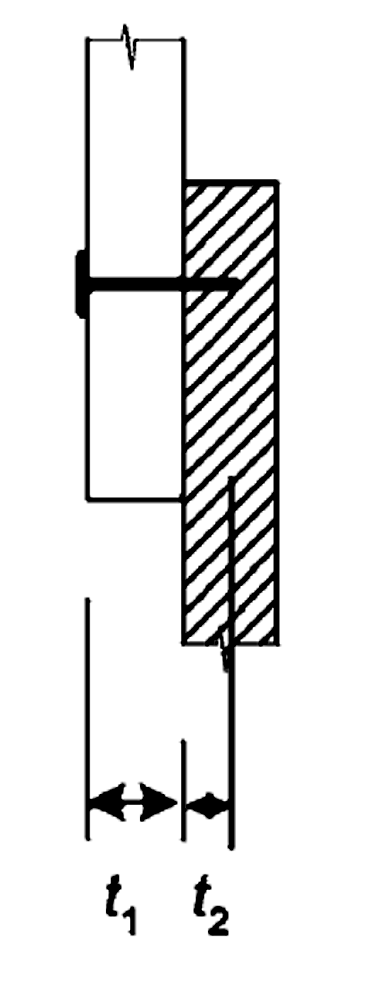
Złącze jednocięte (EC - Rys. 8.4a)
Nośność charakterystyczną gwoździ przy obciążeniu poprzecznym wyznaczono ze wzorów 8.6a - 8.6f (EC5). Nośności gwoździ odpowiadające wzorom 8.6a i 8.6b oraz wartości pierwszego składnika wzorów 8.6c - 8.6f, odpowiadającego teorii Johansena, wyznaczono podstawiając:
t1 = hf= 4,5 cm; t2= lpen = l - t - 1mm = 100 - 45 -1= 54 mm = 5,4 cm d=0,45cm; β = 1 oraz wyznaczone wyżej wartości fh,k = fh,1,k = fh,2,k i My,k.
Drugi składnik wzorów 8.6 c-f wyraża udział w nośności efektu liny, co pozwala uwzględnienie części nośności gwoździa na wyciąganie Fax,Rk. Udział efektu liny w przypadku gwoździ okrągłych jest ograniczony do 15 % części odpowiadającej teorii Johansena. (EC5 - 8.2.2(2)).
Nośność gwoździ wg teorii Johansena:
![]()
Fv,Rk,b =FJ,v,Rk,b = fh,2,kt2d = 1,984x5,4x0,45 = 4,822 kN
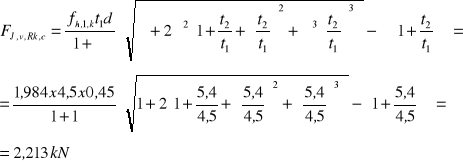
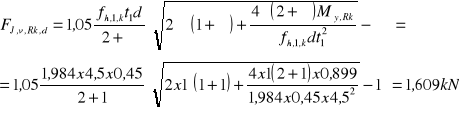
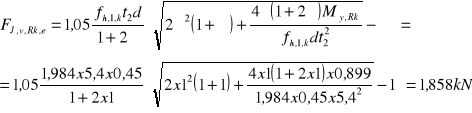
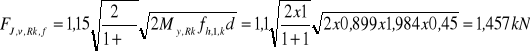
Nośność charakterystyczną gwoździ gładkich na wyciąganie Fax,Rk wyznacza się ze wzoru (EC5 wz.8.24):
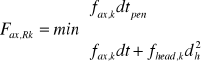
tpen = 5,4 cm, t = hf = 4,5 cm, dh = 10,5 mm = 1,05 cm.
![]()
(EC5 wz.8.25)
![]()
(EC5 wz.8.26)
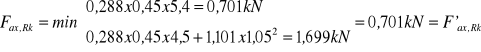
W przypadku długości zakotwienia gwoździ gładkich mniejszej niż12d nośność gwoździa na wyciąganie należy pomnożyć przez (tpen/4d - 2) (EC5 - 8.3.2(7)).
W tym przypadku: tpen/d = 5,4/0,45 = 12 , stąd: ![]()
Ostatecznie:
1/4xFax,Rk = 0,25x0,701 = 0,176 kN
Minimalna wartość części nośności charakterystycznej gwoździ wg teorii Johansena wynosi Fj,v,Rk,f = 1,457 kN.
Dopuszczalny 15 % udział nośności na wyciąganie
0,15x Fi,v,Rk,f = 0,15x1,457 = 0,224kN > 0,176 kN.
Nośność charakterystyczna gwoździa jest minimalną wartością ze wzorów:
![]()
![]()
![]()
![]()
![]()
![]()
Fv,Rk = 1,633 kN
Nośność obliczeniowa:
![]()
Obciążenie łącznika:
![]()
; ![]()
7.2 Naprężenia normalne
![]()
![]()
![]()
a) naprężenia w osi pasa rozciąganego:
![]()
b) naprężenia na zewnętrznej krawędzi półki:
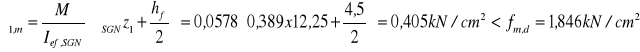
c) naprężenia na krawędzi środnika:
![]()
7.3 Maksymalne naprężenia ścinające
![]()
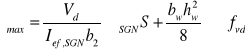
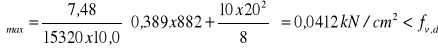
8. Docisk na podporach, liczba i rozmieszczenie łączników
![]()
Wyznaczenie długości oparcia belki przy założeniu równomiernego rozkładu naprężeń prostopadłych do włókien (docisku):
![]()
stąd: ![]()
Przyjęto konstrukcyjnie lop = 10 cm
Rzeczywista długość belki Lr:
Lr = l + 2lop = 450 + 2x10 = 470 cm
Lr = a1(nrz - 1) + 2a3tmin
gdzie:
nrz - liczba rzędów gwoździ
a1 = 6 cm a3tmin = (10 + 5cosα)d = 15d = 15x0,4,5 = 6,75 cm (EC5 - tabl. 8.2)
(a3t,max = 40d)
Maksymalna liczba rzędów gwoździ w belce:
![]()
Przyjęta liczba rzędów gwoździ: nrz = 77
Sprawdzenie odległości między skrajnymi łącznikami i końcem (czołem) belki:
![]()
Ponadto:
a2,min = 5d = 5x4,5 = 22,5 mm (EC5-tabl.8.2). Przyjęto a2 = 30 mm.
a4,c,min = 5,d = 5x4,5 = 22,5 mm (EC5-tabl.8.2). Przyjęto a4,c = 35 mm.
(a2 + 2a4,c = bw)
Łączna liczba gwoździ: 77x2x2 = 308.
Procentowe wykorzystanie granicznych wartości ugięć i nośności w zależności od wysokości środnika hw i rozstawu gwoździ a1
hw |
a1 |
SGN |
SGU |
||||
|
|
ufin/ulim |
Fv/Fv,Rd |
σ1t/ft,d |
σ1m/fm,d |
σ2m/fm,d |
τmax/fv,d |
cm |
% |
||||||
20 |
6 |
62,7 |
50,1 |
24,8 |
21,9 |
31,3 |
16,7 |
|
12 |
78,8 |
78,5 |
19,5 |
20,6 |
39,5 |
17,9 |
|
18 |
90,3 |
96,9 |
16,0 |
19,7 |
44,8 |
18,6 |
17,5 |
6 |
81,6 |
60,0 |
29,7 |
27,2 |
36,5 |
18,3 |
|
12 |
104,3 |
95,9 |
23,8 |
26,4 |
47,0 |
19,6 |
|
18 |
120,9 |
119,9 |
19,8 |
25,8 |
54,0 |
20,4 |
7
10
hf
z
y
bf
16
10
bw
hf
hw
4,5
4,5
20
z1=12,25