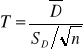
H0:μ1=μ2
test t-Studenta pozwala porównywać średnie w grupach niezależnych.
Test t-Studenta ma więcej wymagań, jest za to silniejszy i bardziej pożądany. Pierwszym wymaganiem jest względna normalność rozkładu zmiennej zależnej. Dlatego właśnie konieczne jest sprawdzenie rozkładu zmiennej w analizie częstości. Drugim założeniem testu Studenta jest założenie o równości wariancji. Innymi słowy - dwie porównywane grupy powinny być podobnie homogeniczne. Mówiąc po polsku - nie można porównywać dwóch grup, gdzie każda z nich jest badana innym testem, albo wtedy, gdy w jednej grupie występują wyniki bardzo skrajne (bardzo wysokie lub bardzo niskie), a w drugiej bardzo przeciętne. Jest to założenie ważne, choć niekonieczne - test t-Studenta został tak poprawiony, że pozwala na poprawne wyliczenia nawet w takich sytuacjach.
Jeśli założenia testu t-Studenta będą spełnione, warto z niego skorzystać. Jest on „mocniejszy”, bardziej rzetelny, niż test U Manna-Whitneya.
Rozkład t-studenta jest bardziej precyzyjną wersją rozkładu normalnego.
Rozkład t- studenta charakteryzowany jest dodatkowo przez tzw. liczbę stopni swobody. Oznacza to, że rozkład ten (posiadając stałą średnią i odchylenie standardowe) jest bardziej spłaszczony dla niewielkiej liczby stopni swobody, zaś gdy liczba ta (df- degrees of freedom) przekracza 120 i dąży do nieskończoności, rozkład t-studenta upodabnia się do rozkładu normalnego. Przy niewielkich df wartości krytyczne rozkładu t- studenta są więc nieco wyższe niż dla rozkładu normalnego. Stąd oszacowny przedział ufności dla średniej będzie nieco szerszy- co przestaje dziwić, jeżeli uświadomimy sobie, że uwzględnia on błąd pochodzący z dwóch źródeł- oszacowania średniej i oszacowania odchylenia standardowego.
Wzory
Test t-Studenta dla zmiennych powiązanych
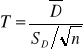
H0:μ1=μ2
Statystyka T ma rozkład t-Studenta gdzie
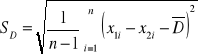
Liczba stopni swobody n1-1
![]()
jeżeli |T|< nie ma podstaw do odrzucenia hipotezy zerowej
jeżeli |T|≥ hipoteza zerowa jest odrzucona
Test t-Studenta dla zmiennych nie powiązanych
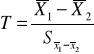
H0:μ1=μ2
Statystyka T ma rozkład t-Studenta gdzie
Liczba stopni swobody n1+n2-2

jeżeli |T|< nie ma podstaw do odrzucenia hipotezy zerowej
jeżeli |T|≥ hipoteza zerowa jest odrzucona
Dwie grupy pomiarów:
na tych samych podmiotach, np. przed i po posiłku (zmienne połączone)
na różnych podmiotach, np. ♀ i ♂ (zmienne niepołączone)
Zakładamy, że pomiary podlegają rozkładowi normalnemu.
Dla zmiennych niepołączonych dodatkowo zakładamy równość wariancji w grupach.
![]()
Hipoteza zerowa:
Hipotezy alternatywne
![]()
![]()
test jednostronny
test dwustronny
Czy dieta (np. sok grejpfrutowy) wpływa na DB? Y - wielkość będąca miarą DB.
![]()
![]()
![]()
Przeformułowanie problemu:
![]()
Wykonujemy eksperyment i wyznaczamy dla każdego osobnika Di.
Wyznaczamy estymaty (oszacowania) wartości oczekiwanej i odchylenia standardowego zmiennej losowej D
![]()
![]()
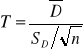
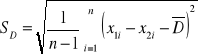
![]()
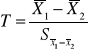
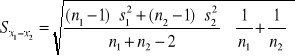
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()