LOGIKA Wykład IX 25.05.2002

Algebra zbiorów

Relacje

element a należy do zbioru A

element b nie należy do zbioru A

Pojęcie zawierania się zbioru w zbiorze

Mówimy, że zbiór A zawiera się w zbiorze B wtedy i tylko wtedy, kiedy każdy element zbioru A jest jednocześnie elementem zbioru B.

Zawieranie właściwe

Dwa zbiory są równe wtedy i tylko wtedy, kiedy mają takie same elementy.

- w logice te dwa zbiory są równe

- te same elementy nie są brane pod uwagę podwójnie

- kolejność nie gra roli

Twierdzenie o stosunkach zakresowych pomiędzy zbiorami

1. 
   

2. 
   

3. 
   

4. 
   

5. 
   

X - zmienna

p(x) - forma zdaniowa

zbiór wyznaczony przez formę zdaniową p(x)

Zbiór A, wyznaczony przez formę zdaniową p(x) jest to zbiór wszystkich przedmiotów spełniających formę zdaniową p(x).

Przykłady:

Zadanie I

Określić przy pomocy symbolu abstrakcji oraz wyznaczyć elementy zbioru wyznaczonego przez nierówność:

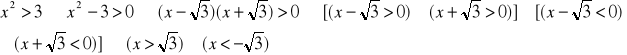
Zadanie II

Wymienić wszystkie elementy zbioru określonego następująco:

- te liczby dzielą 24 bez reszty

Zbiór pełny - oznaczamy 1

Działania na zbiorach

Zbiór Z jest sumą zbiorów X i Y wtedy i tylko wtedy, kiedy każdy element zbioru Z należy do zbioru X lub należy do zbioru Y.

Zbiór Z jest iloczynem (przekrój) zbiorów X i Y wtedy i tylko wtedy, kiedy każdy element zbioru X jest jednocześnie elementem zbioru Y.

Zbiór Z jest różnicą zbiorów X i Y wtedy i tylko wtedy, kiedy każdy element zbioru Z należy do zbioru X i nie należy do zbioru Y.

Zbiór Z stanowi różnicę symetryczną zbiorów X i Y wtedy i tylko wtedy, kiedy każdy element zbioru Z należy do zbioru X lub należy do zbioru Y, ale nie należy do obu zbiorów jednocześnie.

Zbiór X' jest dopełnieniem zbioru X wtedy i tylko wtedy, kiedy każdy element zbioru X' nie należy do zbioru X.

Zadanie III

Dane są dwa zbiory:

Obliczyć:

• sumę

• różnicę

• iloczyn

• dopełnienie

1=

Zadanie IV

A

B

A=B

a∈A

A

B

C

Zbiór pusty

C

A

B

D

1

A

B

A

B

A

B

X

1

X'

---