Zagadnienie 22: Podać algorytm wyznaczania pojemności linii dwuprzewodowej.
Jakim wzorem wyraża się potencjał elektryczny w punkcie P(x,y) pochodzący od dwóch równoległych, naładowanych przewodników nieskończenie długich i nieskończenie cienkich o stałej liniowej gęstości ładunku λ (różnoimienny ładunek na obu przewodnikach)?
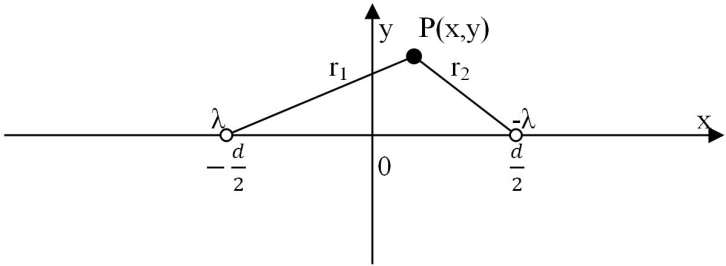
.
.
.
.Pojemność linii dwuprzewodowej nie zależy od:
przenikalności elektrycznej ośrodka, w jakim znajduje się linia.
potencjału pomiędzy przewodami.
ładunku znajdującego się na każdej z dwóch linii.
geometrii linii.
Przy obliczaniu pojemności linii dwuprzewodowej kolejność wykonywanych działań jest następująca:
przyjmujemy, że potencjał jednej z linii jest równy 0, ponieważ interesuje nas nie wartość samego potencjału jak różnica potencjałów pomiędzy liniami; dzięki temu założeniu możemy obliczyć różnicę potencjałów, która równa jest po prostu potencjałowi na „drugiej” linii; licząc pojemność jednostkową linii podstawiamy dane do wzoru:
, gdzie C - pojemność, l - jednostka długości układu, Q - ładunek zawarty na „drugiej” z linii, V2 - potencjał „drugiej” linii.obliczamy potencjał jako superpozycję potencjałów pochodzących od obu osi oraz różnicę potencjałów (napięcie) pomiędzy liniami; przyjmujemy, że gęstość liniowa ładunku na obu liniach jest równa co do wartości lecz przeciwnego znaku; przy obliczaniu pojemności musimy wziąć pod uwagę fakt, że przedstawiamy pojemność układu na jednostkę długości, więc nasz wzór przyjmuje postać:
, gdzie C - pojemność, l - jednostka długości układu, λ - gęstość liniowa ładunku, U - napięcie pomiędzy liniami.obliczamy różnicę potencjałów pomiędzy liniami ze wzoru:
; co stanowi napięcie pomiędzy liniami; ze wzoru:
, gdzie C - pojemność, l - jednostka długości układu, λ - gęstość liniowa ładunku, rA - odległość punktu, w którym wyznaczamy potencjał od pierwszej linii, rA - odległość punktu, w którym wyznaczamy potencjał od drugiej linii, ε - przenikalność elektryczna ośrodka.zarówno odpowiedzi a) i b) są prawidłowe.
Linie ekwipotencjalne w przypadku linii dwuprzewodowej stanowią:
okręgi, których osie geometryczne przewodów pokrywają się z „osiami elektrycznymi”.
hiperbole przesunięte względem siebie o wartość bezwzględną różnicy promieni przewodów.
okręgi, których osie geometryczne przewodów nie pokrywają się z „osiami elektrycznymi”.
hiperbole zdążające do pionu w środku odległości między przewodami.
Zagadnienie 24: Wyznaczyć pojemność linii jednoprzewodowej zawieszonej nad ziemią wykorzystując do tego celu metodę odbić zwierciadlanych.
Stosując metodę odbić zwierciadlanych do wyznaczenia pojemności linii jednoprzewodowej zawieszonej nad ziemią powinniśmy:
stworzyć obraz przekroju linii, w taki sposób, aby powierzchnia ziemi stała się linią symetrii, a w obrazie przekroju linii założyć, że gęstość liniowa ładunku jest taka sama co do wartości jak w linii rzeczywistej.
stworzyć obraz przekroju linii, w taki sposób, aby powierzchnia ziemi stała się linią symetrii, a w obrazie przekroju linii założyć, że gęstość liniowa ładunku jest taka sama co do wartości jak w linii rzeczywistej, ale przeciwnego znaku.
przyjąć, że gęstość liniowa ładunku w linii jest stała, co pozwala na zredukowanie linii do pojedynczego ładunku, stworzyć obraz ładunku o równej wartości w taki sposób, aby powierzchnia ziemi stała się linią symetrii.
przyjąć, że gęstość liniowa ładunku w linii jest stała, co pozwala na zredukowanie linii do pojedynczego ładunku, stworzyć obraz ładunku o równej wartości, ale przeciwnego znaku, w taki sposób, aby powierzchnia ziemi stała się linią symetrii.
Przy obliczaniu pojemności linii jednoprzewodowej zawieszonej nad ziemią przyjmujemy, że:
linia symetrii (czyli linia powierzchni ziemi) jest linią o potencjale równym 0.
odbicie linii rzeczywistej zawiera gęstość liniową ładunku równą co do wartości gęstości liniowej linii rzeczywistej o tym samym znaku.
różnica potencjałów pomiędzy rzeczywistą linią a ziemią będzie równa różnicy potencjałów pomiędzy linią rzeczywistą a obrazem tej linii odbitym względem ziemi.
odpowiedzi a) i c) są prawidłowe.
Na poniższym rysunku przedstawiono linię dwuprzewodową. Jaki warunek musi być spełniony, aby wyznaczyć wzór opisujący linię ekwipotencjalną (V = const) danego układu?
.
, gdzie K jest pewną stałą.
.
.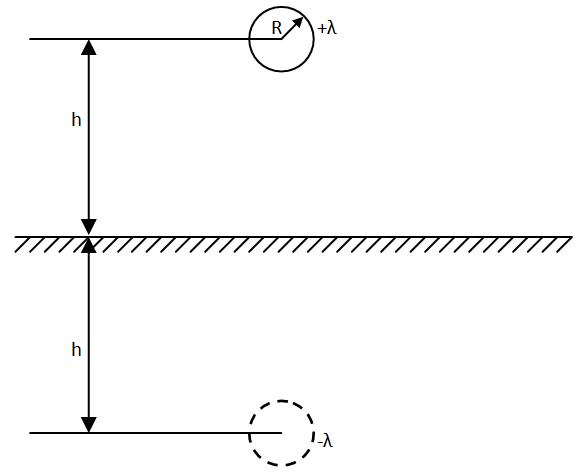
Ile wynosi pojemność jednostkowa linii jednoprzewodowej o promieniu R=0,025 [m] znajdującej się nad ziemią na wysokości h=12 [m], jeśli zastosujemy przybliżenie
?
Odpowiedzi:
c)
c)
b)
c)
b)
a)
b)
d)
Wyszukiwarka