Układy statyczne i astatyczne. Dokładność statyczna UAR

Weźmy pod uwagę liniowy układ zamknięty regulacji automatycznej złożony z obiektu o transmitancji operatorowej G_o(s) i regulatora o transmitancji operatorowej G_r(s) (rys.1).

Rys. 1. Schemat blokowy zamkniętego układu regulacji automatycznej

Pomiędzy transformatą E(s) uchybu regulacji e(t) i transformatą X_o(s) wielkości sterującej zachodzi zależność

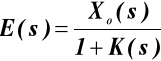
przy czym

K(s)=G_o(s)G_r(s)

jest transmitancją operatorową układu otwartego (transmitancja zwrotną).

Jak wiadomo między transformatą X(s) wielkości regulowanej x(t) i transformatą X_o (s) wielkości wartości zadanej x_o(t) zachodzi zależność

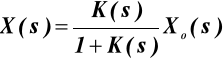
przy czym

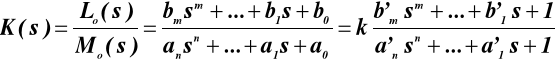
Układami statycznymi nazywamy układy bez członów całkujących, tzn. gdy transmitancja układu otwartego K(s) nie posiada biegunów zerowych (równanie M_o(s) nie posiada pierwiastków zerowych). Układy z członami całkującymi, gdy transmitancja układu otwartego K(s) posiada bieguny zerowe (równanie M_o(s) = 0 posiada pierwiastki zerowe) nazywamy układami astatycznymi. Rzędem astatyzmu układu nazywamy krotność bieguna zerowego transmitancji układu otwartego K(s) (krotność pierwiastka zerowego równania M_o(s)=0). Równanie M_o(s) = 0 ma μ(μ < n) pierwiastków zerowych, jeżeli a_o =0, a₁=0,...,a_μ-1 = 0 oraz a_μ ≠0. Układ jest więc układem astatycznym rzędu pierwszego, jeżeli a_o =0 oraz a₁≠ 0, odpowiednio rzędu drugiego, jeżeli a_o = 0, a₁ = 0 oraz a₂ ≠ 0 itd. Zakładamy przy tym, że równanie L_o(s) =0 nie posiada pierwiastków zerowych.

Dokładność statyczna układu regulacji - wyznaczanie uchybu ustalonego

Miarą dokładności w stanie ustalonym układu regulacji są wartości uchybu w stanie ustalonym (uchybu ustalonego, statycznego):

W ogólnym przypadku uchyb ustalony jest sumą dwóch składowych: składowej wywołanej zmianą wartości zadanej i składowej wywołanej zakłóceniami. Poszczególne składowe uchybu ustalonego wyznacza się z twierdzenia o wartości końcowej

W praktyce przy obliczaniu uchybów od wymuszenia wygodnie jest korzystać ze współczynników uchybu, będących współczynnikami stojącymi przy kolejnych potęgach operatora "s" w rozwiniętej w szereg MacLaurina transmitancji uchybowej przy Z(s)=0.

Współczynniki uchybowe Gk można obliczyć również z zależności:

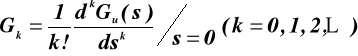
Decydujący wpływ na dokładność statyczną dla różnych typów sygnałów wymuszających ma postać transmitancji układu otwartego K(s) tzn. liczba jej zerowych biegunów i w konsekwencji rząd astatyzmu układu zamkniętego. Układ zamknięty jest układem astatycznym l-tego stopnia, jeżeli układ otwarty zawiera l- krotny biegun zerowy.

W tym przypadku wszystkie współczynniki uchybowe do
włącznie są równe zeru, tzn. układ astatyczny l-tego rzędu odtwarza dokładnie w stanie ustalonym tylko sygnały wymuszające x_o(t) dla których:

Np. dla wymuszenia w postaci skoku jednostkowego x_o (t)=1(t) i z(t)=0 mamy

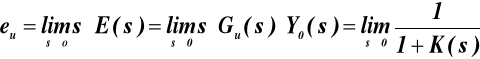
Z zależności tej wynika, że uchyb ustalony, dla wymuszenia w postaci skoku położenia (tzw. uchyb położeniowy) w układach statycznych, maleje wraz ze wzrostem współczynnika wzmocnienia układu otwartego z zależnością odwrotnie proporcjonalną, czyli:

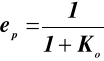
gdzie przez K0 oznaczono współczynnik wzmocnienia układu otwartego.

UWAGA !!!

Analogiczne obliczenia mogą być przeprowadzone dla innych sygnałów zewnętrznych np. zakłóceń.

E. Żak

Wykład

Podstawy automatyki - T. S.

3

---