Ćwiczenie 23
Temat: Wyznaczenie składowej poziomej indukcji pola magnetycznego Ziemi przy pomocy busoli statycznych
Wprowadzenie teoretyczne
Pole magnetyczne- jedna z form występowania pola elektromagnetycznego. Działa ono tylko na poruszające się cząstki i ciała, na przewodniki z prądem oraz na cząstki i ciała mające momenty magnetyczne.
Wytwarzane jest ono przez przewodniki z prądem, poruszające się naładowane elektrycznie cząstki i ciała, cząstki i ciała mające momenty magnetyczne, a także przez zmienne w czasie pole elektryczne. Charakteryzowane jest ono przez wektor indukcji pola magnetycznego B, oraz wektor natężenia pola H. Pole to jest polem bezźródłowym co wynika z faktu, że nie istnieją pojedyncze bieguny magnetyczne.
Z racji tej własności zachodzi:
![]()
Pole geomagnetyczne- pole magnetyczne Ziemi, które w każdym punkcie jest określone wektorem natężenia pola F. Bieguny magnetyczne cały czas zmieniają położenie. Oś symetrii pola magnetycznego nie pokrywa się z osią obrotu jest od niej odchylona o około 11o
Prawo Biota-Savarta- indukcja magnetyczna dB w próżni pola wytwarzanego przez mały element przewodnika o długości dl, przez który przepływa prąd o natężeniu I opisana jest wzorem:
![]()
r- wektor poprowadzony od elementu przewodnika do rozważanego punktu pola
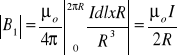
Zgodnie z tym prawem, całkowitą indukcję w środku geometrycznej kołowej, płaskiej pętli z prądem można wyrazić za pomocą wzoru:
I - natężenie prądu przepływającego przez pętlę, R - promień pętli.
Jeśli obwód składa się z n identycznych pętli to wówczas całkowita indukcja B=nB1.
Wartość składowej poziomej wektora indukcji ziemskiego pola magnetycznego zależy od wartości kąta i wartości indukcji pola wytworzonego przez pętlę z prądem. Kąt ten powstaje z odchylenia się igły busoli od kierunku północy w skutek dodatkowego działania indukcji pola magnetycznego pochodzącego od pętli z prądem.
Igła kompasu umieszczona jest w ziemskim polu magnetycznym, o składowej poziomej indukcji Bp, oraz w obszarze działania wektora indukcji pochodzącego od pętli z prądem. Wektor tej indukcji oznaczamy jako B⊥. Tak więc indukcja wypadkowa pola magnetycznego w tym wypadku wynosi B= B⊥+Bp. Gdy B⊥ jest równe zeru to oś igły pokrywa się z kierunkiem Bp. Natomiast gdy B⊥ jest różne od zera to igła ustawi się pod kątem α względem kierunku Bp. O wartości tego kąta decyduje warunek równoważenia się momentów sił pochodzących od tych pól. Za tp oznaczmy moment siły wytworzony przez Bp natomiast za t⊥ moment siły wytworzony przez B⊥. Równowaga ma więc postać:
tp=- t⊥ μxBp= -μxB⊥ μ - moment magnetyczny igły kompasu
Otrzymujemy dalej wartości:
![]()
μBpsinα= μB⊥cosα ostatecznie otrzymujemy:
Dzięki temu wzorowi możemy obliczyć wartość składowej poziomej indukcji pola magnetycznego Ziemi.
Natężenie pola magnetycznego (H) - wielkość wektorowa charakteryzująca pole magnetyczne w próżni. W ustalonym punkcie przestrzeni wartość liczbowa natężenia pola pochodząca od elementu przewodnika dl, przez który płynie prąd o natężeniu I jest określona wzorem:
![]()
r- wektor poprowadzony od elementu przewodnika do rozważanego punktu pola
J- polaryzacja magnetyczna ośrodka
Wektor indukcji magnetycznej (B) - stanowi siłową charakterystykę pola magnetycznego. Wektor ten możemy wyliczyć na jeden z trzech równoważnych sposobów, na podstawie siłowego działania pola magnetycznego na :
Poruszający się w nim punktowy ładunek próbny
Mały element przewodnika z prądem
Niewielką ramkę z prądem
![]()
Siła Lorenza z niej możemy wyliczyć wartość indukcji
Dla większości substancji (oprócz ferromagnetyków) i niezbyt silnych pól zależność B od H jest liniowa i wyraża się wzorem:
![]()
Gdzie: H- natężenie pola magnetycznego
μ0- przenikalność magnetyczna próżni
μr- przenikalność magnetyczna ośrodka
Magnetyczny moment dipolowy (μm.): wielkość wektorowa, która charakteryzuje rozkład prądów elektrycznych lub ciał magnesowanych. Wyznacza się on wzorem:
![]()
Gdzie: N- ilość płaskich obwodów
Ii- natężenie prądu płynącego przez i-ty obwód
Si- powierzchnia tego obwodu
ni- wektor normalny do tej powierzchni
Znajomość magnetycznego momentu dipolowego umożliwia wyznaczenie pola elektromagnetycznego w dużych odległościach od układu prądów.
Magnetyczny moment dipolowy magnesu sztabkowego wynosi:![]()
Gdzie: J- wektor polaryzacji magnetycznej
V- objętość magnesu
Wektor μm. jest skierowany od bieguna południowego do północnego.
W opisie mikroskopowym w substancji znajdującej się w polu magnetycznym o natężeniu H ulegają uporządkowaniu dipole magnetyczne (cząstki, atomy, czy też układy atomów z wyróżnionym biegunem północnym i południowym), wskutek czego pojawia się wypadkowa polaryzacja opisana wektorem polaryzacji J (będąca momentem magnetycznym na jednostkę objętości) B=μoH+J
Moment siły - określa działanie obrotowe siły. Jest to wielkość fizyczna wektorowa równa iloczynowi wektorowemu wektora położenia r punktu, w którym jest zaczepiona siła F i tej siły M = r x F. M z własności iloczynu skalarnego jest wektorem prostopadłym do r jak i do F (prostopadły do płaszczyzny wyznaczonej przez wektory r i F).
1 Tesla - jednostka indukcji magnetycznej określona jako indukcja pola magnetyczna pola magnetycznego jednorodnego przy, której na przekrój poprzeczny 1 m2 przypada strumień magnetyczny 1 Wb (1 weber strumień indukcji magnetycznej).
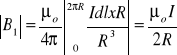
![]()
Wyszukiwarka