Laboratorium Fizyki I |
Ćwiczenie nr: 38 |
|||
|
Data: 23.11.2005 |
|||
Wydział: MCHTR
|
Grupa: 23 |
Zespół: 8 |
Punktacja |
Przygotowanie: 3,5 |
Nazwisko i imię: Fiodorow Michał
|
|
|
||
Temat ćwiczenia: Badanie zjawiska skręcenia płaszczyzny polaryzacji światła. |
|
Sprawozdanie: |
||
Prowadzący: M.Ćwil |
|
Suma punktów: |
||
1. Wiadomości wstępne:
POLARYZACJA ŚWIATŁA, (enc. PWN) całkowite lub częściowe uporządkowanie drgań fali świetlnej; może zachodzić: przy odbiciu na granicy 2 ośr. (w szczególnym wypadku przy kącie padania równym kątowi Brewstera światło odbite jest całkowicie spolaryzowane liniowo), przy rozchodzeniu się światła w ośr. anizotropowych, przy rozpraszaniu światła (światło obserwowane pod kątem prostym do kierunku padania wiązki jest całkowicie spolaryzowane); do liniowej polaryzacji światła stosuje się np. polaroidy, a do polaryzacji światła kołowej i eliptycznej — np. polaroidy z ćwierćfalówkami; liniową polaryzację światła odkrył 1808 fr. fizyk É.L. Malus, kołową i eliptyczną — 1822 fr. fizyk A.J. Fresnel.
2. Przebieg ćwiczenia i jego cel.
Celem wykonywanego przez nas ćwiczenia było poza zapoznaniem się z urządzeniem do badania skręcania płaszczyzn polaryzacji, zbadanie kąta skręcania płaszczyzn promienia świetlnego przechodzącego przez ciało aktywne optycznie, którym w naszym przypadku był roztwór cukru w wodzie destylowanej.
Kolejnym etapem było wyznaczenie zdolności skręcającej roztworu a następnie wyznaczenie stałej Verdeta oraz wyznaczenie ilorazu e/me.
Na początek musieliśmy ustawić polarymetr, wykorzystując fakt, że dla czystej wody kąt skręcenia powinien wynosić 0. Potem przygotowaliśmy roztwory wody destylowanej i cukru o takich proporcjach, że na 50 ml (czyli 50g) wody przypadały kolejne wartości wagi cukru podane w tabeli poniżej. Mieszając kolejne roztwory umieszczaliśmy je po kolei w pojemniku i mierzyliśmy kat skręcenia. Stężenie roztworu określa następujący wzór:
![]()
mr - masa rozpuszczalnika (50ml = 50g)
|
Ilość cukru- ms [g] |
kąt skręcenia [ ° ] |
[ ° ] |
[rad] |
Stężenie- c [%] |
1. |
1 |
14,00 |
3,00 |
0,052352 |
1,96 |
2. |
2 |
15,00 |
4,00 |
0,069802 |
3,85 |
3. |
3 |
16,40 |
5,40 |
0,094233 |
5,66 |
4. |
4 |
18,45 |
7,45 |
0,130007 |
7,41 |
5. |
5 |
20,20 |
9,20 |
0,160545 |
9,09 |
6. |
6 |
21,85 |
10,85 |
0,189339 |
10,71 |
7. |
7,2 |
24,85 |
13,85 |
0,24169 |
ok. 12,5 |
|
0 |
11,00 |
0 |
0 |
0 |
Skręcenie właściwe:
* = (16,17·10-3 )/(1493,5·10-3) = 0,0108 [rad]
Błąd przypadkowy skręcenia właściwego:
Mnożymy błąd wyliczony przez program „Origin” przez współczynnik t-Studenta t=4,03
** = 0,00097528·4,03 = 0,00393 = 4·10-3
Błąd systematyczny skręcenia właściwego:
![]()
Ponieważ ![]()
, więc najpierw obliczamy *C:
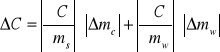
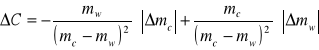
![]()
![]()
Długość kuwety z roztworem: h = 149,35 ± 0,05 [mm] = 0,14935 ± 0,00005 [m]
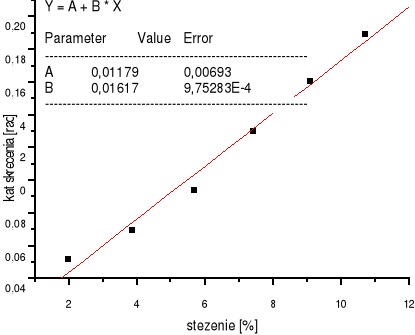
Współczynnik kierunkowy nachylenia prostej y = a + b·x :
b = 0,01617
* = *·h·c b=·h = b/h
Błąd liczymy dla każdego z pomiarów i wyliczamy średnią. I tak po kolei błąd Δ C wynosi:
1. 0,02 2. 0,018839 3. 0,017751 4. 0,016732 5. 0,015775 6. 0,014876 7. 0,014031, co daje średnio: Δ C = 0,0168577 = 0,017
Obliczamy :
![]()
![]()
![]()
![]()
Ponieważ wielkości C, były mierzone wielokrotnie (różne wartości) należy policzyć błąd systematyczny dla każdego pomiaru według powyższego wzoru, a następnie uśrednić go (dla obliczenia przyjmujemy jednostki C [1] a nie [%] - należy wartość C podzielić przez 100). Ponieważ dla pierwszego pomiaru otrzymalibyśmy dzielenie przez 0, błąd liczymy dla pomiarów 2-7
Lp. |
Δ |
1 |
0,015719 |
2 |
0,007949 |
3 |
0,005439 |
4 |
0,004184 |
5 |
0,003414 |
6 |
0,002899 |
7 |
0,015719 |
Wynik uśredniony: Δ = 0,006601 = 0,007 [rad]
( ± Δ ) = (0,011 ± 0,007) [rad]
Obliczenie nieznanego stężenia Cx:
= ·h·Cx Cx = /(·h)
Cx = 0,24169/(0,011·1,4935) = 14,71 [%]
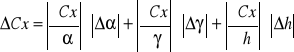
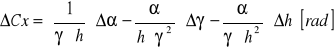
![]()
![]()
![]()
Cx = 0,76 [%]
Cx = 14,71 ± 0,76 [%]
Różnica współczynników załamania fali spolaryzowanej prawo i lewoskrętnie w funkcji stężenia:
Lp. |
C [%] |
n [x10-9] |
1 |
0 |
0 |
2 |
1,96 |
179 |
3 |
3,85 |
241 |
4 |
5,66 |
383 |
5 |
7,41 |
554 |
6 |
9,09 |
635 |
7 |
10,7 |
683 |
![]()
, gdzie k - liczba falowa
![]()
Aktywność optyczna wywołana polem magnetycznym
|
Natężenie prądu |
kąt skręcenia |
|
|
indukcja B |
|
[A] |
[ ° ] |
[ ° ] |
[rad] |
[T] |
|
0 |
117,35 |
0 |
0 |
0 |
1. |
1 |
113,65 |
-3,70 |
-0,06457 |
0,017144 |
2. |
2 |
111,05 |
-6,30 |
-0,10994 |
0,034289 |
3. |
3 |
108,50 |
-8,85 |
-0,15444 |
0,051433 |
4. |
4 |
106,05 |
-11,30 |
-0,19719 |
0,068578 |
5. |
5 |
103,45 |
-13,90 |
-0,24256 |
0,085722 |
6. |
6 |
101,10 |
-16,25 |
-0,28357 |
0,102866 |
Do pomiaru prądu w cewce użyto amperomierza analogowego klasy 0,5 na zakresie 6A w związku z czym ∆I = 0,03 A.
Indukcję magnetyczną wyznaczyłem ze wzoru: ![]()
, gdzie:
μ0 = 4*π*10-7 [H/m] (przenikalność magnetyczna próżni),
N = 4200zw. (ilość zwojów cewki),
L = 0,28 ± 0,001 m (długość cewki),
K = 0,91 (wsp. uwzględniający skończone rozmiary solenoidu)
a jej błąd korzystając z metody różniczki zupełnej:
![]()
![]()
0,0009 [T]
Stałą Verdeta obliczono ze wzoru: ![]()
b = (2,48661 ± 0,07104) rad/T (wsp. nachylenia prostej α(B) )
h = (0,086 ± 0,0005) m (długość pręta)
![]()
= 28,914 [rad/m*T]
Błąd przypadkowy stałej Verdeta:
Mnożymy błąd wyliczony przez program „Origin” przez współczynnik t-Studenta t=4,03 (=0,99 (poziom ufności); k = n-r = 7-2 = 5 t(,k)):
V = 0,071·4,03 = 0,286 = 0,29
Błąd systematyczny liczę metodą różniczki zupełnej: ![]()
V = 1
Błąd systematyczny jest o rząd wielkości większy niż przypadkowy, więc jego użyję przy zapisywaniu wyniku
V = (28,9 ± 1) [rad/m*T]
W oparciu o obliczoną stałą Verdeta obliczamy wartość stosunku e/me
![]()
, a ![]()
![]()
λ1 = 546,1 nm n1 = 1,93322
λ2 = 587,3 nm n2 = 1,92286
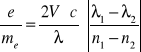
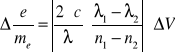
(długość fali światła sodowego wynosi 589,3nm)
Wartość wyliczona: e/me = (1,170 ± 0,04)*1011 [C/kg]
Wartość teoretyczna: e/me = 1,759*1011 [C/kg]
3. Wnioski:
Pierwsza część ćwiczenia polegała na wyznaczeniu zdolności skręcającej roztworu. Stosunkowo duży błąd spowodowany był trudnością znalezienia położenia półcienia. Szczególnie widać to dla środkowych pomiarów pierwszego ćwiczenia (trzeba tu dodać że pomiary przeprowadzone były z jedną pękniętą szybką kuwety).
Roztwór wody destylowanej z cukrem skręca płaszczyznę polaryzacji w prawo, stąd nazywamy go prawoskrętnym.
Stężenie nieznane wynosi 14,76 ± 0,76%.
Kąt skręcenia płaszczyzny polaryzacji dla ciężkiego flinta jest w lewą stronę więc materiał badany nazywamy lewoskrętnym albo ujemnym. Wartość wyliczona stosunku e do me z wartością teoretyczną nie pokrywają się.
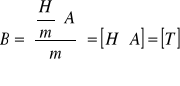
Wyszukiwarka