KATARZYNA STANOCH
MAŁGORZATA WOLAS
GR I
Kolegium Nauczycielskie
Bielsko-Biała
Ul. Krakowska 30
Ćwiczenie nr 75
WYZNACZANIE OGNISKOWEJ SOCZEWKI ROZPRASZAJĄCEJ
I ZWIERCIADŁA WYPUKŁEGO METODĄ OBRAZÓW POZORNYCH.
1 -
Soczewki rozpraszające i sferyczne zwierciadła wypukłe dają wyłącznie obrazy pozorne, których nie możemy obserwować na ekranie.
Związek między odległością przedmiotu i obrazu pozornego od soczewki oraz ogniskową soczewki, podobnie jak związek między odległością przedmiotu i obrazu od zwierciadła dany jest wzorem:
gdzie: x, y - odległość odpowiednio przedmiotu i obrazu od soczewki (zwierciadła)
Pomiar odległości y można dokonać w układzie przedstawionym na rysunku I
i II, z którego widać, że:
y = n - l
RYSUNEK I (dla soczewki)
gdzie: S-soczewka
P-płytka
F-ognisko
- 2 -
RYSUNEK II (dla zwierciadła wypukłego)
gdzie: Z-zwierciadło
P-płytka
Bieg promieniu w układach pomiarowych do wyznaczania ogniskowej f soczewki rozpraszającej i zwierciadła wypukłego przedstawiono odpowiednio na rysunku I i II. Dla obu układów ogniskowa f dana jest wzorem:
gdzie: l-odległość pomiędzy płytką a soczewką lub zwierciadłem
n- odległość pomiędzy płytką a obrazem A2B2
- 3 -
OBLICZENIA:
|
lp [cm] |
lpł [cm] |
ls; lz [cm] |
loi [cm] |
lo [cm] |
|||
soczewka |
20 |
60 |
40 |
75 |
80 |
90 |
95 |
85 |
zwierciadło |
20 |
70 |
90 |
46 |
50 |
40 |
36 |
43 |
lp-położenie przedmiotu
lpł-położenie płytki
ls-położenie soczewki
lz-położenie zwierciadła
loi-położenie obrazu, ostrza
|
x [cm] |
Δx [cm] |
n [cm] |
Δn [cm] |
l [cm] |
Δl [cm] |
f [cm] |
Δf [cm] |
soczewka |
20 |
0,2 |
25 |
0,1 |
20 |
0,1 |
-6,7 |
0,4 |
zwierciadło |
70 |
0,2 |
27 |
0,1 |
20 |
0,1 |
-7,8 |
0,3 |
Korzystając ze wzoru: obliczamy ogniskową f badanego zwierciadła i soczewki, oraz błąd Δf, ze wzoru:
Przykład obliczania ogniskowej i błędu pomiaru dla soczewki i zwierciadła:
SOCZEWKA:
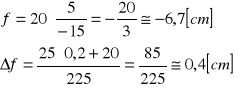
ZWIERCIADŁO:
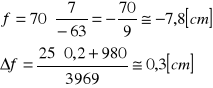
- 4 -
Średnia wartość ogniskowej soczewki rozpraszającej wynosi:
![]()
Średnia wartość ogniskowej zwierciadła wypukłego wynosi:
![]()
- 5 -
P
S
A2
B2
n
l
y
B1
A1
F
x
B
A
O
F
B1
A1
y
l
n
x
Z
P
B2
A2
B
A
Wyszukiwarka