Politechnika Śląska

Wydział AEiI

Kierunek AiR

Ćwiczenia laboratoryjne z fizyki :

Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła matematycznego i wahadła rewersyjnego.

Grupa I, sekcja 5

Tomasz Kotyczka

Krzysztof Czubin

Grzegorz Patoła

Gliwice 17.04.1997

1.Opis teoretyczny.

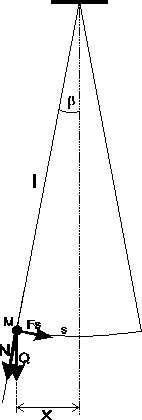
Wahadło matematyczne.

Wahadłem matematycznym nazywamy punkt materialny zawieszony na nieważkiej i nierozciągliwej nici umieszczony w polu siły ciężkości. Układ taki nie istnieje w rzeczywistości ale przybliżonym modelem wahadła matematycznego może być ciężkie ciało zawieszone na lekkiej nici , której długość jest znacznie większa od wymiarów tego ciała. Wahadło matematyczne wychylone z położenia równowagi o kąt a porusza się pod wpływem składowej Fs własnego ciężaru :

Ponieważ
, a dla małych wartości kąta b : x » s więc:

Fs jest więc w przybliżeniu proporcjonalne do s. Ruch punktu, w którym działająca na niego siła jest skierowana wzdłuż tej samej prostej w kierunku jakiegoś stałego punktu i wartość tej siły jest proporcjonalna do odległości między tymi punktami, nazywamy ruchem drgającym prostym lub harmonicznym.

W rozpatrywanym przypadku ruch punktu M jest tylko w przybliżeniu harmoniczny, ponieważ punkt porusza się po łuku, nie zaś po jego cięciwie i przyspieszenie jego nie jest ściśle proporcjonalne do wychylenia. Mimo to można rozważać ten ruch jako harmoniczny dla niewielkich wychyleń.

Z rozwiązania równania różniczkowego drgań harmonicznych mamy :

w przypadku wahadła matematycznego :
z czego wyliczamy

gdzie : g - szukane przyspieszenie ziemskie

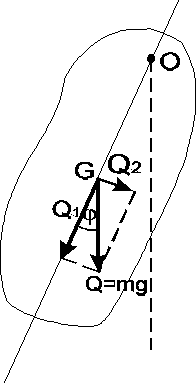
Wahadło rewersyjne.

Wahadłem fizycznym nazywamy każdą bryłę sztywną wahającą się pod wpływem siły ciężkości dokoła osi, nie przechodzącej przez środek masy tej bryły. Wypadkowa sił ciężkości działających na ciało równa się ciężarowi wahadła Q = mg, punktem przyłożenia tej wypadkowej jest środek ciężkości wahadła G. Zgodnie z zasadą d'Alemberta równanie ruchu ma postać :

gdzie J - moment bezwładności wahadła względem osi O

a - odległość środka ciężkości G od osi obrotu O

Jest to równanie ruchu wahadła fizycznego.

Jeżeli wychylenie j jest małe to sin(j) » j. Wziąwszy pod uwagę to zastrzeżenie, możemy napisać poprzednie równanie w następującej postaci:

Jest to równanie ruchu drgającego harmonicznego.

Rozwiązanie tego równania jest następujące :

jo jest amplitudą ruchu, czyli największym odchyleniem kątowym punktu materialnego od jego położenia równowagi, y jest fazą początkową ruchu.

Przyspieszenie kątowe tego ruchu wynosi :

Z równania drgań harmonicznych mamy:

Porównując i przekształcając powyższe równania otrzymujemy wzór na okres wahań :

Aby powiązać T z wymiarami geometrycznymi wahadła posłużymy się twierdzeniem Steinera:
JG jest momentem bezwładności względem osi przechodzącej przez jego środek ciężkości i równoległej do osi zawieszenia O. Wartość JG możemy zapisać w postaci :
, k - ramię bezwładności siły. Wobec tego :
. Po wstawieniu do wzoru na okres wahań mamy:

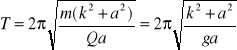
gdzie
nazywamy długością zredukowaną wahadła (jest to długość odpowiadającego wahadła matematycznego o tym samym okresie drgań). Ze wzoru wynika, że ten sam okres drgań mają wahadła o tej samej długości l niezależnie od wartości a, po przekształceniu mamy :
z czego widać, że istnieją dwie takie wartości a dla których wahadło ma ten sam okres wahań. Odległość dwóch takich punktów położonych po przeciwnych stronach środka ciężkości w odstępach nierównych, nazywamy właśnie długością zredukowaną wahadła: l = a+a'

Wahadło rewersyjne (Katera)

Jest to wahadło rewersyjne, w którym położenia osi zawieszenia są stałe. Składa się ono z metalowej sztaby, wzdłuż której można przesuwać dwie masy o kształcie soczewek (kształt ten ma na celu zmniejszenie oporu powietrza w czasie ruchu).Na sztabie znajdują się dwa ostrza, które są osiami wahań wahadła. Jedno z ostrzy znajduje się pomiędzy masami drugie na zewnątrz ich. Długość zredukowana wahadła rewersyjnego jest to odległość między środkami ciężkości mas wtedy gdy okresy drgań są identyczne dla obu położeń wahadła.

2. Opis ćwiczenia

W pierwszej części ćwiczenia przyspieszenie ziemskie było wyznaczane przy pomocy wahadła matematycznego. Pomiar polegał na mierzeniu czasu 20 wahnięć( w celu zmniejszenia błędu pomiaru czasu trwania jednego okresu) wahadła dla każdej długości wahadła w zakresie 20¸ 40 cm co 2 cm Wartość g można wyliczyć ze wzoru który jest przekształceniem wzoru na okres drgań wahadła matematycznego:

Przy kilku pomiarach dokonanych dla różnych długości wahadła można też zastosować metodę Bessela eliminującą część błędów związanych z pomiarem długości wahadła :

gdzie d - jest różnicą długości wahadła o okresach wahań T1 i T2.

W drugiej części ćwiczenia g było wyznaczane na podstawie okresu drgań wahadła rewersyjnego. Najpierw należało wyznaczyć długość zredukowaną wahadła. W tym celu były dokonywane pomiary czasu trwania 10 okresów wahnięć wahadła zawieszanego na ostrzu A i następnie na ostrzu B, dla różnych odległości mas od siebie zmienianych co 50 mm. Następnie został sporządzony wykres zależności okresu drgań wahadła od odległości mas. Z tego wykresu w punkcie przecięcia wykresów dla osi zawieszenia A i B została odczytana długość zredukowana wahadła, po czym został przeprowadzony pomiar czasu trwania 50 okresów dla tej długości na obu ostrzach, oraz dla długości sąsiadujących (w celu sprawdzenia dokładności wyznaczenia długości zredukowanej). W końcu zostały wykonane obliczenia :

Okres średni dla długości zredukowanej:

Przyspieszenie ziemskie :

3. Tabela pomiarowa.

Wahadło matematyczne.

liczba mierzonych okresów n = 20

Lp.	Długość l [cm]	czas t [s]	okres T [s]
1	24	19,869	0,99345
2	26	20,664	1,0332
3	28	21,496	1,0748
4	30	22,165	1,1082
5	32	22,875	1,1437
6	34	23,580	1,1790
7	36	24,221	1,2110
8	38	24,841	1,2420
9	40	25,566	1,2783
10	42	26,175	1,3087
11	44	26,774	1,3387
12	46	27,338	1,3669
13	48	27,949	1,3974
14	50	28,489	1,4244

Wahadło rewersyjne.

liczba mierzonych okresów n = 5

Położenie x	Ostrze A		Ostrze B
[mm]	czas t [s]	okres T [s]	czas t [s]	okres T [s]
30	6,562	1,3124	6,659	1,3318
50	6,472	1,2944	6,533	1,3066
70	6,399	1,2798	6,418	1,2836
90	6,340	1,2680	6,301	1,2602
110	6,292	1,2584	6,195	1,2390
130	6,264	1,2528	6,102	1,2204
150	6,236	1,2472	5,984	1,1908
170	6,221	1,2442	5,887	1,1774
190	6,217	1,2434	5,811	1,1622
210	6,220	1,2440	5,753	1,1506
230	6,235	1,2470	5,736	1,1472
250	6,252	1,2504	5,726	1,1452
270	6,280	1,2560	5,786	1,1572
290	6,313	1,2626	5,911	1,1822
310	6,353	1,2706	6,150	1,2300
330	6,397	1,2794	6,627	1,3254
350	6,443	1,2886	7,331	1,4662
370	6,498	1,2996	8,786	4,3930

Pomiary dokonane po wyznaczeniu l = 382 mm

n = 50

Położenie x	Ostrze A		Ostrze B
[mm]	czas t [s]	okres T [s]	czas t [s]	okres T [s]
90	63.371	1.26800	63.023	1.26400
80	63.642	1.27284	63.598	1.27196
75	63.841	1.27682	63,920	1.27840

4.Opracowanie wyników pomiarów.

Przyśpieszenia ziemskiego za pomocą wahadła matematycznego

i i oraz

to:

korzystając z regresji liniowej obliczmy a

a=4,0117

oraz korzystając z w/w zależności obliczmy g

g=9,840

Błędy przyjęte w obliczeniach:

Dla elektronicznych mierników cyfrowych błąd wynosi 0,5% wskazania

( błąd czasu Δt)

Błąd okresu wynosi więc ΔT=Δt/20.

Dl = 2 mm - pomiar był dokonywany "na oko" przy pomocy podziałki o działce elementarnej 1 mm .

Uwzględniając te błędy obliczamy maksymalne odchylenie współczynnika a.

Uwzględniając błędy otrzymujemy maksymalną wartość odchylenia współczynnika a

amax=4,052

korzystając z zależności:

mamy:

gmin=9,742

więc:

Δg=g - gmin = 0,098

Ostatecznie przyśpieszenie ziemskie wynosi

gsr = 9,840±0,098

Przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego:

Okres drgań spełniający warunek odwracalności wynosi:

To=1,272[s], l=382[mm]

g = 9,345

Błędy przyjęte w obliczeniach:

Błąd pomiaru długości Dl = 0.5 mm - mimo, że pomiar długości wahadła był dokonany przy pomocy suwmiarki rzeczywisty błąd pomiaru był większy ze względu na to, że szczęki suwmiarki nie przylegały dokładnie do ciężarków oraz ciężarki nie były umocowane całkowicie nieruchomo na osi wahadła.

Błąd pomiaru czasu jest taki jak dla wahadła matematycznego, przy czym

ΔT = Δt/50 = 0,0064s

Obliczenie błędu (z różniczki zupełnej:

Δg=0,106

Ostatecznie wartość przyśpieszenia ziemskiego:

5.Podsumowanie.

Jak wykazało doświadczenie wynik uzyskany przy pomocy wahadła matematycznego, czyli modelu mającego mniej wspólnego z rzeczywistością, wbrew pozorom dał wynik bliższy wartości tablicowej niż wynik uzyskany przy pomocy wahadła rewersyjnego. Przy założeniu, że obydwa pomiary były dokonane z podobną dokładnością przyczyną tego stanu może być zaniedbanie pewnych czynników zewnętrznych działających na wahadła oraz pewne przybliżenia w obliczeniach. Przybliżenie występujące w obliczeniach to zastąpienie sin(a) przez a, które daje o sobie znać przy większych kątach wychylenia wahadeł. Mogło to być jedną z przyczyn błędów (szczególnie, że wahadło rewersyjne przy pomiarze 50 okresów musiało być wychylone bardziej). Drugą przyczyną błędów były zapewne opory ruchu działające na wahadła. Opór związany z tarciem w miejscu zawieszenia był zapewne większy przy wahadle rewersyjnym choćby ze względu na jego masę. Drugi z oporów to opór powietrza. Przy wahadle rewersyjnym był ,on zapewne większy ze względu na większe rozmiary a co za tym idzie, większą powierzchnię czołową wahadła. Jak z tego wynika w rzeczywistych warunkach nie da się dokładnie wyznaczyć przyspieszenia ziemskiego nie uwzględniając wpływu otoczenia na użyte modele matematyczne.

---