1.WSTĘP TEORETYCZNY.

1.1 Cel ćwiczenia : zapoznanie z metodą pomiaru współczynnika przewodności cieplnej izolatorów oraz dokonanie tego pomiaru.

1.2 Wiadomości ogólne.

Jeżeli przeciwległe ścianki płyty o powierzchni przekroju S i grubości d1 mają odpowoednio temperatury T1 i T2 przy założeniu , że T1>T2 , to następuje przepływ ciepła w kierunku powierzchni o niższej temperaturze.

Ilość ciepła przepływającego w jednostce czasu w stanie stacjonarnym wyraża się wzorem :

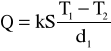
, w naszym przypadku :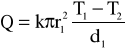

gdzie k - współczynnik przewodności cieplnej , który oznacza ilość ciepła przechodzącego w jednostce czasu przez jednostkę powierzchni przy jednostkowym gradiencie temperatury.

Różne ciała mają różne wartości przewodności cieplnej. Ciała o małej wartości współczynnika przewodności cieplnej ( 10-1-10-2 J/(msK) ) nazywają się izolatorami.

Aby wyznaczyć wspólczynnik przewodności cieplnej płytki , należy zmierzyć jej grubość d1 , promień r1 , temperatury T1 i T2 przeciwległych powierzchni oraz ilość ciepła Q przechodzącą w jednostce czasu między powierzchniami o tych temperaturach. Ta ilość ciepła jest bezpoścrednio trudna do zmierzenia , dlatego wyznacza się ją pośrednio metodą stygnięcia.

Jeżeli szybkość stygnięcia w pobliżu temperatury T2 jest n = T / t , to ilość wypromieniowanego ciepła w jednostce czasu jest równa m c n , gdzie c - ciepło wlaściwe płyty a m - masa płyty.

Zakładając , że ilość wypromieniowanego ciepła jest proporcjonalna do powierzchni , można wyrazić ilość ciepła wypromieniowaną przez jednostkę powierzchni w jednostce czasu jako :

Uwzględniwszy fakt , że po ustaleniu się temperatur ilość ciepła przewodzona przez badaną płytę jest równa ilości ciepła wypromieniowanej przez boczną i dolną powierzchnię płyty , możemy napisać :

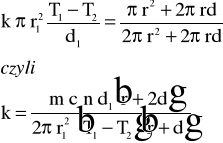
1.3 Przebieg doświadczenia.

Układ do wyznaczania przewodności cieplnej składa się z mosiężnej puszki o grubym dnie ( P1), płytki mosiężnej ( P2 ) , płytki badanej ( P ) , termostatu oraz cyfrowego miernika temperatury. Puszka , płytka badana i mosiężna są okrągłe. Płytka P2 opiera się na trzech izolujących nóżkach.

Na początku glicerynę umieszczoną w termostacie podgrzewamy do temperatury 80 C. Po podgrzaniu wyłączamy grzałkę , jednocześnie włączając drugą , utrzymującą ustaloną temperaturę 80 C. Następnie podłączamy termoparę do cyfrowego miernika temperatury. Płytkę wybranego izolatora przeznaczoną do pomiaru przewodności cieplnej kładziemy na płycie P2 ( odbiornik ciepła ). Źródło ciepła P1 ( mosiężna puszka ) kładziemy na badanej płytce izolatora.

Taki układ płyt ogrzewamy do chwili ustalenia się temperatury T1 górnej płyty i temperatury T2 dolnej płyty , tj. T1-T2 = const. Ustalona wartośc temperatury odczytana na cyfr.mier.temp. nazywa się temperaturą różnicową. Ustalenie się tych temperatur zachodzi wówczas , gdy ilość ciepła przewodzona przez badaną płytkę jest równa ilości ciepła wypromieniowanej przez dolną płytę. Aby określić tę ilość ciepła , należy wyznaczyć szybkość stygnięcia dolnej płytki w pobliżu temperatury T2. W tym celu ,po wyjęciu badanej płytki , poprzez bezpośredni kontakt P1 i P2 ogrzewamy dolną płytę o 3 C od temperatury różnicowej , a następnie po zdjęciu puszki P1 wyznacza się szybkość jej stygnięcia. W jednostkowych odstępach czasu tj. co 30 s , mierzymy temperaturę T2 do chwili gdy będzie ona większa o około 4 C od temperatury równowagi.

Tr - 3 C < Tr < Tr + 4 C - przedział temperatur w którym mierzymy szybkośc stygnięcia.

2. WYNIKI POMIARÓW.

2.1 Płytka badanego izolatora.

LP.	2r1 [ mm ]	r1 r1 [ mm ]	d1 d1[ mm ]
1.	149,4	74,7 0,1	2,0 0,1
2.	149,3	74,7 0,1	2,1 0,1
3.	149,2	74,6 0,1	2,0 0,1
4.	149,3	74,7 0,1	2,1 0,1
5.	149,4	74,7 0,1	2,0 0,1
< średnie >	149,3	74,7 0,1	2,0 0,1

2.2 Płyta mosiężna ( P2 ).

m = ( 1669 0,2 ) g ; c (ciepło właściwe mosiądzu ) = ( 375 40 ) J / kg K

LP.	2r [ mm ]	r r [ mm ]	d d [ mm ]
1.	150,2	75,1 0,1	12,3 0,1
2.	150,1	75,1 0,1	12,1 0,1
3.	150,2	75,1 0,1	12,3 0,1
4.	150,2	75,1 0,1	12,2 0,1
5.	150,1	75,1 0,1	12,1 0,1
< średnie >	150,2	75,1 0,1	12,2 0,1

2.3 Temperatura różnicowa TR = T1 - T2 = 11C = const ( temperatura równowagi )

2.4 Szybkość stygnięcia w przedziale 8C < TR < 15C

LP.	t [ s ]	T [ C ]	T[ C ]	n [ C / s ]	n
1.	0	8,0
2.	30	8,3	0,3	0,01	0,023
3.	60	9,1	0,8	0,026	0,007
4.	90	10,1	1	0,03	0,003
5.	120	11,3	1,2	0,04	0,007
6.	150	12,5	1,2	0,04	0,007
7.	180	13,6	1,1	0,036	0,003
8.	210	14,8	1,2	0,04	0,007
9.	240	16,0	1,2	0,04	0,007

< n > = ( 0,033 0,008 ) C / s

2.5 Krzywa stygnięcia.

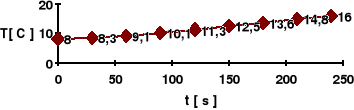
2.6 Współczynnik przewodnictwa cieplnego k.

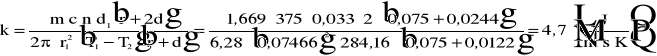
3.ANALIZA BŁĘDÓW.

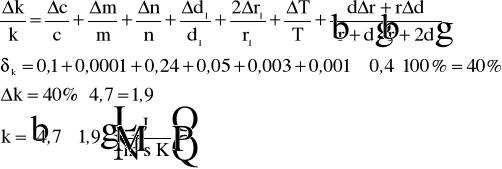
4.UWAGI I WNIOSKI.

Wzór na współczynnik przewodności cieplnej k wyprowadzono przy założeniu , że prąd ciepła jest normalny do powierzchni badanej płytki. Ponadto szybkość stygnięcia płytki ( mosiężnej ) w stanie stacjonarnym może być nieco różna od wyznaczonej doświadczalnie ze względu na większy wpływ prądów konwekcyjnych na stygnięcie powierzchni górnej płytki niż dolnej. Dodatkowo pewnym przybliżeniem jest także założenie proporcjonalności wypromieniowanego ciepła do wielkości powierzchni.

4.UWAGI I WNIOSKI.

Stosunkowo duży błąd k wynika z następujących faktów :

a) płytka izolatora wypromieniowuje ciepło również z brzegów ,

b) szybsze stygnięcie górnej powierzchni płytki mosiężnej spowodowane konwekcją ,

c) założenie proporcjonalności wypromieniowanego ciepła do powierzchni.

---