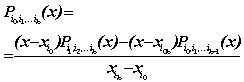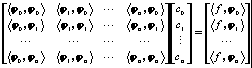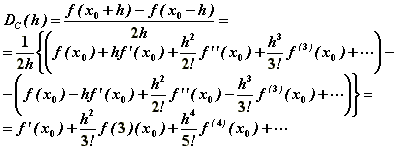1. Metody numeryczne (analiza numeryczna)Nauka zajmująca się rozwiązywaniem problemów matematycznych metodami arytmetycznymi sztuka doboru spośród wielu możliwych procedur takiej, która jest „najlepiej” dostosowana do rozwiązania danego zadania 2. Oszacowanie błędu numerycznego obliczenia ∫a^bf(x)dz przy n+1 obliczeniach wart. f(x); metoda trapezów: (b-a)^3f''(ε1)/12n^2; metoda Simpsona [(b-a)^5f^(4)(ξ2)]/180n^4 3. Błąd bezwzględny Δa=a^∼-a , błąd względny εa=Δa/a, ⇒ a^∼=Δa +a ⇒ εa=(a^∼/a)-1 4. Przenoszenie się błędu w obliczeniach numerycznych: y^∼=4.4, poprawnie zaokrąglona =4.35<y<4.45, |Δy|<0.05, |εy|<0.05/4.45, pie(y^∼)=2.0976, 2.0857<pie(y)<2.1095, |Δpie(y)|<0.0119, |εpie(y)|<0.0057, x^∼=10.3, poprawnie zaokrąglona 10.25<x<10.35, Δ i ε tak samo jak y, z^∼=ln(x^∼+pie(y^∼))=2.5175, 2.5125< ln(x+pie(y))<2.5275, Δ i ε tak samo. 5. Wykorzystanie podstawowych wzorów: x1,x^∼1,ε1 i x2,x^∼2,ε2 , iloczyn y=x1x2, εy=(x^∼1x^∼2)/( x1x2)-1=(1+ε1)(1-ε2)-1≈ε1+ε2 ; pierwiastek y=√x, εy=˝ε ; iloraz y=x1/x2, εy=ε1-ε2 ; suma y=x1±x2, εy=(x1ε1+x2ε2)/(x1±x2). 6. Metoda przybliżona: Δy=y(x1)-y(x), |Δy|=∑^n|(δy/δxi)(x)||Δxi| , |εy|=∑^n|(xiδy/yδxi)(x)||εxi| , 7. Aproksymacja liniowa średnio kwadratowa: funkcja przybliżana f(x), siatka węzłów xi, i=0,..m, fi=f(xi), dane: punkty węzłowe (xi,fi) i=0,..m , współczynniki wagowe wi>0 i=0,..m , funkcje bazowe ϕi(x) i=0,..n , funkcja aproksymująca , szukane stałe ci takie by Twierdzenie Jeżeli funkcje bazowe są liniowo niezależne to zadanie aproksymacji liniowej średniokwadratowej ma jedyne rozwiązanie. Rozwiązanie to spełnia układ równań normalnych: Jeżeli f. bazowe są rodziną f. ortogonalych to rozw. Upraszcza się 8. Wielomiany Czebyszewa Tn(x)=cos(narccos(x)) , -1≤x≤1, n=0,1,... ; T0(x)=1, Tn+1(x)=2xTn(x)-Tn-1(x). Współczynnik wiodący wielomianu Tn(x) jest równy 2^n-1 dla n=1,2,.., Tn(-x)=(-1)^nTn(x). Wielomian Tn+1(x) ma n+1 zer xk=cos[(2k+1)π/2(n+1)]. Układ wielomianów T0(x),..,Tn(x) jest ortogonalny względem wag wi=1 i węzłów xi, które są zerami wielom. Tn+1(x ) 9. Tw. Weierstrassa : Jeżeli f. f(x) jest ciągła w skończonym przedziale a,b to ∀ ε>0 ∃ P(x) stopnia n, taki że ∀ x∈(a,b) |f(x)-Pn(x)|<ε. 10. Interpolacja: Dla dowolnych, różnych n+1 p. węzłowych istnieje dokładnie jeden wielomian interpolacyjny stopnia co najwyżej n takie, że P(xi)=fi dla i=0,1,..,n. Wzór interpolacyjny Lagrange'a 11. Rekurencyjne tworzenie wielomianów interpolacyjnych: Wzór rekurencyjny Reszta wzoru interp. Jeżeli f() ma ciągłe poch. do rzędu n+1 a P() jest wielomianem interp. st. n to gdzie ξ jest pewnym p. z najmn. przedz. domkn. zawier. x, x0,..,xn.

12. Ekstrapolacja iterowana Richardsona: Do obliczenia pewnej wielkości stosuje się metodę numeryczną z parametrem h. Wynikiem jej działania jest F(h). Wartością dokładną jest F(0). Zakładamy, że znamy postać rozwinięcia (p1<p2<p3...): F(h)=a0+a1h^p1+..+anh^pn. F(0) ekstrapolujemy na podstawie kilku obliczonych wart. F(h0), F(q^-1h0), F(q^-2h0), F(q^-3h0)... q>1. Ekstrapolacja iterowana Richardsona pozwala na utworzenie ciągu f. F1(h),..,Fn(h), którego n-ty wyraz ma rozwinięcie Zastosowanie do różniczkowania numerycznego Różnica progresywna p1=1, p2=2, p3=3,... Różnica centralna : p1=2, p2=4, p3=6,... 13. Całkowanie numeryczne: Kwadratura: 14. Kwadratury Newtona-Cotesa: uzyskane przez interpolację wielomianem z węzłami równoodległymi: xi=a+ih, i=0,..,n , h=(b-a)/n fi=f(xi)=Pn(xi) ; kwadratury złożone xi=a+ih, i=0,..,n , h=(b-a)/n: wzór prostokątów : wzór trapezów: Oszacowanie błędu obcięcia: Metoda Romberga=złożona kwadratura trapezów+ekstrapolacja Richardsona q=2, pi=2i

---