STATYKA

1. Co to jest siła.

2. Omówic podstawowe prawa i aksjomaty statyki

3. Miara wektora i rzuty na osie

4. Przekształcenia elementarne

5. Warunki równowagi zbieżnego układu przestrzennego sił.

6. Moment siły względem osi i punktu.

7. Wykazać że moment pary sił jest niezależny od bieguna.

8.Do jakiego układu można zredukowac dowolny przestrzenny układ sił.

9. Wymienić szczególne przypadki redukcji dowolnego układu sił kiedy one wystąpią?

10. Warunki równowagi układu płaskiego

11. Stopień zmienności mechanizmu i różnica pomiędzy układem mechanicznym, a mechanizmem

12. Reakcje wewnętrzne

13. Metoda Rittera

14. Znane są współrzędne węzłów kratownicy

15. Położenie środka sił równoległych

16. Moment statyczny figury płaskiej względem osi

17. Tensor bezwładności18. Główne centralne osie bezwładności

19.

20. Warunkiem koniecznym i wystarczającym geometrycznej niezmienności układu złożonego z 3 tarcz

21. Wypadkowa

22.Wyznaczyć położenie siły wypadkowej układu

23. Co nazywamy osią środkową

KINEMATYKA

1. Przedstawić sposoby określania ruchu punktu?

2. Podąć związek miedzy wektorowym równaniem ruchu a równaniem we współrzędnych prostokątnych.

3. Jak określamy wektor prędkości średniej i chwilowej w ruchu krzywoliniowym

4. Określić współrzędne prędkości punktu gdy znane są równania ruchu we współrzędnych prostokątnych.

5. Co to jest wektor przyśpieszenia w ruchu krzywoliniowym.

6. Określic współrzędne przyśpieszenia punktu, gdy znane są jego równania ruchu we współrzędnych prostokątnych.

7. Podać właściwości pochodnej wektora jednostkowego.

8. Scharakteryzować przyspieszenie styczne i normalne punktu.

9. Co nazywamy hodografem prędkości, jaki jest jego związek z wektorem przyśpieszenia.

10. Jaki ruch ciała sztywnego nazywamy postępowym. Podać własności tego ruchu.

11. Zdefiniować ruch obrotowy wokół stałej osi.

12.Przytoczyć związek między prędkościa obrotową a prędkościa kątową

13. Jak wyznaczyć przyśpieszenie styczne i normalne punktów ciała w ruchu obrotowym.

14. Jaki ruch ciała nazywamy płaskim i jakie są jego równania

15. Co to jest chwilowy środek obrotu i jak go wyznaczamy

16. Podac zależność miedzy prędkościami dwóch punktów ciała w ruchu płaskim.

17. Zdefiniować ruchy: względny, unoszenia i bezwzględny, oraz prędkości w tych ruchach.

18. Zdefiniowac przyśpieszenia unoszenia, względne i przyśpieszenie Coriolisa.

19. Omówic własności przyśpieszenia Coriolisa

20. Jaki jest cel analizy kinetycznej mechanizmów

21. W oparciu o jakie twierdzenia wyznaczamy chwilowe położenia mechanizmu.

22. Oblicz pochodną
wektora który jest funkcją t przez inna funkcję s(t)

23. Oblicz pochodna iloczynu skalarnego dwóch wektorów

24. Co można powiedzieć o torach punktów ciała w ruchu obrotowym.

25. Podac podstawowe własności ruchu płaskiego.

26. Podac i opisac katy Eulera

DYNAMIKA

1.Jak wyznaczamy siłę działającą na P.M. jeżeli znany jest jego ruch

2.Jak wyznaczamy stałe całkowania w równaniach ruchu punktu

3.Jakie jest równanie ruchu harmonicznego drgań

4.Od czego zależy częstość drgań harmonicznych

5.Wyznaczyc czestość drgań masy m zawieszonej na układzie jak na rys.

6.W jaki sposób zmienia się amplituda drgań tłumionych

7.Co to jest dekrement tłumienia

8.co to jest praca elementarna

9.Jak obliczamy pracę siły na przemieszczeniu krzywoliniowym

10. Jak obliczamy pracę siły ciężkości w polu grawitacyjnym

11. Co to jest pole siły

12. Czemu równa jest praca w polu potencjalnym

13. w jaki sposób wyznaczamy siłę pola potencjalnego jeżeli znany jest jego potencjał

14. Podać i objaśnić twierdzenie o energii kinetycznej P.M

15. Podać zasadę zachowania całkowitej energii mechanicznej

16. Podać i uzasadnić twierdzenie o pędzie

17. Co to jest impuls (popęd) elementarny

18. jakie są skalarne równania określające twierdzenie o pędzie

19. Podać twierdzenie o kręcie P.M. względem punktu (osi)

20. Na czym polega zasada ruchu środka masy

21. jak obliczamy wektor pędu C.S

22. Podać sposób obliczania krętu c.s. poruszającego się ruchem postępowym, względem stałego punktu

23. Objaśnić ogólnie co to są reakcje dynamiczne łożysk osi stałej obracającego się c.s.

24. Kiedy pęd punktu jest wielkością stałą

25. Kiedy przyrost krętu względem Bieguna równa się zeru

26. Jak związane sa praca i energia mechaniczna w układzie izolowanym

27. Jaką powierzchnię nazywamy ekwipotencjalną

28. W jaki sposób sprawdzamy czy dane pole sił jest polem potencjalnym

29. Jak wyznaczamy energie potencjalna mając dane składowe sił potencjalnych30. Podać i objasnić zalezność energii kinetycznej PM. Od pracy sił działających na niego

Statyka

1. Co to jest siła.

Siła. Siły zdefiniować nie możemy, ale możemy ją zmierzyć poprzez pomiar skutków jej działania

(nadanie ciału przyspieszenia, lub w przypadku ciał odkształcalnych - jego deformację). Dla celów

praktycznych „definiujemy” siłę jako oddziaływanie jednego ciała na drugie. Oddziaływanie takie

może być realizowane na drodze bezpośredniego kontaktu tych ciał, lub na odległość (siły

grawitacji, magnetyczne, elektrostatyczne itp.).

2. Omówic podstawowe prawa i aksjomaty statyki

Zasada 1

Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy, gdy działają wzdłuż jednej prostej, są przeciwnie skierowane i mają te same wartości liczbowe.

Zasada 2

Działanie układu sił przyłożonych do ciała sztywnego nie ulegnie zmianie, gdy do tego układu zostanie dodany lub odjęty dowolny układ równoważących się sił (tzw. Układ zerowy). Interpretacja pierwszej zasady statyki Interpretacja drugiej zasady statyki Do ciała sztywnego zawsze można przyłożyć dwie równe co do wartości liczbowej i przeciwnie skierowane siły, działające wzdłuż tego samego kierunku. Zerowe układy sił wykorzystywane są do identyfikacji sił działających na elementy konstrukcyjne.

Z zasady 2 wypływa ważny praktyczny wniosek, że każdą siłę działającą na ciało sztywne można dowolnie przesuwać wzdłuż kierunku jej działania. Wektor, który może być dowolnie przesuwany wzdłuż kierunku działania, nazywa się wektorem przesuwnym. Siła działająca na ciało sztywne jest

wektorem swobodnym.

Zasada 3

Dowolne dwie siły P1 i P2 , przyłożone do jednego punktu,

można zastąpić siłą wypadkową R przyłożoną do tego punktu i przedstawioną jako wektor będący przekątną równoległoboku ABCD zbudowanego na wektorach sił w sposób pokazany na rysunku.

Zasada 4

Każdemu działaniu towarzyszy równe co do wartości i przeciwnie skierowane wzdłuż tej samej prostej

przeciwdziałanie.

Zasada 5

Każde ciało nieswobodne można myślowo oswobodzić od więzów, zastępując przy tym ich działanie odpowiednimi reakcjami. Dalej ciało to można rozpatrywać jako ciało swobodne, podlegające działaniu sił czynnych (obciążeń) oraz sił biernych (reakcji).

3. Miara wektora i rzuty na osie.

a=
-długość wektora

ax=a*cosα

ay=a*cos długości rzutów na osie układu współrzędnych.

az=a*cos

4. Przekształcenia elementarne

Przekształcenie elementarne α - usunięcie lub dołączenie do układu sił A układu złożonego z dwu wektorów przeciwnych leżących na jednej prostej tzn. układu sił.

Przekształcenie elementarne β lub dołączenie do układu sił A układu złożonego z kilku wektorów o wspólnym punkcie zaczepienia i o sumie równej wektorowi zerowemu tzn. układu sił.

Wykonując na układzie sił przekształcenie elementarne nie zmieniamy jego działania statycznego i dynamicznego.

5. Warunki równowagi zbieżnego układu przestrzennego sił.

W układzie sił wolno przesuwać siłę wzdłuż jej prostej działania.

W układzie sił wolno kilka sił o wspólnym punkcie zaczepienia zastapić ich sumą zaczepioną w tym punkcie.

W układzie sił wolno siłę rozłożyć na sumę kilku sił zaczepiając je w tym samym punkcie.

6. Moment siły względem osi i punktu.

Moment siły a zaczepionej w punkcie A względem punktu Q zwanego biegunem, rozumiemy wektor:

MQ= QA x a = r x a

MQ=0 gdy a=0 lub r=0, lub gdy prosta działania siły przechodzi przez Q.

Moment siły względem osi Z rozumiemy wektor M_Z = QA' x a_π

M_Z = 0 gdy a_π = 0 czyli gdy a\\Z lub gdy QA' = 0 czyli gdy prosta działania siły przecina oś Z.

7. Wykazać że moment pary sił jest niezależny od bieguna.

Przez parę sił rozumiemy układ dwu sił przeciwnych różnych od 0, których proste działania nie pokrywają się. Ponieważ suma tego układu jest równa zero to moment pary sił jest stały niezależny od bieguna.

8.Do jakiego układu można zredukowac dowolny przestrzenny układ sił. Dowolny przestrzenny układ sił możemy zredukować do:

• Skrętnika gdy R = a* M_Q =/ 0

• Wypadkowej gdy R=0 i a=/0

• Parze sił gdy R=0 a=0 M=/0

• Układowi zerowemu gdy R=0 a=0 M=0

R=a* M_Q

a= ∑a_i

M_Q = ∑OA* a_i

9. Wymienić szczególne przypadki redukcji dowolnego układu sił kiedy one wystąpią?

10. Warunki równowagi układu płaskiego

Układ sił nazywamy płaskim, jeżeli proste działania wszystkich sił układu leżą na jednej płaszczyźnie punktów zczepienia ewentualnych zerowych wektorów sił nie bierzemy pod uwage.

Pierwsze twierdzenie o redukcji:

Każdy układ płaski sił jest równoważny układowi dwu sił o prostych działania leżących w płaszczyźnie układu, których punkty zaczepienia możemy obrać dowolnie w płaszczyźnie układu.

Drugie twierdzenie o redukcji:

Dowolny układ sił jest równy układowi złożonego z sumy tego układu zaczepionej w dowolnie obranym punkcie oraz pary o momencie równym momentowi tego układu wglądem tego punktu.

11. Stopień zmienności mechanizmu i różnica pomiędzy układem mechanicznym, a mechanizmem

Przez układ mechaniczny ciał sztywnych rozumiemy zbiór skończony ciał sztywnych, które są ze sobą połączone za pomocą tak zwanych więzów wewnętrznych a z układem odniesienia są połączone więzami zewnętrznymi.

Stopień zmienności mechanizmu określamy poprzez liczbę posiadanych przez niego stopni swobody względem dowolnego płaskiego układu współrzędnych związanego nieruchomo z podłożem.

12. Reakcje wewnętrzne

Reakcje są to oddziaływania więzów ciała nieswobodnego i wyznaczmy je z warunków koniecznych i wystarczających o układach sił działających na ciało sztywne nieswobodne.

Warunek 1- suma sił czynnych i reakcyjnych musi być wektorem zerowym, oraz moment układu sił czynnych i reakcyjnych musi być wektorem zerowym.

Warunek 2- momenty wszystkich sił czynnych i reakcyjnych względem trzech biegunów muszą być wektorami zerowymi.

Reakcje wewnętrzne są to siły wzajemnego oddziaływania ciał i jako takie tworzą układ sił przeciwnych leżących na jednej prostej.

13. Metoda Rittera wyznaczania siły w pręcie polega na przecięciu kratownicy przez trzy nie równoległe i nie przecinających się w jednym punkcie pręty, wśród tych prętów musi się znajdować interesujący nas pręt. W metodzie tej wykorzystujemy trzy równania równowagi (układ płaski Sx=0 , Sy=0 , Mq=0).

14. Znane są współrzędne węzłów kratownicy

15. Położenie środka sił równoległych

Położenie punktu C zależy od modułów wektorów a_i i położenia ich punktów alokacji A_i.

16. Moment statyczny figury płaskiej względem osi jest równy iloczynowi powierzchni tej figury i odległości jej środka od osi. Moment statyczny względem osi przechodzącej przez środek figury jest równy 0.

S_x = A_i * y_i S_y = A_i * x_i

17. Tensor bezwładności wyznaczamy ze wzrou:

T' = R * T * R^T

18. Główne centralne osie bezwładności

Zawsze istnieją dwie wzajemnie prostopadłe osie x₁ i x₂ względem, których moment dewiacji I_xy jest równy 0. Osie te noszą nazwę osi głównych bezwładności. Jeżeli figura ta ma oś symetrii to jest ona jedną z głównych osi bezwładności tej figury. Na tej osi leży też środek geometryczny - jest więc główną centralną osią bezwładności.

19.

20. Warunkiem koniecznym i wystarczającym geometrycznej niezmienności układu złożonego z 3 tarcz jest V≤0 , oraz punkty przecięć kierunków par prętów między tarczami nie mogą leżeć na jednej prostej.

Układ tarcz jest geometrycznie niezmiennym jeśli można go zastąpić jedną tarczą. Trzy tarcze wzajemnie połączone za pomocą przegubów tworzących trójkąt są układem wewnętrznie geometrycznie niezmiennym.

21. Wypadkowa jest to wektor równy sumie wektorów, który równoważy układ, zastępuje cały układ, jest ściśle związany z pewnym punktem.

Suma układu sił jest to wektor swobodny.

22.Wyznaczyć położenie siły wypadkowej układu:

23. Osią środkową nazywamy miejsce geometryczne punktów względem, których wektor momentu układu jest równoległym do wektora sumy lub równa się 0.

Jeżeli istnieje wypadkowa to istnieje oś środkowa.

Kinematyka

1. Przedstawić sposoby określania ruchu punktu?

Ruch punktu w dowolnej chwili t określić można za pomocą równań ruchu:

1. x₁= x₁(t) x₂= x₂(t) x₃= x₃(t)

2. ρ= ρ(t) γ= γ(t) x₃= x₃(t)

3. r= r(t) γ= γ(t) υ= υ(t)

2. Podąć związek miedzy wektorowym równaniem ruchu a równaniem we współrzędnych prostokątnych.

Zarówno równanie wektorowe ruchu, jak i równania we współrzędnych prostokątnych są opisane jako funkcję czasu.

Współrzędne prostokątne Równanie wektorowe

r_x=x(t) r= r(t)= r(x(t), y(t), z(t))

r_y=y(t)

r_z=z(t)

3. Jak określamy wektor prędkości średniej i chwilowej w ruchu krzywoliniowym

Wektor prędkości średniej jest ilorazem wektora wodzącego ∆ r¯ przez przyrost czasu ∆t.

Prędkość chwilowa jest pochodną względem czasu wektora wodzącego

V= lim
=

∆t→0

4. Określić współrzędne prędkości punktu gdy znane są równania ruchu we współrzędnych prostokątnych.

Gdy znane są równania ruchu we współrzędnych prostokątnych to współrzędne prędkości punktu są jego pochodnymi względem czasu t.

x₁= x₁(t) V_x1=
=

x₂= x₂(t) V_x2=
=

x₃= x₃(t) V_x3=
=

5. Co to jest wektor przyśpieszenia w ruchu krzywoliniowym.

Jest punkt P w chwili t zajmuje położenia A natomiast w chwili t+∆t położenie B, to granica

lim

jest wektor przyśpieszenia w chwili t i jest on styczny do hodografu predkości.

∆t→0

6. Określic współrzędne przyśpieszenia punktu, gdy znane są jego równania ruchu we współrzędnych prostokątnych.

Współrzędne przyśpieszenia są drugimi pochodnymi względem czasu t, po współrzędnych prostokątnych opisujących ruch.

7. Podać właściwości pochodnej wektora jednostkowego.

Pochodna wektora jednostkowego, jest prostopadła do tego wektora lub wersora tego wektora.

8. Scharakteryzować przyspieszenie styczne i normalne punktu.

- przyśpieszenie styczne, ma ten sam kierunek co wektor prędkości (jest styczny do toru ruchu) nie wystepuje w ruchu po okręgu, gdyż prędkość kątowa jest stała ω=const

- przyśpieszenie normalne jest to wektor leżący w płaszczyźnie ruchu i ma kierunek promienia krzywizny, a zwrot zawsze przeciwny, skierowany ku środkowi krzywizny, czyli normalny (prostopadły do toru)

9. Co nazywamy hodografem prędkości, jaki jest jego związek z wektorem przyśpieszenia.

Hodografem nazywamy krzywą, która zakreśla punkt w czasie ruchu. Wektor przyśpieszenia w chwili t jest styczny do hodografu prędkości.

10. Jaki ruch ciała sztywnego nazywamy postępowym. Podać własności tego ruchu.

Ruch bryły nazywamy postępowym, jeżeli dowolna prosta związana z bryłą pozostaje w czasie ruchu stale do siebie równoległa.

Własności ruchu postępowego:

-wszystkie punkty bryły poruszającej się ruchem postępowym

-mają jednakową prędkość
i jednakowe przyśpieszenie
.

11. Zdefiniować ruch obrotowy wokół stałej osi.

Ruch obrotowy wokół stałej osi jest to ruch dowolny punktu bryły po torze w kształcie okręgu, o którym będą decydowały: prędkość kątowa ω i przyśpieszenie kątowe є. W ruchu rym musi być zawsze położenie osi.

12.Przytoczyć związek między prędkościa obrotową a prędkościa kątową

Prędkość kątowa jest stała dla każdego punktu bryły, natomiast prędkość obrotowa każdego punktu zależy od odległości od osi obrotu bryły

=

13. Jak wyznaczyć przyśpieszenie styczne i normalne punktów ciała w ruchu obrotowym.

Przyśpieszenie punktu M ma dwie składowe

składowa
ma kierunek styczny do toru K (podobnie jak prędkość) nosi nazwę przyśpieszenia stycznego.

=

składowa
ma kierunek prostopadły do
i
jest skierowana do osi l, przecina ją pod kątem prostym nazywana jest przyśpieszeniem dośrodkowym

=

14. Jaki ruch ciała nazywamy płaskim i jakie są jego równania

Ruch płaski bryły jest wówczas, gdy jej punkty poruszają się w płaszczyznach równoległych do siebie.

15. Co to jest chwilowy środek obrotu i jak go wyznaczamy

Jeżeli znane są wektory V_a i V_b punktów A i B tarczy to punkt C lezy w punkcie przecięcia prostopadłych V_a i V_b . Punkt C nosi nazwę chwilowego środka obrotu.

16. Podac zależność miedzy prędkościami dwóch punktów ciała w ruchu płaskim.

V_m=V_A+V^(A)_M, V^(A)_M- prędkość punktu względem punktu A

V^(A)_M=

|V^(A)_M|= ωq

Twierdzenie ( o prędkościach prędkościach ruchu płaskim).

Prędkość punktu M w ruchu plaskim można przedstawic jako sumę prędkości dowolnie wybranego bieguna O i prędkość punktu M w ruchu obrotowym wokół tego bieguna tzn

17. Zdefiniować ruchy: względny, unoszenia i bezwzględny, oraz prędkości w tych ruchach.

ruch unoszenia- jest to ruch ciała, po którym porusza się rozpatrywany punkt

ruch względny- jest to ruch punktu względem bryły będącej w ruchu

ruch bezwzględny - jest to ruch punktu względem nieruchomego układu V=V_u+V_W

18. Zdefiniowac przyśpieszenia unoszenia, względne i przyśpieszenie Coriolisa.

Przyśpieszenie Coriolisa-nosi nazwę przyśpieszenia dewiacyjnego i pochodzi od obrotu układu względnego.

= 2

Przyśpieszenie unoszenia jest to przyśpieszenie tego punktu układu ruchomego względem układu stałego, który w danej chwili pokrywa się z punktem poruszającym się

Przyśpieszenie względne jest równe przyśpieszeniu normalnemu ponieważ, jest to ruch ze stałą prędkością

19. Omówic własności przyśpieszenia Coriolisa.

Przyśpieszenie Coriolisa
staje się zerem, gdy ruch tego układu jest ruchem postępowym (
= 0)

20. Jaki jest cel analizy kinetycznej mechanizmów

Celem analizy kinetycznej mechanizmów jest ustalenie położenia układu po nadaniu jednemu z jego prętów pewnej prędkości. Dzieki niemu jestemy w stanie ustalic przemieszczenie każdego punktu układu

21. W oparciu o jakie twierdzenia wyznaczamy chwilowe położenia mechanizmu.

Chwilowe położenia mechanizmu wyznaczamy w opraciu o przesuniecia możliwe układu, czyli zespół nieskończenie małych przesunieć punktów układu

, oraz o możliwe prędkości układu gdy (3T-a>0)
,
= 1,2,...,a

22. Oblicz pochodną
wektora który jest funkcją t przez inna funkcję s(t)

23. Oblicz pochodna iloczynu skalarnego dwóch wektorów
i

24. Co można powiedzieć o torach punktów ciała w ruchu obrotowym.

Torami punktów ciała w ruchu obrotowym są koła położone w płaszczyznach prostopadłych do osi obrotu i środkach leżących na tej osi. Promienie wspomnianych kół równe są odległościom punktów od osi obrotu.

25. Podac podstawowe własności ruchu płaskiego.

1) w ruchu płaskim wektory prędkości kątowej
i przyśpieszenia kątowego
są kolinearne, prostopadłe do płaszczyny kierującej.

2) prędkość punktu w ruchu płaskim można przedstawic jako sumę prędkości dowolnie wybranego bieguna i prędkości punktu w ruchu obrotowym wokół tego bieguna.

3) przyśpieszenie punktu w ruchu płaskim można przestawic jako sumę przyśpieszeń dowolnie wybranego bieguna i przyśpieszenia punktu w ruchu wokół tego bieguna.

26. Podac i opisac katy Eulera

,
- kąty Eklera

- kąt nutacji - odchylenia osi
od z

- kąt precesji - odchylenia osi węzłów od osi x

-kąt obrotu własnego -odchylenie osi
od osi węzłów w ∏

Dynamika

1.Jak wyznaczamy siłę działającą na P.M. jeżeli znany jest jego ruch:

Wyznaczamy z równań dynamicznych ruchu

ma_x=P_x , ma_y=P_y , ma_z=P_z

2.Jak wyznaczamy stałe całkowania w równaniach ruchu punktu:

Podstawiając warunki początkowe do równań na V, a i tor ruchu

3.Jakie jest równanie ruchu harmonicznego drgań:

x''+2*Ex'+
* x =0 ; 2*E=c/m ;
=k/m

4.Od czego zależy częstość drgań harmonicznych:

Zależy od masy i współczynnika sprężystości k

5.Wyznaczyc czestość drgań masy m zawieszonej na układzie jak na rys.

6.W jaki sposób zmienia się amplituda drgań tłumionych:

7.Co to jest dekrement tłumienia:

Dekrement tłumienia charakteryzuje tłumienie drgań

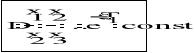
8.co to jest praca elementarna siły:

jest to iloczyn skalarny siły P oraz przyrostu wektora wodzącego r ; δL=P* Δr

9.Jak obliczamy pracę siły na przemieszczeniu krzywoliniowym:

Dzielimy przemieszczenie na elementarne części, liczymy pracę wyznaczając granicę dla n części dążące do nieskończoności, a długość l każdej część dążącą do 0

10. Jak obliczamy pracę siły ciężkości w polu grawitacyjnym

11. Co to jest pole siły

Pole sił jest to część przestrzeni która posiada te własności, że gdziekolwiek w niej umieścimy P.M. to zawsze działa na niego ściśle określona siła zależna tylko od położenia pktu.

12. Czemu równa jest praca w polu potencjalnym:

Praca wykonana na dowolnym przemieszczeniu od A(x1,y1,z1) do B(x2,y2,z2) jest równa różnicy potencjałów; L=U_B-U_A=U₂-U₁

13. w jaki sposób wyznaczamy siłę pola potencjalnego jeżeli znany jest jego potencjał:

V=całka f(r)dr

14. Podać i objaśnić twierdzenie o energii kinetycznej P.M.

Przyrost energii kinetycznej jest równy pracy w danym czasie

15. Podać zasadę zachowania całkowitej energii mechanicznej

Energia mechaniczna jest stała i równa się sumie energii potencjalnej i kinetycznej w dowolnym punkcie ruchu

16. Podać i uzasadnić twierdzenie o pędzie:

Iloczyn wektora prędkości v przez masę m nazywamy pędem P=V*m; mx''_i=P _i

Mdx _i'=P _i dt

17. Co to jest impuls (popęd) elementarny

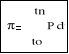
18. jakie są skalarne równania określające twierdzenie o pędzie

mx'_i(tn)-mx'_i(to)=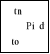

19. Podać twierdzenie o kręcie P.M. względem punktu (osi)

Moment pędu względem Bieguna 0 nosi nazwę krętu P.M. względem tego bieguna

20. Na czym polega zasada ruchu środka masy

Środek porusza się jak swobodny punkt materialny o masie równej masie układu pod działaniem sumy geometrycznej sił czynnych i reakcji

21. jak obliczamy wektor pędu C.S

p=v*m ; p={mx₁', mx₂', mx₃'}

22. Podać sposób obliczania krętu c.s. poruszającego się ruchem postępowym, względem stałego punktu

K'=Mo ; d/dt(r x mv)=r x P

23. Objaśnić ogólnie co to są reakcje dynamiczne łożysk osi stałej obracającego się c.s.

H'i=Pi+Rai+Rbi i=x,y,z

K'i=Mi(p)+Mi(r)

24. Kiedy pęd punktu jest wielkością stałą

Jeżeli siła czynna działająca na P.M. jest równa zeru to pęd P.M. jest stały

25. Kiedy przyrost krętu względem Bieguna równa się zeru

Jeżeli położenie P.M. od bieguna jest stałe

26. Jak związane sa praca i energia mechaniczna w układzie izolowanym

Praca siły czynnej działającej na P.M. w polu potencjalnym w danym przedziale czasu jest równa przyrostowi energii mechanicznej w tym przedziale

27. Jaką powierzchnię nazywamy ekwipotencjalną

Równego potencjału - tzn. powierzchnie w polu grawitacyjnym której wszystkie punkty mają równy potencjał

28. W jaki sposób sprawdzamy czy dane pole sił jest polem potencjalnym

WKW Potencjalności pola jest jest aby w danym polu praca po każdej drodze zamkniętej była zerem

29. Jak wyznaczamy energie potencjalna mając dane składowe sił potencjalnych jako funkcje współrzędnych pola

Ls=cał. Pi dxi=cał. (Pxdx+Pydy+Pzdz)=U1-U2

Lab=Ep1-Ep2

30. Podać i objasnić zalezność energii kinetycznej PM. Od pracy sił działających na niego:

Jeśli siła posiada potencjał to praca takiej siły na pewnym przesunięciu jest równa różnicy potencjałów i nie zależy od kształtu drogi toru ani od czasu

L=U_A-U_B = -[Ep_B-Ep_A]= - ΔEp

L= ΔEk= ΔEk-Ls= ΔEk+ ΔEp

---