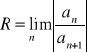Mówimy, że szereg![]()
jest zbieżny w punkcie z0 є A, jeżeli szereg liczbowy ![]()
jest zbieżny.
Szeregi funkcyjne i potęgowe
Szereg zbieżny
Mówimy, że szereg![]()
jest zbieżny w punkcie z0 є A, jeżeli szereg liczbowy ![]()
jest zbieżny.
Szereg rozbieżny
Mówimy, że szereg![]()
jest zbieżny (jednostajnie zbieżny) w zbiorze A, jeżeli ciąg sum cząstkowych tego szeregu: ![]()
jest zbieżny (jednostajnie zbieżny) w zbiorze A.
Kryterium Weierstrassa
Szereg ![]()
jest jednostajnie zbieżny w zbiorze A, jeżeli każda z funkcji uk(z) jest ograniczona w zbiorze A taką liczbą nieujemną ak, że szereg liczbowy ![]()
jest zbieżny.
Kryterium Dirichleta.
Szereg ![]()
jest zbieżny (jednostajnie zbieżny) w zbiorze A, jeżeli są spełnione dwa warunki:
ciąg {bk} liczb nieujemnych bk dąży monotonicznie do zera
ciąg funkcyjny ![]()
jest ograniczony (jednostajnie ograniczony) w zbiorze A.
Twierdzenie Cauchy-Hadamarda.
Promień zbieżności szeregu potęgowego wyraża się wzorem:
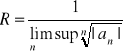
Oraz wzrór na podstawie kryterium d'Alemberta